Алгоритм Брезенхэма для построения линий

Алгоритм рисования линий

Алгоритм Брезенхэма — это алгоритм рисования линий , который определяет точки n -мерного растра , которые следует выбрать для формирования близкого приближения к прямой линии между двумя точками . Он обычно используется для рисования примитивов линий в растровом изображении (например, на экране компьютера ), поскольку он использует только целочисленное сложение, вычитание и сдвиг битов , все из которых являются очень дешевыми операциями в исторически распространенных компьютерных архитектурах. Это алгоритм инкрементной ошибки и один из самых ранних алгоритмов, разработанных в области компьютерной графики . Расширение исходного алгоритма, называемое алгоритмом средней точки окружности, может использоваться для рисования окружностей .

Хотя такие алгоритмы, как алгоритм Ву, также часто используются в современной компьютерной графике, поскольку они могут поддерживать сглаживание , линейный алгоритм Брезенхэма по-прежнему важен из-за своей скорости и простоты. Алгоритм используется в оборудовании, таком как плоттеры , и в графических чипах современных видеокарт . Его также можно найти во многих программных графических библиотеках . Поскольку алгоритм очень прост, он часто реализуется либо в прошивке , либо в графическом оборудовании современных видеокарт .

Сегодня название «Брезенхэм» используется для семейства алгоритмов, расширяющих или модифицирующих исходный алгоритм Брезенхэма.

История

Алгоритм Брезенхэма назван в честь Джека Элтона Брезенхэма, который разработал его в 1962 году в IBM . В 2001 году Брезенхэм написал: ^[1]

Я работал в вычислительной лаборатории в лаборатории разработки IBM в Сан-Хосе. Плоттер Calcomp был подключен к IBM 1401 через консоль пишущей машинки 1407. [Алгоритм] был в производственном использовании к лету 1962 года, возможно, месяцем или около того ранее. Программы в те дни свободно обменивались между корпорациями, поэтому у Calcomp (Джим Ньюленд и Кэлвин Хефте) были копии. Когда я вернулся в Стэнфорд осенью 1962 года, я поместил копию в библиотеку вычислительного центра Стэнфорда. Описание процедуры рисования линий было принято для презентации на национальном съезде ACM 1963 года в Денвере, штат Колорадо. Это был год, когда не было опубликовано никаких трудов, только повестка дня докладчиков и темы в выпуске Communications of the ACM. После того, как я сделал свою презентацию, человек из IBM Systems Journal спросил меня, могут ли они опубликовать статью. Я с радостью согласился, и они напечатали ее в 1965 году.

Метод

Иллюстрация результата линейного алгоритма Брезенхэма. (0,0) находится в верхнем левом углу сетки, (1,1) находится в верхнем левом конце линии, а (11, 5) находится в нижнем правом конце линии.

Будут использоваться следующие условные обозначения:

• верхний левый угол равен (0,0), так что координаты пикселей увеличиваются в направлениях вправо и вниз (например, пиксель в точке (7,4) находится прямо над пикселем в точке (7,5)), и
• Центры пикселей имеют целочисленные координаты.

Конечными точками линии являются пиксели и , где первая координата пары — столбец, а вторая — строка. ${\displaystyle (x_{0},y_{0})}$ ${\displaystyle (x_{1},y_{1})}$

Алгоритм будет первоначально представлен только для октанта , в котором сегмент идет вниз и вправо ( и ), а его горизонтальная проекция длиннее вертикальной проекции (линия имеет положительный наклон меньше 1). В этом октанте для каждого столбца x между и существует ровно одна строка y (вычисленная алгоритмом), содержащая пиксель линии, в то время как каждая строка между и может содержать несколько растеризованных пикселей. ${\displaystyle x_{0}\leq x_{1}}$ ${\displaystyle y_{0}\leq y_{1}}$ ${\displaystyle x_{1}-x_{0}}$ ${\displaystyle y_{1}-y_{0}}$ ${\displaystyle x_{0}}$ ${\displaystyle x_{1}}$ ${\displaystyle y_{0}}$ ${\displaystyle y_{1}}$

Алгоритм Брезенхэма выбирает целое число y, соответствующее центру пикселя , который ближе всего к идеальному (дробному) y для того же x ; в последовательных столбцах y может оставаться тем же самым или увеличиваться на 1. Общее уравнение линии, проходящей через конечные точки, задается следующим образом:

${\displaystyle {\frac {y-y_{0}}{y_{1}-y_{0}}}={\frac {x-x_{0}}{x_{1}-x_{0}}}}$.

Поскольку нам известен столбец x , строка пикселя y определяется путем округления этой величины до ближайшего целого числа:

${\displaystyle y={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}(x-x_{0})+y_{0}}$.

Наклон зависит только от координат конечной точки и может быть рассчитан заранее, а идеальный y для последовательных целочисленных значений x может быть рассчитан, начиная с наклона и многократно его добавляя. ${\displaystyle (y_{1}-y_{0})/(x_{1}-x_{0})}$ ${\displaystyle y_{0}}$

На практике алгоритм не отслеживает координату y, которая увеличивается на m = ∆y/∆x каждый раз, когда x увеличивается на единицу; он сохраняет границу ошибки на каждом этапе, которая представляет собой отрицательное значение расстояния от (a) точки, где линия выходит из пикселя, до (b) верхнего края пикселя. Это значение сначала устанавливается равным (из-за использования координат центра пикселя) и увеличивается на m каждый раз, когда координата x увеличивается на единицу. Если ошибка становится больше 0,5 , мы знаем, что линия переместилась вверх на один пиксель, и что мы должны увеличить нашу координату y и перенастроить ошибку, чтобы она представляла расстояние от верха нового пикселя, что делается путем вычитания единицы из ошибки. ^[2] ${\displaystyle y_{0}-0.5}$

Вывод

Чтобы вывести алгоритм Брезенхэма, необходимо сделать два шага. Первый шаг — преобразовать уравнение линии из типичной формы наклон-пересечение в нечто иное; а затем использовать это новое уравнение для рисования линии, основанной на идее накопления ошибок.

Уравнение линии

у=f(x)=.5x+1 или f(x,y)=x-2y+2=0

Положительные и отрицательные полуплоскости

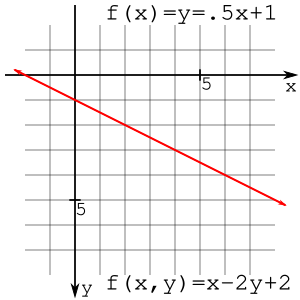
Форма наклона-пересечения прямой записывается как

${\displaystyle y=f(x)=mx+b}$

где — наклон, а — y-пересечение. Поскольку это функция только , она не может представлять вертикальную линию. Поэтому было бы полезно записать это уравнение как функцию и , чтобы иметь возможность рисовать линии под любым углом. Угол (или наклон) линии можно определить как «подъем над пробегом» или . Затем, используя алгебраические манипуляции, ${\displaystyle m}$ ${\displaystyle b}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle \Delta y/\Delta x}$

${\displaystyle {\begin{aligned}y&=mx+b\\y&={\frac {\Delta y}{\Delta x}}x+b\\(\Delta x)y&=(\Delta y)x+(\Delta x)b\\0&=(\Delta y)x-(\Delta x)y+(\Delta x)b\end{aligned}}}$

Позволяя этому последнему уравнению быть функцией и , его можно записать как ${\displaystyle x}$ ${\displaystyle y}$

${\displaystyle f(x,y):=Ax+By+C=0}$

где константы

• ${\displaystyle A=\Delta y=y_{1}-y_{0}}$
• ${\displaystyle B=-\Delta x=-(x_{1}-x_{0})}$
• ${\displaystyle C=(\Delta x)b=(x_{1}-x_{0})b}$

Затем линия определяется для некоторых констант , , и в любом месте . То есть для любого не на линии, . Эта форма включает только целые числа, если и являются целыми числами, поскольку константы , , и определены как целые числа. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle f(x,y)=0}$ ${\displaystyle (x,y)}$ ${\displaystyle f(x,y)\neq 0}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C}$

В качестве примера, линия тогда это можно записать как . Точка (2,2) находится на линии ${\textstyle y={\frac {1}{2}}x+1}$ ${\displaystyle f(x,y)=x-2y+2}$

${\displaystyle f(2,2)=x-2y+2=(2)-2(2)+2=2-4+2=0}$

и точка (2,3) не находится на прямой

${\displaystyle f(2,3)=(2)-2(3)+2=2-6+2=-2}$

и ни одна из точек (2,1)

${\displaystyle f(2,1)=(2)-2(1)+2=2-2+2=2}$

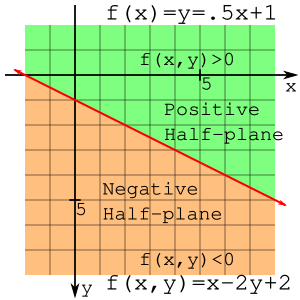
Обратите внимание, что точки (2,1) и (2,3) находятся на противоположных сторонах линии и оцениваются как положительные или отрицательные. Линия делит плоскость на две половины, и полуплоскость, которая имеет отрицательное значение, можно назвать отрицательной полуплоскостью, а другую половину можно назвать положительной полуплоскостью. Это наблюдение очень важно в оставшейся части вывода. ${\displaystyle f(x,y)}$ ${\displaystyle f(x,y)}$

Алгоритм

Начальная точка находится на линии

${\displaystyle f(x_{0},y_{0})=0}$

только потому, что линия определена как начинающаяся и заканчивающаяся в целочисленных координатах (хотя вполне разумно захотеть нарисовать линию с нецелочисленными конечными точками).

Точка-кандидат (2,2) синего цвета и две точки-кандидата зеленого цвета (3,2) и (3,3)

Имея в виду, что наклон не более , теперь возникает проблема, должна ли следующая точка быть в или . Возможно, интуитивно, точку следует выбирать на основе того, какая из них ближе к линии в . Если она ближе к первой, то включите первую точку в линию, если ко второй, то последнюю. Чтобы ответить на этот вопрос, оцените функцию линии в средней точке между этими двумя точками: ${\displaystyle 1}$ ${\displaystyle (x_{0}+1,y_{0})}$ ${\displaystyle (x_{0}+1,y_{0}+1)}$ ${\displaystyle x_{0}+1}$

${\displaystyle f(x_{0}+1,y_{0}+{\tfrac {1}{2}})}$

Если значение этого положительно, то идеальная линия находится ниже средней точки и ближе к точке-кандидату ; т.е. координата y должна увеличиваться. В противном случае идеальная линия проходит через среднюю точку или выше нее, а координата y должна оставаться прежней; в этом случае выбирается точка. Значение функции линии в этой средней точке является единственным фактором, определяющим, какую точку следует выбрать. ${\displaystyle (x_{0}+1,y_{0}+1)}$ ${\displaystyle (x_{0}+1,y_{0})}$

На соседнем изображении показана синяя точка (2,2), выбранная на линии с двумя зелеными точками-кандидатами (3,2) и (3,3). Черная точка (3, 2.5) является средней точкой между двумя точками-кандидатами.

Алгоритм целочисленной арифметики

В качестве альтернативы можно использовать разницу между точками вместо оценки f(x,y) в средних точках. Этот альтернативный метод допускает арифметику только с целыми числами, что обычно быстрее, чем использование арифметики с плавающей точкой. Чтобы получить другой метод, определите разницу следующим образом:

${\displaystyle D_{i}=f(x_{i}+1,y_{i}+{\tfrac {1}{2}})-f(x_{0},y_{0})}$

Для первого решения эта формулировка эквивалентна методу средней точки, поскольку в начальной точке. Упрощение этого выражения дает: ${\displaystyle f(x_{0},y_{0})=0}$

${\displaystyle {\begin{array}{rclcl}D_{0}&=&\left[A(x_{0}+1)+B\left(y_{0}+{\frac {1}{2}}\right)+C\right]&-&\left[Ax_{0}+By_{0}+C\right]\\&=&\left[Ax_{0}+By_{0}+C+A+{\frac {1}{2}}B\right]&-&\left[Ax_{0}+By_{0}+C\right]\\&=&A+{\frac {1}{2}}B=\Delta y-{\frac {1}{2}}\Delta x\end{array}}}$

Так же, как и в случае метода средней точки, если положительно, то выбираем , в противном случае выбираем . ${\displaystyle D_{0}}$ ${\displaystyle (x_{0}+1,y_{0}+1)}$ ${\displaystyle (x_{0}+1,y_{0})}$

Если выбрано , то изменение будет следующим: ${\displaystyle (x_{0}+1,y_{0})}$ ${\displaystyle D_{i}}$

${\displaystyle {\begin{array}{lclcl}\Delta D&=&f(x_{0}+2,y_{0}+{\tfrac {1}{2}})-f(x_{0}+1,y_{0}+{\tfrac {1}{2}})&=&A&=&\Delta y\\\end{array}}}$

Если выбрано , то изменение будет следующим: ${\displaystyle (x_{0}+1,y_{0}+1)}$ ${\displaystyle D_{i}}$

${\displaystyle {\begin{array}{lclcl}\Delta D&=&f(x_{0}+2,y_{0}+{\tfrac {3}{2}})-f(x_{0}+1,y_{0}+{\tfrac {1}{2}})&=&A+B&=&\Delta y-\Delta x\end{array}}}$

Если новый D положительный, то выбирается, в противном случае . Это решение можно обобщить, накапливая ошибку в каждой последующей точке. ${\displaystyle (x_{0}+2,y_{0}+1)}$ ${\displaystyle (x_{0}+2,y_{0})}$

Построение линии от (0,1) до (6,4), показывающей график линий сетки и пикселей

Все выводы для алгоритма сделаны. Одна из проблем производительности — это фактор 1/2 в начальном значении D. Поскольку все это касается знака накопленной разницы, то все можно умножить на 2 без каких-либо последствий.

В результате получается алгоритм, использующий только целочисленную арифметику.

plotLine(x0, y0, x1, y1) дх = х1 - х0 dy = y1 - y0 D = 2*dy - dx у = у0 для x от x0 до x1 график(x, y) если D > 0 у = у + 1 Д = Д - 2*дх конец, если Д = Д + 2*ди

Выполнение этого алгоритма для интервала от (0,1) до (6,4) дает следующие различия при dx=6 и dy=3: ${\displaystyle f(x,y)=x-2y+2}$

Д=2*3-6=0Цикл от 0 до 6 * x=0: график(0, 1) , D≤0: D=0+6=6 * x=1: график(1, 1) , D>0: D=6-12=-6, y=1+1=2, D=-6+6=0 * x=2: график(2, 2) , D≤0: D=0+6=6 * x=3: график(3, 2) , D>0: D=6-12=-6, y=2+1=3, D=-6+6=0 * x=4: график(4, 3) , D≤0: D=0+6=6 * x=5: график(5, 3) , D>0: D=6-12=-6, y=3+1=4, D=-6+6=0 * x=6: график(6, 4) , D≤0: D=0+6=6

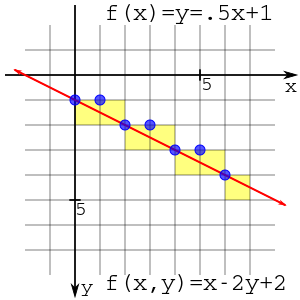
Результат этого графика показан справа. График можно просмотреть, построив график на пересечении линий (синие круги) или заполнив пиксельные поля (желтые квадраты). Независимо от этого, график тот же самый.

Все случаи

Однако, как упоминалось выше, это работает только для нулевого октанта , то есть линий, начинающихся в начале координат с наклоном от 0 до 1, где x увеличивается ровно на 1 за итерацию, а y увеличивается на 0 или 1.

Алгоритм можно расширить для охвата наклонов от 0 до -1, проверив, нужно ли увеличивать или уменьшать y (т.е. dy < 0).

plotLineLow(x0, y0, x1, y1) дх = х1 - х0 dy = y1 - y0 yi = 1 если dy < 0 yi = -1 ди = -ди конец, если D = (2 * dy) - dx у = у0 для x от x0 до x1 график(x, y) если D > 0 у = у + уи D = D + (2 * (dy - dx)) еще Д = Д + 2*ди конец, если

Поменяв местами оси x и y, можно записать реализацию для положительных или отрицательных крутых склонов как

plotLineHigh(x0, y0, x1, y1) дх = х1 - х0 dy = y1 - y0 кси = 1 если dx < 0 кси = -1 дх = -дх конец, если D = (2 * dx) - dy х = х0 для y от y0 до y1 график(x, y) если D > 0 х = х + кси D = D + (2 * (dx - dy)) еще Д = Д + 2*дх конец, если

Полное решение должно определять, x1 > x0 или y1 > y0, и менять входные координаты местами перед рисованием, таким образом:

plotLine(x0, y0, x1, y1) если abs(y1 - y0) < abs(x1 - x0) если x0 > x1 plotLineLow(x1, y1, x0, y0) еще plotLineLow(x0, y0, x1, y1) конец если  иначе  если y0 > y1 plotLineHigh(x1, y1, x0, y0) еще plotLineHigh(x0, y0, x1, y1) конец, если  конец, если

В низкоуровневых реализациях, которые обращаются к видеопамяти напрямую, особые случаи вертикальных и горизонтальных линий обычно обрабатываются отдельно, поскольку их можно в высокой степени оптимизировать.

Некоторые версии используют принципы Брезенхэма о целочисленной инкрементной ошибке для выполнения всех октантных линий, уравновешивая положительную и отрицательную ошибку между координатами x и y. ^[3]

plotLine(x0, y0, x1, y1) dx = абс(x1 - x0) sx = x0 < x1 ? 1 : -1 dy = -abs(y1 - y0) sy = y0 < y1 ? 1 : -1 ошибка = dx + dy  в то время как правда график(x0, y0) если x0 == x1 && y0 == y1 перерыв е2 = 2 * ошибка если е2 >= dy ошибка = ошибка + dy х0 = х0 + сх конец если  если e2 <= dx ошибка = ошибка + dx у0 = у0 + си конец если  конец пока

Похожие алгоритмы

Алгоритм Брезенхэма можно интерпретировать как слегка модифицированный цифровой дифференциальный анализатор (использующий 0,5 в качестве порога ошибки вместо 0, который требуется для растеризации неперекрывающихся полигонов).

Принцип использования инкрементной ошибки вместо операций деления имеет и другие приложения в графике. Можно использовать эту технику для вычисления координат U, V во время растрового сканирования текстурированных полигонов. ^[4] Программные движки рендеринга воксельных высот, которые можно увидеть в некоторых играх для ПК, также использовали этот принцип.

Брезенхэм также опубликовал вычислительный алгоритм Run-Slice: в то время как описанный выше алгоритм Run-Length запускает цикл по большой оси, вариация Run-Slice запускает цикл в другую сторону. ^[5] Этот метод был представлен в ряде патентов США:

Алгоритм был расширен до:

• Рисуйте линии произвольной толщины, алгоритм, созданный Аланом Мерфи в IBM. ^[6]
• Рисование кривых различных видов (кругов, эллипсов, кубических, квадратичных и рациональных кривых Безье), а также сглаженных линий и кривых; набор алгоритмов Алоиса Цингля. ^[3]

Смотрите также

• Цифровой дифференциальный анализатор (графический алгоритм) , простой и общий метод растеризации линий и треугольников.
• Алгоритм линий Сяолиня У , аналогичный быстрый метод рисования линий со сглаживанием
• Алгоритм построения окружности посередине , аналогичный алгоритм для рисования окружностей

Примечания

1. Пол Э. Блэк. Словарь алгоритмов и структур данных, NIST . https://xlinux.nist.gov/dads/HTML/bresenham.html
2. Джой, Кеннет. «Алгоритм Брезенхэма» (PDF) . Исследовательская группа визуализации и графики, кафедра компьютерных наук, Калифорнийский университет в Дэвисе . Получено 20 декабря 2016 г. .
3. Zingl, Alois (2012). Алгоритм растеризации для рисования кривых (PDF) (Отчет).
   Аннотация и демонстрация HTML: Зингл, Алоис (2016). «Бресенхем». Members.chello.at .
4. US 5739818, Spackman, John Neil, «Устройство и метод выполнения перспективно корректной интерполяции в компьютерной графике», опубликовано 14.04.1998, передано Canon KK 
5. "Michael Abrash's Graphics Programming Black Book Special Edition: The Good, the Bad, and the Run-Sliced". www.phatcode.net . Получено 13 февраля 2024 г.;
6. "Модифицированный алгоритм Брезенхэма линии Мерфи". homepages.enterprise.net . Получено 2018-06-09 .(«Утолщение линий путем модификации алгоритма Брезенхэма» в Техническом бюллетене IBM, том 20, № 12, май 1978 г., страницы 5358–5366.)

Ссылки

• Брезенхэм, Дж. Э. (1965). «Алгоритм для компьютерного управления цифровым плоттером» (PDF) . IBM Systems Journal . 4 (1): 25–30. doi :10.1147/sj.41.0025. Архивировано из оригинала (PDF) 28 мая 2008 г.
• «Алгоритм рисования линий Брезенхэма», Колин Фланаган
• Абраш, Майкл (1997). Черная книга по графическому программированию Майкла Абраша . Олбани, Нью-Йорк: Coriolis. С. 654–678. ISBN 978-1-57610-174-2.Очень оптимизированная версия алгоритма на языке C и ассемблере для использования в видеоиграх с полным описанием его внутренней работы.
• Цингль, Алоис (2012). «Растеризующий алгоритм для рисования кривых» (PDF) ., Красота алгоритмов Брезенхэма

Дальнейшее чтение

• Диссертация Патрика-Гиллесбанда, содержащая расширение алгоритма рисования линий Брезенхэма для удаления скрытых трехмерных линий.
  • также опубликовано в трудах MICAD '87 по CAD/CAM и компьютерной графике, стр. 591 - ISBN 2-86601-084-1 . 
• Утолщение линий путем модификации алгоритма Брезенхэма, AS Murphy, IBM Technical Disclosure Bulletin, том 20, № 12, май 1978 г.
• Брезенхэм, Джек (февраль 1977 г.). «Линейный алгоритм для инкрементального цифрового отображения дуг окружностей». Сообщения ACM . 20 (2): 100–106. doi :10.1145/359423.359432.– также Технический отчет 1964 Янв-27 -11- Алгоритм круга TR-02-286 IBM San Jose Lab

Внешние ссылки

• Специальное издание книги Майкла Абраша «Graphics Programming Black Book»: Глава 35: Брезенхэм — это быстро, а быстро — это хорошо
• Алгоритм рисования линий Брезенхэма Колина Фланагана
• Страница Национального института стандартов и технологий об алгоритме Брезенхэма
• Информация о инкрементальном плоттере Calcomp 563
• Алгоритм Брезенхэма в нескольких языках программирования
• Красота алгоритма Брезенхэма – простая реализация для построения линий, окружностей, эллипсов и кривых Безье