Алгоритм двоичного поиска

Search algorithm finding the position of a target value within a sorted array

В информатике двоичный поиск , также известный как полуинтервальный поиск , ^[1] логарифмический поиск , ^[2] или бинарный поиск , ^[3] — это алгоритм поиска , который находит положение целевого значения в отсортированном массиве . ^{[4] [5]} Бинарный поиск сравнивает целевое значение со средним элементом массива. Если они не равны, половина, в которой цель не может находиться, удаляется, и поиск продолжается на оставшейся половине, снова беря средний элемент для сравнения с целевым значением и повторяя это до тех пор, пока целевое значение не будет найдено. Если поиск заканчивается, а оставшаяся половина пуста, цель отсутствует в массиве.

Бинарный поиск в худшем случае выполняется за логарифмическое время , производя сравнения, где – количество элементов в массиве. ^{[a] [6]} Бинарный поиск быстрее линейного поиска , за исключением небольших массивов. Однако сначала массив необходимо отсортировать, чтобы можно было применить двоичный поиск. Существуют специализированные структуры данных , предназначенные для быстрого поиска, такие как хэш-таблицы , поиск по которым можно осуществлять более эффективно, чем двоичный поиск. Однако двоичный поиск можно использовать для решения более широкого круга задач, например, для поиска следующего по наименьшему или по величине элемента в массиве относительно целевого объекта, даже если он отсутствует в массиве. ${\displaystyle O(\log n)}$ ${\displaystyle n}$

Существует множество вариантов двоичного поиска. В частности, дробное каскадирование ускоряет двоичный поиск одного и того же значения в нескольких массивах. Дробное каскадирование эффективно решает ряд поисковых задач в вычислительной геометрии и во многих других областях. Экспоненциальный поиск расширяет двоичный поиск до неограниченных списков. Дерево двоичного поиска и структуры данных B-дерева основаны на двоичном поиске.

Алгоритм

Бинарный поиск работает с отсортированными массивами. Бинарный поиск начинается со сравнения элемента в середине массива с целевым значением. Если целевое значение соответствует элементу, возвращается его позиция в массиве. Если целевое значение меньше элемента, поиск продолжается в нижней половине массива. Если целевое значение больше элемента, поиск продолжается в верхней половине массива. При этом алгоритм на каждой итерации исключает половину, в которой целевое значение не может находиться. ^[7]

Процедура

Учитывая массив элементов со значениями или записями , отсортированными таким образом , что и целевое значение , следующая подпрограмма использует двоичный поиск, чтобы найти индекс in . ^[7] ${\displaystyle A}$ ${\displaystyle n}$ ${\displaystyle A_{0},A_{1},A_{2},\ldots ,A_{n-1}}$ ${\displaystyle A_{0}\leq A_{1}\leq A_{2}\leq \cdots \leq A_{n-1}}$ ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle A}$

1. Установите на и на . ${\displaystyle L}$ ${\displaystyle 0}$ ${\displaystyle R}$ ${\displaystyle n-1}$
2. Если , поиск завершается как безуспешный. ${\displaystyle L>R}$
3. Установите (положение среднего элемента) на нижний уровень , который является наибольшим целым числом, меньшим или равным . ${\displaystyle m}$ ${\displaystyle {\frac {L+R}{2}}}$ ${\displaystyle {\frac {L+R}{2}}}$
4. Если , установите значение и перейдите к шагу 2. ${\displaystyle A_{m}<T}$ ${\displaystyle L}$ ${\displaystyle m+1}$
5. Если , установите значение и перейдите к шагу 2. ${\displaystyle A_{m}>T}$ ${\displaystyle R}$ ${\displaystyle m-1}$
6. Теперь поиск завершен; возвращаться . ${\displaystyle A_{m}=T}$ ${\displaystyle m}$

Эта итерационная процедура отслеживает границы поиска с помощью двух переменных и . Процедура может быть выражена в псевдокоде следующим образом, где имена и типы переменных остаются такими же, как указано выше, это функция пола и ссылается на конкретное значение, которое сообщает о неудаче поиска. ^[7] ${\displaystyle L}$ ${\displaystyle R}$floorunsuccessful

двоичный поиск

функцияbinary_search (A, n, T ) Л := 0 р := п - 1 в то время как L ≤ R делать м := пол((L + R) / 2) если A[m] < T , то Л := м + 1 иначе, если A[m] > T , то р := м - 1 else : возврат m возврат неуспешный

В качестве альтернативы алгоритм может принять потолок . Это может изменить результат, если целевое значение появляется в массиве более одного раза. ${\displaystyle {\frac {L+R}{2}}}$

Альтернативная процедура

В приведенной выше процедуре алгоритм проверяет, равен ли средний элемент ( ) целевому элементу ( ) на каждой итерации. Некоторые реализации исключают эту проверку во время каждой итерации. Алгоритм будет выполнять эту проверку только тогда, когда останется один элемент (когда ). Это приводит к более быстрому циклу сравнения, поскольку на каждой итерации исключается одно сравнение, хотя в среднем требуется только одна дополнительная итерация. ^[8] ${\displaystyle m}$ ${\displaystyle T}$ ${\displaystyle L=R}$

Герман Боттенбрух опубликовал первую реализацию, в которой эта проверка не учитывалась, в 1962 году. ^{[8] [9]}

1. Установите на и на . ${\displaystyle L}$ ${\displaystyle 0}$ ${\displaystyle R}$ ${\displaystyle n-1}$
2. Пока , ${\displaystyle L\neq R}$
   1. Установите (положение среднего элемента) на потолок , который является наименьшим целым числом, большим или равным . ${\displaystyle m}$ ${\displaystyle {\frac {L+R}{2}}}$ ${\displaystyle {\frac {L+R}{2}}}$
   2. Если , установите . ${\displaystyle A_{m}>T}$ ${\displaystyle R}$ ${\displaystyle m-1}$
   3. Еще, ; установлен в . ${\displaystyle A_{m}\leq T}$ ${\displaystyle L}$ ${\displaystyle m}$
3. Итак , поиск завершен. Если , вернитесь . В противном случае поиск завершается как безуспешный. ${\displaystyle L=R}$ ${\displaystyle A_{L}=T}$ ${\displaystyle L}$

Где ceilнаходится функция потолка, псевдокод для этой версии:

функцияbinary_search_alternative (A, n, T ) Л := 0 р := п - 1 в то время как L != R делать м := ячейка((L + R)/2) если A[m] > T , то р := м - 1 еще : Л := м если A[L] = T , то  вернуть L возврат неудачный

Дублирующиеся элементы

Процедура может вернуть любой индекс, элемент которого равен целевому значению, даже если в массиве есть повторяющиеся элементы. Например, если массив, в котором нужно выполнить поиск, был и цель была , то для алгоритма было бы правильно возвращать либо 4-й (индекс 3), либо 5-й (индекс 4) элемент. В этом случае обычная процедура вернет четвертый элемент (индекс 3). Он не всегда возвращает первый дубликат (учтите , который по-прежнему возвращает 4-й элемент). Однако иногда необходимо найти самый левый или самый правый элемент для целевого значения, которое дублируется в массиве. В приведенном выше примере 4-й элемент — это самый левый элемент значения 4, а 5-й элемент — это самый правый элемент значения 4. Альтернативная процедура, описанная выше, всегда будет возвращать индекс самого правого элемента, если такой элемент существует. ^[9] ${\displaystyle [1,2,3,4,4,5,6,7]}$ ${\displaystyle 4}$ ${\displaystyle [1,2,4,4,4,5,6,7]}$

Процедура поиска крайнего левого элемента

Чтобы найти самый левый элемент, можно использовать следующую процедуру: ^[10]

1. Установите на и на . ${\displaystyle L}$ ${\displaystyle 0}$ ${\displaystyle R}$ ${\displaystyle n}$
2. Пока , ${\displaystyle L<R}$
   1. Установите (положение среднего элемента) на нижний уровень , который является наибольшим целым числом, меньшим или равным . ${\displaystyle m}$ ${\displaystyle {\frac {L+R}{2}}}$ ${\displaystyle {\frac {L+R}{2}}}$
   2. Если , установите . ${\displaystyle A_{m}<T}$ ${\displaystyle L}$ ${\displaystyle m+1}$
   3. Еще, ; установлен в . ${\displaystyle A_{m}\geq T}$ ${\displaystyle R}$ ${\displaystyle m}$
3. Возвращаться . ${\displaystyle L}$

Если и , то это самый левый элемент, равный . Даже если его нет в массиве, это ранг в массиве или количество элементов в массиве, меньших . ${\displaystyle L<n}$ ${\displaystyle A_{L}=T}$ ${\displaystyle A_{L}}$ ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle L}$ ${\displaystyle T}$ ${\displaystyle T}$

Где floorнаходится функция пола, псевдокод для этой версии:

функцияbinary_search_leftmost (A, n, T): Л := 0 Р := п в то время как L < R: м := пол((L + R) / 2) если А[м] < Т: Л := м + 1 еще : Р := м вернуть Л

Процедура поиска самого правого элемента

Чтобы найти самый правый элемент, можно использовать следующую процедуру: ^[10]

1. Установите на и на . ${\displaystyle L}$ ${\displaystyle 0}$ ${\displaystyle R}$ ${\displaystyle n}$
2. Пока , ${\displaystyle L<R}$
   1. Установите (положение среднего элемента) на нижний уровень , который является наибольшим целым числом, меньшим или равным . ${\displaystyle m}$ ${\displaystyle {\frac {L+R}{2}}}$ ${\displaystyle {\frac {L+R}{2}}}$
   2. Если , установите . ${\displaystyle A_{m}>T}$ ${\displaystyle R}$ ${\displaystyle m}$
   3. Еще, ; установлен в . ${\displaystyle A_{m}\leq T}$ ${\displaystyle L}$ ${\displaystyle m+1}$
3. Возвращаться . ${\displaystyle R-1}$

Если и , то это самый правый элемент, равный . Даже если его нет в массиве, это количество элементов в массиве, превышающее . ${\displaystyle R>0}$ ${\displaystyle A_{R-1}=T}$ ${\displaystyle A_{R-1}}$ ${\displaystyle T}$ ${\displaystyle T}$ ${\displaystyle n-R}$ ${\displaystyle T}$

Где floorнаходится функция пола, псевдокод для этой версии:

функцияbinary_search_rightmost (A, n, T): Л := 0 Р := п в то время как L < R: м := пол((L + R) / 2) если А[м] > Т: Р := м еще : Л := м + 1 вернуть Р - 1

Приблизительные совпадения

Бинарный поиск можно адаптировать для вычисления приблизительных совпадений. В приведенном выше примере для целевого значения , которого нет в массиве, показаны ранг, предшественник, преемник и ближайший сосед . ${\displaystyle 5}$

Вышеуказанная процедура выполняет только точные совпадения, находя положение целевого значения. Однако расширить двоичный поиск для выполнения приблизительных совпадений тривиально, поскольку двоичный поиск работает с отсортированными массивами. Например, двоичный поиск можно использовать для вычисления для данного значения его ранга (количества меньших элементов), предшественника (следующего наименьшего элемента), преемника (следующего по величине элемента) и ближайшего соседа . Запросы диапазона , определяющие количество элементов между двумя значениями, могут выполняться с помощью двух ранговых запросов. ^[11]

• Запросы ранга могут выполняться с помощью процедуры поиска крайнего левого элемента. Процедура возвращает количество элементов меньше целевого значения. ^[11]
• Запросы-предшественники могут выполняться с помощью ранговых запросов. Если ранг целевого значения равен , его предшественник равен  . ^[12] ${\displaystyle r}$ ${\displaystyle r-1}$
• Для запросов-преемников можно использовать процедуру поиска самого правого элемента. Если результатом выполнения процедуры для целевого значения является , то преемником целевого значения является  . ^[12] ${\displaystyle r}$ ${\displaystyle r+1}$
• Ближайшим соседом целевого значения является либо его предшественник, либо преемник, в зависимости от того, что ближе.
• Запросы диапазона также просты. ^[12] Как только ранги двух значений известны, количество элементов, больше или равное первому значению и меньше второго, является разницей двух рангов. Это количество можно увеличить или уменьшить на единицу в зависимости от того, следует ли считать конечные точки диапазона частью диапазона и содержит ли массив записи, соответствующие этим конечным точкам. ^[13]

Производительность

Дерево , представляющее двоичный поиск. Здесь ищется массив , а целевое значение – . ${\displaystyle [20,30,40,50,80,90,100]}$ ${\displaystyle 40}$

Наихудший случай достигается, когда поиск достигает самого глубокого уровня дерева, а лучший случай достигается, когда целевым значением является средний элемент.

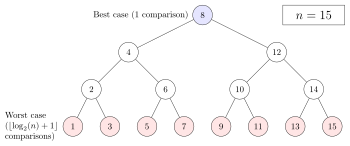
Что касается количества сравнений, производительность бинарного поиска можно проанализировать, просматривая выполнение процедуры в бинарном дереве. Корневой узел дерева является средним элементом массива. Средний элемент нижней половины — это левый дочерний узел корня, а средний элемент верхней половины — правый дочерний узел корня. Остальная часть дерева строится аналогичным образом. Начиная с корневого узла, просматриваются левые или правые поддеревья в зависимости от того, меньше или больше целевое значение рассматриваемого узла. ^{[6] [14]}

В худшем случае двоичный поиск выполняет итерации цикла сравнения, где обозначение обозначает нижнюю функцию , которая возвращает наибольшее целое число, меньшее или равное аргументу, и представляет собой двоичный логарифм . Это связано с тем, что худший случай достигается, когда поиск достигает самого глубокого уровня дерева, а в дереве всегда есть уровни для любого двоичного поиска. ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ ${\textstyle \lfloor \cdot \rfloor }$ ${\textstyle \log _{2}}$ ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$

Худший случай также может возникнуть, когда целевой элемент отсутствует в массиве. Если на единицу меньше степени двойки, то это всегда так. В противном случае поиск может выполнять итерации, если поиск достигает самого глубокого уровня дерева. Однако он может делать итерации, что на одну меньше, чем в худшем случае, если поиск заканчивается на втором по глубине уровне дерева. ^[15] ${\textstyle n}$ ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ ${\textstyle \lfloor \log _{2}(n)\rfloor }$

В среднем, если предположить, что каждый элемент будет найден с одинаковой вероятностью, двоичный поиск выполняет итерации, когда целевой элемент находится в массиве. Это примерно равно итерациям. Когда целевой элемент отсутствует в массиве, двоичный поиск в среднем выполняет итерации, предполагая, что диапазон между элементами и внешними элементами будет найден с одинаковой вероятностью. ^[14] ${\displaystyle \lfloor \log _{2}(n)\rfloor +1-(2^{\lfloor \log _{2}(n)\rfloor +1}-\lfloor \log _{2}(n)\rfloor -2)/n}$ ${\displaystyle \log _{2}(n)-1}$ ${\displaystyle \lfloor \log _{2}(n)\rfloor +2-2^{\lfloor \log _{2}(n)\rfloor +1}/(n+1)}$

В лучшем случае, когда целевым значением является средний элемент массива, его позиция возвращается после одной итерации. ^[16]

С точки зрения итераций ни один алгоритм поиска, работающий только путем сравнения элементов, не может показать лучшую производительность в среднем и худшем случае, чем двоичный поиск. Дерево сравнения, представляющее бинарный поиск, имеет минимально возможное количество уровней, поскольку каждый уровень выше самого нижнего уровня дерева заполняется полностью. ^[b] В противном случае алгоритм поиска может исключить несколько элементов за итерацию, увеличивая количество итераций, необходимых в среднем и худшем случае. Это относится и к другим алгоритмам поиска, основанным на сравнениях, поскольку, хотя они могут работать быстрее с некоторыми целевыми значениями, средняя производительность по всем элементам хуже, чем у двоичного поиска. Разделив массив пополам, двоичный поиск гарантирует, что размеры обоих подмассивов будут максимально похожими. ^[14]

Пространственная сложность

Двоичный поиск требует трех указателей на элементы, которые могут быть индексами массива или указателями на ячейки памяти, независимо от размера массива. Следовательно, пространственная сложность двоичного поиска заключается в модели вычислений в словесной оперативной памяти . ${\displaystyle O(1)}$

Вывод среднего случая

Среднее количество итераций, выполняемых бинарным поиском, зависит от вероятности каждого искомого элемента. В среднем случай успешных и неудачных поисков различается. Предполагается, что каждый элемент с равной вероятностью будет найден для успешного поиска. В случае неудачных поисков предполагается, что интервалы между элементами и за их пределами будут обысканы с одинаковой вероятностью. Средний случай успешного поиска — это количество итераций, необходимых для поиска каждого элемента ровно один раз, разделенное на количество элементов. Средний случай неудачных поисков — это количество итераций, необходимых для поиска элемента в каждом интервале ровно один раз, разделенное на интервалы . ^[14] ${\displaystyle n}$ ${\displaystyle n+1}$

Успешные поиски

В представлении двоичного дерева успешный поиск может быть представлен путем от корня до целевого узла, называемым внутренним путем . Длина пути — это количество ребер (соединений между узлами), через которые проходит путь. Количество итераций, выполненных при поиске, учитывая, что соответствующий путь имеет длину , считается начальной итерацией. Длина внутреннего пути — это сумма длин всех уникальных внутренних путей. Поскольку существует только один путь от корня до любого отдельного узла, каждый внутренний путь представляет собой поиск определенного элемента. Если есть элементы, которые являются положительным целым числом, а длина внутреннего пути равна , то среднее количество итераций для успешного поиска с добавлением одной итерации для подсчета начальной итерации. ^[14] ${\displaystyle l}$ ${\displaystyle l+1}$ ${\displaystyle n}$ ${\displaystyle I(n)}$ ${\displaystyle T(n)=1+{\frac {I(n)}{n}}}$

Поскольку бинарный поиск является оптимальным алгоритмом поиска со сравнениями, данная задача сводится к вычислению минимальной длины внутреннего пути всех бинарных деревьев с узлами, которая равна: ^[17] ${\displaystyle n}$

${\displaystyle I(n)=\sum _{k=1}^{n}\left\lfloor \log _{2}(k)\right\rfloor }$

Например, в массиве из 7 элементов корень требует одной итерации, два элемента ниже корня требуют двух итераций, а четыре элемента ниже требуют трех итераций. В этом случае длина внутреннего пути равна: ^[17]

${\displaystyle \sum _{k=1}^{7}\left\lfloor \log _{2}(k)\right\rfloor =0+2(1)+4(2)=2+8=10}$

Среднее количество итераций будет основано на уравнении для среднего случая. Сумма для может быть упрощена до: ^[14] ${\displaystyle 1+{\frac {10}{7}}=2{\frac {3}{7}}}$ ${\displaystyle I(n)}$

${\displaystyle I(n)=\sum _{k=1}^{n}\left\lfloor \log _{2}(k)\right\rfloor =(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2}$

Подставив уравнение для в уравнение для : ^[14] ${\displaystyle I(n)}$ ${\displaystyle T(n)}$

${\displaystyle T(n)=1+{\frac {(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2}{n}}=\lfloor \log _{2}(n)\rfloor +1-(2^{\lfloor \log _{2}(n)\rfloor +1}-\lfloor \log _{2}(n)\rfloor -2)/n}$

Для целого числа это эквивалентно уравнению для среднего случая успешного поиска, указанному выше. ${\displaystyle n}$

Неудачные поиски

Неудачные поиски можно представить путем дополнения дерева внешними узлами , что образует расширенное двоичное дерево . Если внутренний узел или узел, присутствующий в дереве, имеет менее двух дочерних узлов, то добавляются дополнительные дочерние узлы, называемые внешними узлами, так что у каждого внутреннего узла есть два дочерних узла. Таким образом, неудачный поиск можно представить как путь к внешнему узлу, родителем которого является единственный элемент, оставшийся во время последней итерации. Внешний путь — это путь от корня к внешнему узлу. Длина внешнего пути представляет собой сумму длин всех уникальных внешних путей. Если есть элементы, которые являются положительным целым числом, а длина внешнего пути равна , то среднее количество итераций для неудачного поиска с добавлением одной итерации для подсчета начальной итерации. Длина внешнего пути делится на вместо, потому что существуют внешние пути, представляющие интервалы между элементами массива и за их пределами. ^[14] ${\displaystyle n}$ ${\displaystyle E(n)}$ ${\displaystyle T'(n)={\frac {E(n)}{n+1}}}$ ${\displaystyle n+1}$ ${\displaystyle n}$ ${\displaystyle n+1}$

Эту задачу аналогичным образом можно свести к определению минимальной длины внешнего пути всех бинарных деревьев с узлами. Для всех двоичных деревьев длина внешнего пути равна длине внутреннего пути плюс . ^[17] Подставляя уравнение для : ^[14] ${\displaystyle n}$ ${\displaystyle 2n}$ ${\displaystyle I(n)}$

${\displaystyle E(n)=I(n)+2n=\left[(n+1)\left\lfloor \log _{2}(n+1)\right\rfloor -2^{\left\lfloor \log _{2}(n+1)\right\rfloor +1}+2\right]+2n=(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}}$

Подставив уравнение для в уравнение для можно определить средний случай неудачных поисков: ^[14] ${\displaystyle E(n)}$ ${\displaystyle T'(n)}$

${\displaystyle T'(n)={\frac {(n+1)(\lfloor \log _{2}(n)\rfloor +2)-2^{\lfloor \log _{2}(n)\rfloor +1}}{(n+1)}}=\lfloor \log _{2}(n)\rfloor +2-2^{\lfloor \log _{2}(n)\rfloor +1}/(n+1)}$

Проведение альтернативной процедуры

Каждая итерация процедуры двоичного поиска, определенной выше, выполняет одно или два сравнения, проверяя, равен ли средний элемент целевому элементу на каждой итерации. Предполагая, что каждый элемент будет найден с одинаковой вероятностью, каждая итерация выполняет в среднем 1,5 сравнения. Вариант алгоритма проверяет, равен ли средний элемент целевому элементу в конце поиска. В среднем это исключает половину сравнения на каждой итерации. Это немного сокращает время, затрачиваемое на итерацию на большинстве компьютеров. Однако он гарантирует, что поиск займет максимальное количество итераций, добавляя в среднем одну итерацию к поиску. Поскольку в худшем случае цикл сравнения выполняется только один раз, небольшое увеличение эффективности на итерацию не компенсирует дополнительную итерацию для всех, кроме очень больших . ^{[с] [18] [19]} ${\textstyle \lfloor \log _{2}(n)+1\rfloor }$ ${\textstyle n}$

Время работы и использование кэша

При анализе производительности бинарного поиска еще одним фактором является время, необходимое для сравнения двух элементов. Для целых чисел и строк требуемое время увеличивается линейно по мере увеличения длины кодирования (обычно количества битов ) элементов. Например, сравнение пары 64-битных целых чисел без знака потребует сравнения вдвое большего количества битов, чем сравнение пары 32-битных целых чисел без знака. Худший случай достигается, когда целые числа равны. Это может быть важно, когда длина кодирования элементов велика, например, при больших целочисленных типах или длинных строках, что делает сравнение элементов дорогостоящим. Более того, сравнение значений с плавающей запятой (наиболее распространенное цифровое представление действительных чисел ) часто обходится дороже, чем сравнение целых чисел или коротких строк.

В большинстве компьютерных архитектур процессор имеет аппаратный кэш , отдельный от оперативной памяти . Поскольку они расположены внутри самого процессора, доступ к кэшам осуществляется гораздо быстрее, но обычно они хранят гораздо меньше данных, чем оперативная память. Таким образом, большинство процессоров хранят ячейки памяти, к которым недавно осуществлялся доступ, а также ячейки памяти, близкие к ним. Например, при доступе к элементу массива сам элемент может быть сохранен вместе с элементами, которые хранятся рядом с ним в оперативной памяти, что ускоряет последовательный доступ к элементам массива, которые близки по индексу друг к другу ( локальность ссылки ). . В отсортированном массиве двоичный поиск может переходить к удаленным областям памяти, если массив большой, в отличие от алгоритмов (таких как линейный поиск и линейное зондирование в хеш-таблицах ), которые обращаются к элементам последовательно. Это немного увеличивает время выполнения двоичного поиска больших массивов в большинстве систем. ^[20]

Бинарный поиск по сравнению с другими схемами

Сортированные массивы с двоичным поиском являются очень неэффективным решением, когда операции вставки и удаления чередуются с поиском, и на каждую такую ​​операцию уходит время. Кроме того, отсортированные массивы могут усложнить использование памяти, особенно если в массив часто вставляются элементы. ^[21] Существуют и другие структуры данных, которые поддерживают гораздо более эффективную вставку и удаление. Бинарный поиск можно использовать для выполнения точного сопоставления и установки членства (определения того, находится ли целевое значение в коллекции значений). Существуют структуры данных, которые поддерживают более быстрое точное сопоставление и набор членства. Однако, в отличие от многих других схем поиска, двоичный поиск можно использовать для эффективного приблизительного сопоставления, обычно выполняя такие сопоставления во времени независимо от типа или структуры самих значений. ^[22] Кроме того, есть некоторые операции, такие как поиск наименьшего и самого большого элемента, которые можно эффективно выполнять с отсортированным массивом. ^[11] ${\textstyle O(n)}$ ${\textstyle O(\log n)}$

Линейный поиск

Линейный поиск — это простой алгоритм поиска, который проверяет каждую запись, пока не найдет целевое значение. Линейный поиск может выполняться в связанном списке, что позволяет выполнять вставку и удаление быстрее, чем в массиве. Бинарный поиск в отсортированных массивах выполняется быстрее, чем линейный поиск, за исключением случаев, когда массив короткий, хотя массив необходимо отсортировать заранее. ^{[d] [24]} Все алгоритмы сортировки , основанные на сравнении элементов, такие как быстрая сортировка и сортировка слиянием , требуют как минимум сравнения в худшем случае. ^[25] В отличие от линейного поиска, двоичный поиск может использоваться для эффективного приблизительного сопоставления. Существуют такие операции, как поиск наименьшего и самого большого элемента, которые можно эффективно выполнить в отсортированном массиве, но не в несортированном. ^[26] ${\textstyle O(n\log n)}$

Деревья

Деревья двоичного поиска ищутся с использованием алгоритма, аналогичного двоичному поиску.

Дерево двоичного поиска — это структура данных двоичного дерева , работающая по принципу двоичного поиска. Записи дерева расположены в отсортированном порядке, и каждая запись в дереве может быть найдена с использованием алгоритма, аналогичного бинарному поиску, занимающего среднее логарифмическое время. Вставка и удаление также требуют в среднем логарифмического времени в двоичных деревьях поиска. Это может быть быстрее, чем вставка и удаление отсортированных массивов с линейным временем, а двоичные деревья сохраняют способность выполнять все возможные операции с отсортированным массивом, включая диапазон и приблизительные запросы. ^{[22] [27]}

Однако двоичный поиск обычно более эффективен для поиска, поскольку деревья двоичного поиска, скорее всего, будут несовершенно сбалансированы, что приводит к несколько худшей производительности, чем двоичный поиск. Это относится даже к сбалансированным двоичным деревьям поиска , двоичным деревьям поиска, которые балансируют свои собственные узлы, поскольку они редко создают дерево с наименьшим возможным количеством уровней. За исключением сбалансированных двоичных деревьев поиска, дерево может быть сильно несбалансированным с небольшим количеством внутренних узлов с двумя дочерними узлами, в результате чего среднее и наихудшее время поиска приближается к сравнению. ^[e] Двоичные деревья поиска занимают больше места, чем отсортированные массивы. ^[29] ${\textstyle n}$

Деревья двоичного поиска пригодны для быстрого поиска во внешней памяти, хранящейся на жестких дисках, поскольку деревья двоичного поиска могут быть эффективно структурированы в файловых системах. B -дерево обобщает этот метод организации дерева. B-деревья часто используются для организации долговременного хранилища, например баз данных и файловых систем . ^{[30] [31]}

Хеширование

Для реализации ассоциативных массивов хэш - таблицы — структура данных, которая сопоставляет ключи с записями с помощью хэш-функции — обычно быстрее, чем двоичный поиск в отсортированном массиве записей. ^[32] Для большинства реализаций хеш-таблиц в среднем требуется только амортизированное постоянное время. ^{[f] [34]} Однако хеширование бесполезно для приблизительных совпадений, таких как вычисление следующего наименьшего, следующего по величине и ближайшего ключа, поскольку единственная информация, предоставляемая в случае неудачного поиска, заключается в том, что цель отсутствует ни в одном записывать. ^[35] Двоичный поиск идеально подходит для таких совпадений, выполняя их за логарифмическое время. Бинарный поиск также поддерживает приблизительные совпадения. Некоторые операции, например поиск наименьшего и наибольшего элемента, можно эффективно выполнять с отсортированными массивами, но не с хеш-таблицами. ^[22]

Установите алгоритмы членства

Проблема, связанная с поиском, — это членство в наборе . Любой алгоритм, выполняющий поиск, например двоичный поиск, также может использоваться для определения членства во множестве. Существуют и другие алгоритмы, которые более подходят для определения членства во множестве. Битовый массив является самым простым и полезен, когда диапазон ключей ограничен. Он компактно хранит набор битов , каждый бит представляет один ключ в диапазоне ключей. Битовые массивы работают очень быстро, требуя только времени. ^[36] Массив Judy типа Judy1 эффективно обрабатывает 64-битные ключи. ^[37] ${\textstyle O(1)}$

Для получения приблизительных результатов фильтры Блума , еще одна вероятностная структура данных, основанная на хешировании, хранят набор ключей путем кодирования ключей с использованием битового массива и нескольких хеш-функций. Фильтры Блума в большинстве случаев гораздо более эффективны, чем битовые массивы, и не намного медленнее: с помощью хэш-функций запросы на членство требуют только времени. Однако фильтры Блума страдают от ложных срабатываний . ^{[г] [ч] [39]} ${\textstyle k}$ ${\textstyle O(k)}$

Другие структуры данных

Существуют структуры данных, которые в некоторых случаях могут улучшить двоичный поиск как для поиска, так и для других операций, доступных для отсортированных массивов. Например, поиск, приблизительные совпадения и операции, доступные для отсортированных массивов, могут выполняться более эффективно, чем двоичный поиск, в специализированных структурах данных, таких как деревья Ван Эмде Боаса , деревья слияния , попытки и битовые массивы . Эти специализированные структуры данных обычно работают быстрее только потому, что они используют свойства ключей с определенным атрибутом (обычно ключей, которые являются небольшими целыми числами), и, следовательно, для ключей, у которых нет этого атрибута, потребуется много времени или места. ^[22] Пока ключи можно упорядочить, эти операции всегда можно выполнить как минимум эффективно с отсортированным массивом независимо от ключей. Некоторые структуры, такие как массивы Джуди, используют комбинацию подходов, чтобы смягчить это, сохраняя при этом эффективность и способность выполнять приблизительное сопоставление. ^[37]

Вариации

Единый двоичный поиск

Равномерный двоичный поиск сохраняет разницу между текущим и двумя следующими возможными средними элементами вместо конкретных границ.

Равномерный двоичный поиск вместо нижней и верхней границ хранит разницу в индексе среднего элемента от текущей итерации до следующей итерации. Таблица поиска , содержащая различия, вычисляется заранее. Например, если массив, в котором нужно выполнить поиск, — [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11] , средний элемент ( ) будет 6 . В этом случае средний элемент левого подмассива ( [1, 2, 3, 4, 5] ) равен 3 , а средний элемент правого подмассива ( [7, 8, 9, 10, 11] ) равен 9 . Равномерный двоичный поиск будет хранить значение 3 , поскольку оба индекса отличаются от 6 на одну и ту же величину. ^[40] Чтобы уменьшить пространство поиска, алгоритм либо добавляет, либо вычитает это изменение из индекса среднего элемента. Равномерный двоичный поиск может быть быстрее в системах, где вычисление средней точки неэффективно, например, на компьютерах с десятичной дробью . ^[41] ${\displaystyle m}$

Экспоненциальный поиск

Визуализация экспоненциального поиска с поиском верхней границы для последующего бинарного поиска

Экспоненциальный поиск расширяет двоичный поиск до неограниченных списков. Он начинается с поиска первого элемента с индексом, который равен степени двойки и превышает целевое значение. После этого он устанавливает этот индекс в качестве верхней границы и переключается на двоичный поиск. Поиск занимает несколько итераций до запуска двоичного поиска и максимум итераций двоичного поиска, где находится позиция целевого значения. Экспоненциальный поиск работает с ограниченными списками, но становится улучшением по сравнению с бинарным поиском, только если целевое значение находится недалеко от начала массива. ^[42] ${\textstyle \lfloor \log _{2}x+1\rfloor }$ ${\textstyle \lfloor \log _{2}x\rfloor }$ ${\textstyle x}$

Интерполяционный поиск

Визуализация интерполяционного поиска с использованием линейной интерполяции. В этом случае поиск не требуется, поскольку оценка местоположения цели в массиве верна. Другие реализации могут указывать другую функцию для оценки местоположения цели.

Вместо вычисления средней точки интерполяционный поиск оценивает положение целевого значения, принимая во внимание самый низкий и самый высокий элементы в массиве, а также длину массива. Это работает на том основании, что во многих случаях средняя точка не является лучшим предположением. Например, если целевое значение близко к самому высокому элементу массива, оно, скорее всего, будет расположено ближе к концу массива. ^[43]

Распространенной функцией интерполяции является линейная интерполяция . Если — массив, — нижняя и верхняя границы соответственно, и — цель, то, по оценкам, цель находится примерно на расстоянии между и . Когда используется линейная интерполяция и распределение элементов массива равномерное или близкое к равномерному, интерполяционный поиск выполняет сравнения. ^{[43] [44] [45]} ${\displaystyle A}$ ${\displaystyle L,R}$ ${\displaystyle T}$ ${\displaystyle (T-A_{L})/(A_{R}-A_{L})}$ ${\displaystyle L}$ ${\displaystyle R}$ ${\textstyle O(\log \log n)}$

На практике интерполяционный поиск медленнее, чем двоичный поиск для небольших массивов, поскольку интерполяционный поиск требует дополнительных вычислений. Его временная сложность растет медленнее, чем двоичный поиск, но это компенсирует лишь дополнительные вычисления для больших массивов. ^[43]

Дробное каскадирование

При дробном каскадировании каждый массив имеет указатели на каждый второй элемент другого массива, поэтому для поиска во всех массивах необходимо выполнить только один двоичный поиск.

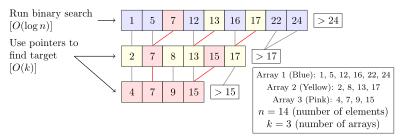
Дробный каскад — это метод, который ускоряет двоичный поиск одного и того же элемента в нескольких отсортированных массивах. Поиск каждого массива отдельно требует времени, где – количество массивов. Дробный каскад сводит это к хранению в каждом массиве конкретной информации о каждом элементе и его положении в других массивах. ^{[46] [47]} ${\textstyle O(k\log n)}$ ${\textstyle k}$ ${\textstyle O(k+\log n)}$

Дробный каскад изначально был разработан для эффективного решения различных задач вычислительной геометрии . Дробный каскад применялся и в других местах, например, в интеллектуальном анализе данных и маршрутизации интернет-протокола . ^[46]

Обобщение на графики

Бинарный поиск был обобщен для работы с определенными типами графов, где целевое значение хранится в вершине, а не в элементе массива. Двоичные деревья поиска являются одним из таких обобщений: когда запрашивается вершина (узел) в дереве, алгоритм либо узнает, что вершина является целью, либо, в противном случае, в каком поддереве будет расположена цель. Однако это можно обобщить следующим образом: следующим образом: учитывая неориентированный, положительно взвешенный граф и целевую вершину, алгоритм при запросе вершины узнает, что она равна целевой, или ему дается инцидентное ребро, которое находится на кратчайшем пути от запрашиваемой вершины к цели. Стандартный алгоритм двоичного поиска — это просто случай, когда граф представляет собой путь. Аналогичным образом, в двоичных деревьях поиска ребра левого или правого поддерева задаются, когда запрашиваемая вершина не равна целевой. Для всех неориентированных графов с положительными весами существует алгоритм, который находит целевую вершину в запросах в худшем случае. ^[48] ${\displaystyle O(\log n)}$

Шумный двоичный поиск

При бинарном поиске с шумом существует определенная вероятность того, что сравнение окажется неверным.

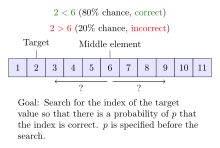
Алгоритмы двоичного поиска с шумом решают случай, когда алгоритм не может надежно сравнить элементы массива. Для каждой пары элементов существует определенная вероятность того, что алгоритм выполнит неправильное сравнение. Шумный двоичный поиск может найти правильное положение цели с заданной вероятностью, которая контролирует надежность полученного положения. Каждая процедура двоичного поиска с шумом должна в среднем выполнять как минимум сравнения, где – функция двоичной энтропии , а – вероятность того, что процедура выдаст неправильную позицию. ^{[49] [50] [51]} Зашумленную задачу двоичного поиска можно рассматривать как случай игры Реньи-Улама , ^[52] как вариант « Двадцати вопросов» , ответы на которые могут быть неправильными. ^[53] ${\displaystyle (1-\tau ){\frac {\log _{2}(n)}{H(p)}}-{\frac {10}{H(p)}}}$ ${\displaystyle H(p)=-p\log _{2}(p)-(1-p)\log _{2}(1-p)}$ ${\displaystyle \tau }$

Квантовый бинарный поиск

Классические компьютеры ограничены наихудшим случаем ровно итераций при выполнении двоичного поиска. Квантовые алгоритмы бинарного поиска по-прежнему ограничены частью запросов (представляющих итерации классической процедуры), но постоянный коэффициент меньше единицы, что обеспечивает меньшую временную сложность на квантовых компьютерах . Любая точная процедура квантового двоичного поиска, то есть процедура, которая всегда дает правильный результат, в худшем случае требует как минимум запросов, где – натуральный логарифм . ^[54] Существует точная квантовая процедура двоичного поиска, которая в худшем случае выполняется в запросах. ^[55] Для сравнения, алгоритм Гровера является оптимальным квантовым алгоритмом для поиска в неупорядоченном списке элементов и требует запросов. ^[56] ${\textstyle \lfloor \log _{2}n+1\rfloor }$ ${\textstyle \log _{2}n}$ ${\textstyle {\frac {1}{\pi }}(\ln n-1)\approx 0.22\log _{2}n}$ ${\textstyle \ln }$ ${\textstyle 4\log _{605}n\approx 0.433\log _{2}n}$ ${\displaystyle O({\sqrt {n}})}$

История

Идея сортировки списка элементов для более быстрого поиска возникла еще в древности. Самым ранним известным примером была табличка Инакибит-Ану из Вавилона, датируемая ок .  200 г. до н.э. Табличка содержала около 500 шестидесятеричных чисел и обратных им чисел , отсортированных в лексикографическом порядке , что облегчало поиск конкретной записи. Кроме того, на Эгейских островах было обнаружено несколько списков имен, отсортированных по первой букве . «Католикон» , латинский словарь, завершенный в 1286 году нашей эры, был первой работой, описывающей правила сортировки слов в алфавитном порядке, а не только по первым нескольким буквам. ^[9]

В 1946 году Джон Мочли впервые упомянул бинарный поиск в рамках лекций Школы Мура , основополагающего курса колледжа по информатике. ^[9] В 1957 году Уильям Уэсли Петерсон опубликовал первый метод интерполяционного поиска. ^{[9] [57]} Каждый опубликованный алгоритм двоичного поиска работал только для массивов, длина которых на единицу меньше степени двойки ^[i] до 1960 года, когда Деррик Генри Лемер опубликовал алгоритм двоичного поиска, который работал на всех массивах. ^[59] В 1962 году Герман Боттенбрух представил реализацию двоичного поиска в Алголе 60 , в которой сравнение на равенство помещалось в конец, увеличивая среднее количество итераций на одну, но уменьшая до одного количество сравнений на итерацию. ^[8] Равномерный бинарный поиск был разработан А.К. Чандрой из Стэнфордского университета в 1971 году. ^[9] В 1986 году Бернар Шазель и Леонидас Дж. Гибас представили дробный каскад как метод решения многочисленных поисковых задач в вычислительной геометрии . ^{[46] [60] [61]}

Проблемы реализации

Хотя основная идея бинарного поиска сравнительно проста, детали могут оказаться на удивление сложными.

-  Дональд Кнут ^[2]

Когда Джон Бентли назвал двоичный поиск проблемой в курсе для профессиональных программистов, он обнаружил, что девяносто процентов не смогли найти правильное решение после нескольких часов работы над ним, главным образом потому, что неправильные реализации не запускались или в редких случаях возвращали неправильный ответ. крайние случаи . ^[62] Исследование, опубликованное в 1988 году, показывает, что точный код для него можно найти только в пяти из двадцати учебников. ^[63] Более того, собственная реализация двоичного поиска Бентли, опубликованная в его книге « Жемчужины программирования» в 1986 году , содержала ошибку переполнения , которая оставалась незамеченной более двадцати лет. Реализация двоичного поиска в библиотеке языка программирования Java имела одну и ту же ошибку переполнения более девяти лет. ^[64]

В практической реализации переменные, используемые для представления индексов, часто будут иметь фиксированный размер (целые числа), и это может привести к арифметическому переполнению для очень больших массивов. Если средняя точка диапазона вычисляется как , то значение может превышать диапазон целых чисел типа данных, используемого для хранения средней точки, даже если и находятся в пределах диапазона. Если и неотрицательны, этого можно избежать, вычислив среднюю точку как . ^[65] ${\displaystyle {\frac {L+R}{2}}}$ ${\displaystyle L+R}$ ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle L}$ ${\displaystyle R}$ ${\displaystyle L+{\frac {R-L}{2}}}$

Бесконечный цикл может возникнуть, если условия выхода из цикла определены неправильно. Если значение превышает , поиск не удался и должен сообщить о неудаче поиска. Кроме того, из цикла необходимо выйти, когда целевой элемент найден, или в случае реализации, в которой эта проверка перенесена в конец, в конце должна присутствовать проверка того, был ли поиск успешным или неудачным. Бентли обнаружил, что большинство программистов, неправильно реализовавших двоичный поиск, допустили ошибку при определении условий выхода. ^{[8] [66]} ${\displaystyle L}$ ${\displaystyle R}$

Библиотечная поддержка

Стандартные библиотеки многих языков включают процедуры двоичного поиска:

• C предоставляет эту функцию bsearch() в своей стандартной библиотеке , которая обычно реализуется посредством двоичного поиска, хотя официальный стандарт этого не требует. ^[67]
• Стандартная библиотека шаблонов C++ предоставляет функции binary_search(), lower_bound()и upper_bound(). ^[68]equal_range()
• Стандартная библиотека Dstd.range Phobos в модуле предоставляет тип SortedRange(возвращаемый функциями sort()и assumeSorted()) с методами contains(), и , которые по умолчанию equaleRange()используют методы двоичного поиска для диапазонов, предлагающих произвольный доступ. ^[69]lowerBound()trisect()
• COBOL предоставляет SEARCH ALLкоманду для выполнения двоичного поиска в упорядоченных таблицах COBOL. ^[70]
• Пакет стандартной библиотеки Gosort содержит функции Search, SearchInts, SearchFloat64sи SearchStrings, которые реализуют общий двоичный поиск, а также специальные реализации для поиска фрагментов целых чисел, чисел с плавающей запятой и строк соответственно. ^[71]
• Java предлагает набор перегруженных binarySearch() статических методов в классах Arraysи Collectionsв стандартном java.utilпакете для выполнения двоичного поиска в массивах Java и в Listмассивах соответственно. ^{[72] [73]}
• Microsoft .NET Framework 2.0 предлагает статические общие версии алгоритма двоичного поиска в своих базовых классах коллекций. Примером может служить System.Arrayметод BinarySearch<T>(T[] array, T value). ^[74]
• Для Objective-C платформа Cocoa предоставляет NSArray -indexOfObject:inSortedRange:options:usingComparator:метод в Mac OS X 10.6+. ^{[75] Фреймворк} Core Foundation C от Apple также содержит CFArrayBSearchValues()функцию. ^[76]
• Python предоставляет bisectмодуль, который сохраняет список в отсортированном порядке без необходимости сортировки списка после каждой вставки. ^[77]
• Класс Array в Rubybsearch включает метод со встроенным приблизительным сопоставлением. ^[78]

Смотрите также

• Метод бисекции  — алгоритм нахождения нуля функции — та же идея, которая используется для решения уравнений в действительных числах.
• Мультипликативный бинарный поиск  — вариант бинарного поиска с упрощенным вычислением средней точки.

Примечания и ссылки

Эта статья была отправлена ​​в WikiJournal of Science на внешнюю академическую рецензию в 2018 году (отчеты рецензента). Обновленный контент был реинтегрирован на страницу Википедии по лицензии CC-BY-SA-3.0 ( 2019 ). Проверенная версия записи: Энтони Лин; и другие. (2 июля 2019 г.). «Алгоритм двоичного поиска» (PDF) . Викижурнал науки . 2 (1): 5. дои : 10.15347/WJS/2019.005. ISSN  2470-6345. Викиданные  Q81434400.

Примечания

1. Обозначение Big O и логарифм . _ В нотации Big O основание логарифма не имеет значения, поскольку каждый логарифм данного основания является постоянным множителем другого логарифма другого основания. То есть , где – константа. ${\displaystyle O}$ ${\displaystyle \log }$ ${\displaystyle \log _{b}(n)=\log _{k}(n)\div \log _{k}(b)}$ ${\displaystyle \log _{k}(b)}$
2. Любой алгоритм поиска, основанный исключительно на сравнениях, может быть представлен с помощью двоичного дерева сравнения. Внутренний путь — это любой путь от корня до существующего узла. Пусть будет длина внутреннего пути , сумма длин всех внутренних путей. Если поиск каждого элемента имеет одинаковую вероятность, средний случай равен или просто единице плюс среднее значение всех длин внутренних путей дерева. Это связано с тем, что внутренние пути представляют собой элементы, которые алгоритм поиска сравнивает с целью. Длины этих внутренних путей представляют собой количество итераций после корневого узла. Добавление среднего значения этих длин к одной итерации в корне дает средний случай. Следовательно, чтобы минимизировать среднее количество сравнений, необходимо минимизировать длину внутреннего пути. Оказывается, дерево двоичного поиска минимизирует длину внутреннего пути. Кнут 1998 доказал, что длина внешнего пути (длина пути по всем узлам, где присутствуют оба дочерних узла для каждого уже существующего узла) минимизируется, когда внешние узлы (узлы без дочерних узлов) лежат в пределах двух последовательных уровней дерева. Это также относится и к внутренним путям, поскольку длина внутреннего пути линейно связана с длиной внешнего пути . Для любого дерева узлов . Когда каждое поддерево имеет одинаковое количество узлов или, что то же самое, массив делится на половины на каждой итерации, внешние узлы, а также их внутренние родительские узлы лежат в пределах двух уровней. Отсюда следует, что двоичный поиск минимизирует количество средних сравнений, поскольку его дерево сравнения имеет минимально возможную длину внутреннего пути. ^[14] ${\displaystyle I}$ ${\displaystyle 1+{\frac {I}{n}}}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle E}$ ${\displaystyle n}$ ${\displaystyle I=E-2n}$
3. Кнут 1998 показал на своей компьютерной модели MIX , которую Кнут спроектировал как изображение обычного компьютера, что среднее время работы этого варианта для успешного поиска составляет единицы времени по сравнению с единицами для обычного двоичного поиска. Временная сложность для этого варианта растет немного медленнее, но за счет более высокой начальной сложности. ^[18] ${\textstyle 17.5\log _{2}n+17}$ ${\textstyle 18\log _{2}n-16}$
4. Кнут 1998 провел формальный анализ производительности обоих алгоритмов поиска по времени. На компьютере Кнута MIX , который Кнут спроектировал как образец обычного компьютера, бинарный поиск занимает в среднем единицы времени для успешного поиска, тогда как линейный поиск с дозорным узлом в конце списка занимает единицы времени. Линейный поиск имеет меньшую начальную сложность, поскольку требует минимальных вычислений, но по сложности он быстро превосходит двоичный поиск. На компьютере MIX бинарный поиск превосходит линейный поиск только с дозорным, если . ^{[14] [23]} ${\textstyle 18\log n-16}$ ${\textstyle 1.75n+8.5-{\frac {n{\text{ mod }}2}{4n}}}$ ${\textstyle n>44}$
5. Вставка значений в отсортированном порядке или в чередующемся ключевом шаблоне с наименьшим и наибольшим значениями приведет к созданию двоичного дерева поиска, которое максимизирует среднее и наихудшее время поиска. ^[28]
6. Можно искать некоторые реализации хэш-таблиц за гарантированное постоянное время. ^[33]
7. Это связано с тем, что простая установка всех битов, на которые указывают хэш-функции для определенного ключа, может повлиять на запросы для других ключей, которые имеют общее хэш-местоположение для одной или нескольких функций. ^[38]
8. Существуют улучшения фильтра Блума, которые повышают его сложность или поддерживают удаление; например, фильтр cuckoo использует хеширование cuckoo для получения этих преимуществ. ^[38]
9. То есть массивы длиной 1, 3, 7, 15, 31... ^[58]

Цитаты

1. Уильямс-младший, Луи Ф. (22 апреля 1976 г.). Модификация метода полуинтервального поиска (двоичного поиска). Материалы 14-й Юго-восточной конференции ACM. АКМ. стр. 95–101. дои : 10.1145/503561.503582 . Архивировано из оригинала 12 марта 2017 года . Проверено 29 июня 2018 г.
2. Knuth 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Двоичный поиск».
3. Баттерфилд и Нгонди 2016, с. 46.
4. Кормен и др. 2009, с. 39.
5. Вайсштейн, Эрик В. «Двоичный поиск». Математический мир .
6. Флорес, Иван; Мадпис, Джордж (1 сентября 1971 г.). «Средняя длина двоичного поиска для плотных упорядоченных списков». Коммуникации АКМ . 14 (9): 602–603. дои : 10.1145/362663.362752 . ISSN  0001-0782. S2CID  43325465.
7. Knuth 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Алгоритм B».
8. Боттенбрух, Герман (1 апреля 1962 г.). «Структура и использование АЛГОЛА 60». Журнал АКМ . 9 (2): 161–221. дои : 10.1145/321119.321120 . ISSN  0004-5411. S2CID  13406983.Процедура описана на стр. 214 (§43), под названием «Программа двоичного поиска».
9. Knuth 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «История и библиография».
10. Касахара и Моришита 2006, стр. 8–9.
11. Sedgewick & Wayne 2011, §3.1, подраздел «Ранг и выбор».
12. Goldman & Goldman 2008, стр. 461–463.
13. Sedgewick & Wayne 2011, §3.1, подраздел «Запросы диапазона».
14. Knuth 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Дальнейший анализ двоичного поиска».
15. Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»), «Теорема B».
16. Чанг 2003, с. 169.
17. Кнут 1997, §2.3.4.5 («Длина пути»).
18. Knuth 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Упражнение 23».
19. Рольф, Тимоти Дж. (1997). «Аналитический вывод сравнений при двоичном поиске». Информационный бюллетень ACM SIGNUM . 32 (4): 15–19. дои : 10.1145/289251.289255 . S2CID  23752485.
20. Хуонг, Пол-Вирак; Морен, Пэт (2017). «Макеты массивов для поиска на основе сравнения». Журнал экспериментальной алгоритмики . 22 . Статья 1.3. arXiv : 1509.05053 . дои : 10.1145/3053370. S2CID  23752485.
21. Кнут 1997, §2.2.2 («Последовательное распределение»).
22. Бим, Пол; Фич, Фейт Э. (2001). «Оптимальные границы для проблемы предшественника и связанных с ней проблем». Журнал компьютерных и системных наук . 65 (1): 38–72. дои : 10.1006/jcss.2002.1822 .
23. Кнут 1998, Ответы на упражнения (§6.2.1) для «Упражнения 5».
24. Кнут 1998, §6.2.1 («Поиск упорядоченной таблицы»).
25. Кнут 1998, §5.3.1 («Сортировка по минимальному сравнению»).
26. Sedgewick & Wayne 2011, §3.2 («Таблицы упорядоченных символов»).
27. Sedgewick & Wayne 2011, §3.2 («Двоичные деревья поиска»), подраздел «Методы и удаление на основе порядка».
28. Кнут 1998, §6.2.2 («Поиск в двоичном дереве»), подраздел «А как насчет худшего случая?».
29. Sedgewick & Wayne 2011, §3.5 («Приложения»), «Какую реализацию таблицы символов мне следует использовать?».
30. Кнут 1998, §5.4.9 («Диски и барабаны»).
31. Кнут 1998, §6.2.4 («Многосторонние деревья»).
32. Кнут 1998, §6.4 («Хеширование»).
33. Кнут 1998, §6.4 («Хеширование»), подраздел «История».
34. Дитцфельбингер, Мартин; Карлин, Анна ; Мельхорн, Курт ; Мейер ауф дер Хайде, Фридхельм; Ронерт, Ганс; Тарьян, Роберт Э. (август 1994 г.). «Динамическое идеальное хеширование: верхняя и нижняя границы». SIAM Journal по вычислительной технике . 23 (4): 738–761. дои : 10.1137/S0097539791194094.
35. Морен, Пэт. «Хеш-таблицы» (PDF) . п. 1. Архивировано (PDF) оригинала 9 октября 2022 г. Проверено 28 марта 2016 г.
36. Кнут 2011, §7.1.3 («Побитовые приемы и методы»).
37. Silverstein, Alan, Judy IV, руководство по эксплуатации (PDF) , Hewlett-Packard , стр. 80–81, заархивировано (PDF) из оригинала 9 октября 2022 г.
38. Фан, Бин; Андерсен, Дэйв Г.; Каминский, Майкл; Митценмахер, Майкл Д. (2014). Фильтр «Кукушка»: практически лучше, чем у Bloom . Материалы 10-й Международной конференции ACM по новым сетевым экспериментам и технологиям. стр. 75–88. дои : 10.1145/2674005.2674994 .
39. Блум, Бертон Х. (1970). «Компромисс пространства и времени при хэш-кодировании с допустимыми ошибками». Коммуникации АКМ . 13 (7): 422–426. CiteSeerX 10.1.1.641.9096 . дои : 10.1145/362686.362692. S2CID  7931252. 
40. Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Важный вариант».
41. Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Алгоритм U».
42. Моффат и Терпин 2002, с. 33.
43. Knuth 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Интерполяционный поиск».
44. Кнут 1998, §6.2.1 («Поиск в упорядоченной таблице»), подраздел «Упражнение 22».
45. Перл, Иегошуа; Итай, Алон; Авни, Хаим (1978). «Интерполяционный поиск — поиск по журналу и по журналу». Коммуникации АКМ . 21 (7): 550–553. дои : 10.1145/359545.359557 . S2CID  11089655.
46. Шазель, Бернар ; Лю, Дин (6 июля 2001 г.). Нижние границы для поиска пересечений и дробного каскадирования в более высоком измерении. 33-й симпозиум ACM по теории вычислений . АКМ. стр. 322–329. дои : 10.1145/380752.380818. ISBN 978-1-58113-349-3. Проверено 30 июня 2018 г.
47. Шазель, Бернар ; Лю, Дин (1 марта 2004 г.). «Нижние границы для поиска пересечений и дробного каскадирования в высших измерениях» (PDF) . Журнал компьютерных и системных наук . 68 (2): 269–284. CiteSeerX 10.1.1.298.7772 . дои : 10.1016/j.jcss.2003.07.003. ISSN  0022-0000. Архивировано (PDF) из оригинала 9 октября 2022 года . Проверено 30 июня 2018 г. 
48. Эмамджоме-Заде, Эхсан; Кемпе, Дэвид; Сингхал, Викрант (2016). Детерминированный и вероятностный бинарный поиск по графам . 48-й симпозиум ACM по теории вычислений . стр. 519–532. arXiv : 1503.00805 . дои : 10.1145/2897518.2897656.
49. Бен-Ор, Майкл; Хасидим, Авинатан (2008). «Байесовский обучающий алгоритм оптимален для шумного двоичного поиска (а также очень хорош для квантового поиска)» (PDF) . 49-й симпозиум по основам информатики . стр. 221–230. дои : 10.1109/FOCS.2008.58. ISBN 978-0-7695-3436-7. Архивировано (PDF) из оригинала 9 октября 2022 года.
50. Пелц, Анджей (1989). «Поиск с известной вероятностью ошибки». Теоретическая информатика . 63 (2): 185–202. дои : 10.1016/0304-3975(89)90077-7 .
51. Ривест, Рональд Л .; Мейер, Альберт Р .; Клейтман, Дэниел Дж .; Винклманн, К. Борьба с ошибками в процедурах двоичного поиска . 10-й симпозиум ACM по теории вычислений . дои : 10.1145/800133.804351 .
52. Пелц, Анджей (2002). «Поиск игр с ошибками — пятьдесят лет борьбы с лжецами». Теоретическая информатика . 270 (1–2): 71–109. дои : 10.1016/S0304-3975(01)00303-6 .
53. Реньи, Альфред (1961). «Об одной задаче теории информации». Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei (на венгерском языке). 6 : 505–516. МР  0143666.
54. Хойер, Питер; Неербек, Ян; Ши, Яоюнь (2002). «Квантовые сложности упорядоченного поиска, сортировки и различения элементов». Алгоритмика . 34 (4): 429–448. arXiv : Quant-ph/0102078 . дои : 10.1007/s00453-002-0976-3. S2CID  13717616.
55. Чайлдс, Эндрю М.; Ландал, Эндрю Дж.; Паррило, Пабло А. (2007). «Квантовые алгоритмы для задачи упорядоченного поиска посредством полуопределенного программирования». Физический обзор А. 75 (3). 032335. arXiv : quant-ph/0608161 . Бибкод : 2007PhRvA..75c2335C. doi : 10.1103/PhysRevA.75.032335. S2CID  41539957.
56. Гровер, Лов К. (1996). Быстрый квантово-механический алгоритм поиска в базе данных . 28-й симпозиум ACM по теории вычислений . Филадельфия, Пенсильвания. стр. 212–219. arXiv : Quant-ph/9605043 . дои : 10.1145/237814.237866.
57. Петерсон, Уильям Уэсли (1957). «Адресация для оперативного хранилища». Журнал исследований и разработок IBM . 1 (2): 130–146. дои : 10.1147/рд.12.0130.
58. «2 ^п -1». OEIS A000225. Архивировано 8 июня 2016 года в Wayback Machine . Проверено 7 мая 2016 г.
59. Лемер, Деррик (1960). «Обучение компьютеру комбинаторным трюкам». Материалы симпозиумов по прикладной математике . 10 : 180–181. дои : 10.1090/psapm/010 . ISBN 9780821813102.
60. Шазель, Бернар ; Гибас, Леонидас Дж. (1986). «Дробный каскад: I. Техника структурирования данных» (PDF) . Алгоритмика . 1 (1–4): 133–162. CiteSeerX 10.1.1.117.8349 . дои : 10.1007/BF01840440. S2CID  12745042. 
61. Шазель, Бернар ; Гибас, Леонидас Дж. (1986), «Дробный каскад: II. Приложения» (PDF) , Algorithmica , 1 (1–4): 163–191, doi : 10.1007/BF01840441, S2CID  11232235
62. Bentley 2000, §4.1 («Проблема двоичного поиска»).
63. Паттис, Ричард Э. (1988). «Ошибки учебника при двоичном поиске». Бюллетень SIGCSE . 20 : 190–194. дои : 10.1145/52965.53012.
64. Блох, Джошуа (2 июня 2006 г.). «Дополнительно, дополнительно – прочитайте об этом все: почти все двоичные поиски и сортировки слиянием не работают». Блог исследований Google . Архивировано из оригинала 1 апреля 2016 года . Проверено 21 апреля 2016 г.
65. Руджери, Сальваторе (2003). «О вычислении полусуммы двух целых чисел» (PDF) . Письма об обработке информации . 87 (2): 67–71. CiteSeerX 10.1.1.13.5631 . дои : 10.1016/S0020-0190(03)00263-1. Архивировано (PDF) из оригинала 3 июля 2006 г. Проверено 19 марта 2016 г. 
66. Bentley 2000, §4.4 («Принципы»).
67. «bsearch – двоичный поиск в отсортированной таблице» . Базовые спецификации открытой группы (7-е изд.). Открытая группа . 2013. Архивировано из оригинала 21 марта 2016 года . Проверено 28 марта 2016 г.
68. Страуструп 2013, с. 945.
69. "std.range - Язык программирования D" . dlang.org . Проверено 29 апреля 2020 г.
70. Unisys (2012), Справочное руководство по программированию COBOL ANSI-85 , том. 1, стр. 598–601.
71. «Сортировка пакетов». Язык программирования Go . Архивировано из оригинала 25 апреля 2016 года . Проверено 28 апреля 2016 г.
72. "java.util.Arrays". Документация платформы Java Standard Edition 8 . Корпорация Оракл . Архивировано из оригинала 29 апреля 2016 года . Проверено 1 мая 2016 г.
73. "java.util.Коллекции". Документация платформы Java Standard Edition 8 . Корпорация Оракл . Архивировано из оригинала 23 апреля 2016 года . Проверено 1 мая 2016 г.
74. "Метод List<T>.BinarySearch (T)" . Сеть разработчиков Microsoft . Архивировано из оригинала 7 мая 2016 года . Проверено 10 апреля 2016 г. .
75. _ Библиотека разработчиков Mac . Apple Inc. Архивировано из оригинала 17 апреля 2016 года . Проверено 1 мая 2016 г.
76. _ Библиотека разработчиков Mac . Apple Inc. Архивировано из оригинала 20 апреля 2016 года . Проверено 1 мая 2016 г.
77. «8.6. bisect — Алгоритм деления массива пополам» . Стандартная библиотека Python . Фонд программного обеспечения Python. Архивировано из оригинала 25 марта 2018 года . Проверено 26 марта 2018 г.
78. Фицджеральд 2015, с. 152.

Источники

• Бентли, Джон (2000). Перлы программирования (2-е изд.). Аддисон-Уэсли . ISBN 978-0-201-65788-3.
• Баттерфилд, Эндрю; Нгонди, Джерард Э. (2016). Словарь информатики (7-е изд.). Оксфорд, Великобритания: Издательство Оксфордского университета . ISBN 978-0-19-968897-5.
• Чанг, Ши-Куо (2003). Структуры данных и алгоритмы . Том. 13. Сингапур: World Scientific . ISBN 978-981-238-348-8. {{cite book}}: |work=игнорируется ( помощь )
• Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2009). Введение в алгоритмы (3-е изд.). MIT Press и McGraw-Hill. ISBN 978-0-262-03384-8.
• Фицджеральд, Майкл (2015). Рубиновый карманный справочник . Севастополь, Калифорния: O'Reilly Media . ISBN 978-1-4919-2601-7.
• Голдман, Салли А .; Голдман, Кеннет Дж. (2008). Практическое руководство по структурам данных и алгоритмам с использованием Java . Бока-Ратон, Флорида: CRC Press . ISBN 978-1-58488-455-2.
• Касахара, Масахиро; Моришита, Шиничи (2006). Масштабная обработка последовательности генома . Лондон, Великобритания: Издательство Имперского колледжа. ISBN 978-1-86094-635-6.
• Кнут, Дональд (1997). Фундаментальные алгоритмы . Искусство компьютерного программирования . Том. 1 (3-е изд.). Ридинг, Массачусетс: Addison-Wesley Professional. ISBN 978-0-201-89683-1.
• Кнут, Дональд (1998). Сортировка и поиск . Искусство компьютерного программирования . Том. 3 (2-е изд.). Ридинг, Массачусетс: Addison-Wesley Professional. ISBN 978-0-201-89685-5.
• Кнут, Дональд (2011). Комбинаторные алгоритмы . Искусство компьютерного программирования . Том. 4А (1-е изд.). Ридинг, Массачусетс: Addison-Wesley Professional. ISBN 978-0-201-03804-0.
• Моффат, Алистер; Терпин, Эндрю (2002). Алгоритмы сжатия и кодирования . Гамбург, Германия: Академическое издательство Kluwer. дои : 10.1007/978-1-4615-0935-6. ISBN 978-0-7923-7668-2.
• Седжвик, Роберт ; Уэйн, Кевин (2011). Алгоритмы (4-е изд.). Река Аппер-Сэддл, Нью-Джерси: Addison-Wesley Professional. ISBN 978-0-321-57351-3.Сокращенная веб-версия; книжная версия.
• Страуструп, Бьярне (2013). Язык программирования C++ (4-е изд.). Река Аппер-Сэддл, Нью-Джерси: Addison-Wesley Professional. ISBN 978-0-321-56384-2.

Внешние ссылки

• Словарь алгоритмов и структур данных NIST: двоичный поиск
• Сравнения и тесты различных реализаций двоичного поиска на C. Архивировано 25 сентября 2019 г. на Wayback Machine.