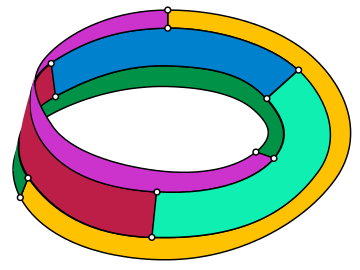
В математической области теории графов граф Титце — это неориентированный кубический граф с 12 вершинами и 18 рёбрами. Он назван в честь Генриха Франца Фридриха Титце , который в 1910 году показал, что ленту Мёбиуса можно разделить на шесть областей, которые все касаются друг друга — три вдоль границы ленты и три вдоль её центральной линии — и, следовательно, для графов, вложенных в ленту Мёбиуса, может потребоваться шесть цветов . [1] Граничные сегменты областей подразделения Титце (включая сегменты вдоль границы самой ленты Мёбиуса) образуют вложение графа Титце.
Граф Титце может быть образован из графа Петерсена путем замены одной из его вершин треугольником. [2] [3] Подобно графу Титце, граф Петерсена образует границу шести взаимно касающихся областей, но на проективной плоскости, а не на ленте Мёбиуса. Если вырезать отверстие из этого подразделения проективной плоскости, окружающего одну вершину, окруженная вершина заменяется треугольником границ областей вокруг отверстия, давая ранее описанную конструкцию графа Титце.
Граф Титце и граф Петерсена являются максимально негамильтоновыми : они не имеют гамильтонова цикла , но любые две несмежных вершины могут быть соединены гамильтоновым путем . [2] Граф Титце и граф Петерсена являются единственными кубическими негамильтоновыми графами с 2 вершинами, связанными между собой , с 12 или менее вершинами. [4]
В отличие от графа Петерсена, граф Титце не является гипогамильтоновым : удаление одной из его трех треугольных вершин образует меньший граф, который остается негамильтоновым.
Раскраска рёбер графа Титце требует четырёх цветов; то есть его хроматический индекс равен 4. Эквивалентно, рёбра графа Титце можно разбить на четыре паросочетания , но не меньше.
Граф Титце соответствует части определения снарка : это кубический граф без мостов , который не является 3-рёберно-раскрашиваемым. Однако большинство авторов ограничивают снарки графами без 3-циклов, поэтому граф Титце обычно не считается снарком. Тем не менее, он изоморфен графу J 3 , части бесконечного семейства цветочных снарков, представленных Р. Айзексом в 1975 году. [5]
В отличие от графа Петерсена, граф Титце может быть покрыт четырьмя совершенными паросочетаниями . Это свойство играет ключевую роль в доказательстве того, что проверка того, может ли граф быть покрыт четырьмя совершенными паросочетаниями, является NP-полной . [6]
Граф Титце имеет хроматическое число 3, хроматический индекс 4, обхват 3 и диаметр 3. Число независимости равно 5. Его группа автоморфизмов имеет порядок 12 и изоморфна диэдральной группе D 6 , группе симметрий правильного шестиугольника ( включая как вращения, так и отражения). Эта группа имеет две орбиты размера 3 и одну размера 6 на вершинах, и, таким образом, этот граф не является вершинно-транзитивным .