Функция одностороннего сжатия

В криптографии односторонняя функция сжатия — это функция, которая преобразует два входа фиксированной длины в выход фиксированной длины. ^[1] Преобразование является «односторонним» , что означает, что для конкретного выхода сложно вычислить входы, которые сжимаются до этого выхода. Односторонние функции сжатия не связаны с обычными алгоритмами сжатия данных , которые вместо этого могут быть инвертированы точно (сжатие без потерь) или приблизительно (сжатие с потерями) к исходным данным.

Односторонние функции сжатия используются, например, в конструкции Меркла–Дамгарда внутри криптографических хеш-функций .

Односторонние функции сжатия часто строятся из блочных шифров . Некоторые методы превращения любого обычного блочного шифра в одностороннюю функцию сжатия — это Davies–Meyer , Matyas–Meyer–Oseas , Miyaguchi–Preneel (функции сжатия с длиной одного блока) и MDC-2/Meyer–Schilling , MDC-4 , Hirose (функции сжатия с длиной двух блоков). Эти методы подробно описаны ниже. ( MDC-2 также является названием хэш-функции, запатентованной IBM .)

Другой метод — 2BOW (или NBOW в целом), который представляет собой «высокоскоростную многоблочную хэш-функцию на основе блочных шифров» ^[1] и обычно достигает (асимптотических) скоростей от 1 до 2 независимо от размера хэша (только с небольшими постоянными накладными расходами). Этот метод еще не подвергался серьезному анализу безопасности, поэтому с ним следует обращаться осторожно.

Сжатие

Функция сжатия смешивает два фиксированных входных данных и создает один фиксированный выходной сигнал того же размера, что и один из входных данных. Это также можно рассматривать как то, что функция сжатия преобразует один большой фиксированный входной сигнал в более короткий фиксированный выходной сигнал.

Например, вход A может быть 128 бит, вход B 128 бит, и они сжимаются вместе в один выход 128 бит. Это эквивалентно тому, что один 256-битный вход сжимается в один выход 128 бит.

Некоторые функции сжатия не сжимают вдвое, а сжимают на какой-то другой фактор. Например, вход A может быть 256 бит, а вход B 128 бит, которые сжимаются в один выход из 128 бит. То есть, в общей сложности 384 входных бита сжимаются вместе в 128 выходных бит.

Смешивание производится таким образом, что достигается полный лавинный эффект . То есть каждый выходной бит зависит от каждого входного бита.

В одну сторону

Односторонняя функция — это функция, которую легко вычислить, но трудно инвертировать. Односторонняя функция сжатия (также называемая хэш-функцией) должна иметь следующие свойства:

Легко вычислить: если у вас есть некоторые входные данные, то легко рассчитать выходные данные.
Сопротивление прообразу: Если злоумышленник знает только выход, то вычислить вход должно быть невозможно. Другими словами, если есть выход , то вычислить вход должно быть невозможно, так что . $ч$ $м$ $\operatorname {хэш} (м)=ч$
Второе сопротивление прообразу: если задан вход, выход которого равен , то должно быть невозможно найти другой вход , который имеет тот же выход , то есть . $m_{1}$ $ч$ $m_{2}$ $ч$ $\operatorname {хэш} (m_{1})=\operatorname {хэш} (m_{2})$
Устойчивость к коллизиям: должно быть сложно найти два разных входа, которые сжимаются до одного и того же выхода, т. е. злоумышленник не должен иметь возможности найти пару сообщений, таких что . Из-за парадокса дней рождения (см. также атака на день рождения ) существует 50% вероятность того, что коллизия может быть найдена за время около , где — количество бит в выходных данных хэш-функции. Таким образом, атака на хэш-функцию не должна иметь возможности найти коллизию с менее чем около работой. $m_{1}\neq m_{2}$ $\operatorname {хэш} (m_{1})=\operatorname {хэш} (m_{2})$ $2^{n/2}$ $n$ $2^{n/2}$

В идеале хотелось бы, чтобы «неосуществимость» в стойкости к прообразу и стойкости ко второму прообразу означала работу примерно где — число бит в выходных данных хэш-функции. Однако, особенно для стойкости к второму прообразу, это сложная проблема. ^[^{необходима цитата}^] $2^{n}$ $n$

Конструкция Меркле – Дамгорда

Распространенное использование односторонних функций сжатия — конструкция Меркла–Дамгарда внутри криптографических хэш-функций. Наиболее широко используемые хэш-функции, включая MD5 , SHA-1 (которая устарела ^[2] ) и SHA-2, используют эту конструкцию.

Функция хэширования должна быть способна преобразовывать сообщение произвольной длины в вывод фиксированной длины. Этого можно добиться, разбив входные данные на ряд блоков одинакового размера и последовательно обрабатывая их с помощью односторонней функции сжатия. Функция сжатия может быть специально разработана для хэширования или построена на основе блочного шифра. Последний обработанный блок также должен быть дополнен длиной , что имеет решающее значение для безопасности этой конструкции.

При применении дополнения длины (также называемого MD-усилением) атаки не могут находить коллизии быстрее, чем парадокс дней рождения ( , размер блока в битах), если используемая функция устойчива к коллизиям. ^[3]^[4] Таким образом, конструкция хэша Меркла–Дамгарда сводит проблему поиска правильной хэш-функции к поиску правильной функции сжатия. $2^{n/2}$ $n$ $f$

Вторая атака на прообраз (при наличии сообщения, которое злоумышленник находит для удовлетворения другим сообщением, может быть выполнена согласно Келси и Шнайеру ^[5] для сообщения -message-block за время . Сложность этой атаки достигает минимума для длинных сообщений, когда и приближается к минимуму, когда сообщения короткие. $m_{1}$ $m_{2}$ $\operatorname {хэш} (m_{1})=\operatorname {хэш} (m_{2})$ $2^{k}$ $k\times 2^{n/2+1}+2^{n-k+1}$ $2^{3n/4+2}$ $k=2^{n/4}$ $2^{n}$

Построение из блочных шифров

Односторонние функции сжатия часто строятся на основе блочных шифров.

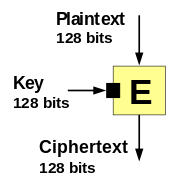
Блочные шифры принимают (как и односторонние функции сжатия) два входных сигнала фиксированного размера ( ключ и открытый текст ) и возвращают один единственный выходной сигнал ( шифротекст ), который имеет тот же размер, что и входной открытый текст.

Однако современные блочные шифры являются лишь частично односторонними. То есть, имея открытый текст и шифротекст, невозможно найти ключ, который зашифрует открытый текст в шифротекст. Но имея шифротекст и ключ, можно найти соответствующий открытый текст, просто используя функцию дешифрования блочного шифра. Таким образом, чтобы превратить блочный шифр в одностороннюю функцию сжатия, необходимо добавить некоторые дополнительные операции.

Некоторые методы превращения любого обычного блочного шифра в одностороннюю функцию сжатия — это Дэвис–Майер, Матьяс–Майер–Осеас, Миягучи–Пренель (функции сжатия с длиной одного блока) и MDC-2, MDC-4, Хиросе (функции сжатия с длиной двух блоков).

Функции сжатия с длиной одного блока выводят то же количество бит, что и обработанное базовым блочным шифром. Следовательно, функции сжатия с длиной двух блоков выводят в два раза большее количество бит.

Если блочный шифр имеет размер блока , скажем, 128 бит, методы с одинарной длиной блока создают хэш-функцию с размером блока 128 бит и производят хэш из 128 бит. Методы с двойной длиной блока создают хэши с удвоенным размером хэша по сравнению с размером блока используемого блочного шифра. Таким образом, 128-битный блочный шифр можно превратить в 256-битную хэш-функцию.

Эти методы затем используются внутри конструкции Меркла–Дамгарда для построения фактической хэш-функции. Эти методы подробно описаны ниже.

Использование блочного шифра для построения односторонней функции сжатия для хэш-функции обычно несколько медленнее, чем использование специально разработанной односторонней функции сжатия в хэш-функции. Это связано с тем, что все известные безопасные конструкции выполняют планирование ключей для каждого блока сообщения. Блэк, Кокран и Шримптон показали, что невозможно построить одностороннюю функцию сжатия, которая делает только один вызов блочного шифра с фиксированным ключом. ^[6] На практике разумные скорости достигаются при условии, что планирование ключей выбранного блочного шифра не является слишком тяжелой операцией.

Но в некоторых случаях это проще, потому что одна реализация блочного шифра может использоваться как для блочного шифра, так и для хэш-функции. Это также может сэкономить место в коде в очень маленьких встроенных системах, таких как, например, смарт-карты или узлы в автомобилях или других машинах.

Таким образом, хэш-скорость или скорость дает представление об эффективности хэш-функции, основанной на определенной функции сжатия. Скорость итерированной хэш-функции описывает соотношение между числом операций блочного шифра и выходными данными. Точнее, скорость представляет собой соотношение между числом обработанных битов ввода , выходной битовой длиной блочного шифра и необходимыми операциями блочного шифра для получения этих выходных битов. Как правило, использование меньшего количества операций блочного шифра приводит к лучшей общей производительности всей хэш-функции, но это также приводит к меньшему значению хэш-функции, что может быть нежелательным. Скорость выражается формулой: $м$ $n$ $с$ $n$

$R_{h}={\frac {\left|m_{i}\right|}{s\cdot n}}$

Функцию хеширования можно считать безопасной только в том случае, если выполняются как минимум следующие условия:

Блочный шифр не имеет особых свойств, отличающих его от идеальных шифров, таких как слабые ключи или ключи, которые приводят к идентичным или связанным шифрованным данным (фиксированные точки или коллизии ключей).
Полученный размер хеша достаточно большой. Согласно атаке на день рождения, желателен уровень безопасности 2 80 (который, как правило, считается невыполнимым для вычисления сегодня) [необходима цитата], поэтому размер хеша должен быть ^не менее ^{160 бит .}
Длина последнего блока должным образом дополняется до хеширования. (См. конструкцию Меркла–Дамгарда .) Дополнение длины обычно реализуется и обрабатывается внутри специализированных хеш-функций, таких как SHA-1 и т. д.

Представленные ниже конструкции: Дэвиса–Мейера, Матьяса–Мейера–Осеаса, Миягучи–Пренеля и Хиросе, как было показано, являются безопасными при анализе черного ящика . ^[7]^[8] Цель состоит в том, чтобы показать, что любая атака, которая может быть найдена, не более эффективна, чем атака дня рождения при определенных предположениях. Модель черного ящика предполагает, что используется блочный шифр, который случайно выбирается из набора, содержащего все соответствующие блочные шифры. В этой модели злоумышленник может свободно шифровать и расшифровывать любые блоки, но не имеет доступа к реализации блочного шифра. Функция шифрования и расшифровки представлена оракулами, которые получают пару либо открытого текста и ключа, либо зашифрованного текста и ключа. Затем оракулы отвечают случайно выбранным открытым текстом или зашифрованным текстом, если пара была запрошена в первый раз. Они оба разделяют таблицу для этих триплетов, пары из запроса и соответствующего ответа, и возвращают запись, если запрос был получен во второй раз. Для доказательства есть алгоритм поиска коллизий, который делает случайно выбранные запросы к оракулам. Алгоритм возвращает 1, если два ответа приводят к коллизии с участием хэш-функции, которая построена из функции сжатия, применяющей этот блочный шифр (0 в противном случае). Вероятность того, что алгоритм вернет 1, зависит от количества запросов, которые определяют уровень безопасности.

Дэвис–Мейер

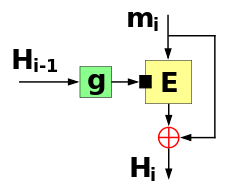
Функция сжатия единичного блока Дэвиса-Майера подает каждый блок сообщения ( ) как ключ к блочному шифру. Она подает предыдущее значение хэша ( ) как открытый текст для шифрования. Затем выходной шифртекст также подвергается операции XOR (⊕) с предыдущим значением хэша ( ) для получения следующего значения хэша ( ). В первом раунде, когда нет предыдущего значения хэша, он использует постоянное заранее заданное начальное значение ( ). $m_{i}$ $H_{i-1}$ $H_{i-1}$ $H_{i}$ $H_{0}$

В математической нотации уравнение Дэвиса–Мейера можно описать следующим образом:

H_{i}=E_{m_{i}}{(H_{i-1})}\oplus {H_{i-1}}

Схема имеет скорость (k — размер ключа):

R_{DM}={\frac {k}{1\cdot n}}={\frac {k}{n}}

Если блочный шифр использует, например, 256-битные ключи, то каждый блок сообщения ( ) представляет собой 256-битный фрагмент сообщения. Если тот же блочный шифр использует размер блока 128 бит, то входные и выходные хеш-значения в каждом раунде составляют 128 бит. $m_{i}$

Вариации этого метода заменяют XOR любой другой групповой операцией, например, сложением 32-битных беззнаковых целых чисел.

Примечательным свойством конструкции Дэвиса–Майера является то, что даже если базовый блочный шифр полностью безопасен, возможно вычислить фиксированные точки для конструкции: для любого можно найти значение такое, что : нужно просто установить . ^[9] Это свойство, которым случайные функции, безусловно, не обладают. До сих пор ни одна практическая атака не была основана на этом свойстве, но следует знать об этой «особенности». Фиксированные точки могут быть использованы во второй атаке прообраза (при наличии сообщения , злоумышленник находит другое сообщение для удовлетворения ) Келси и Шнайера ^[5] для сообщения -message-block за время . Если конструкция не позволяет легко создавать фиксированные точки (например, Matyas–Meyer–Oseas или Miyaguchi–Preneel), то эта атака может быть выполнена за время. В обоих случаях сложность выше, но ниже , когда сообщения длинные, и что, когда сообщения становятся короче, сложность атаки приближается к . $м$ $ч$ $E_{m}(h)\oplus h=h$ $h=E_{м}^{-1}(0)$ $m_{1}$ $m_{2}$ $\operatorname {хэш} (m_{1})=\operatorname {хэш} (m_{2})$ $2^{k}$ $3\times 2^{n/2+1}+2^{n-k+1}$ $k\times 2^{n/2+1}+2^{n-k+1}$ $2^{n/2}$ $2^{n}$ $2^{n}$

Безопасность конструкции Дэвиса–Майера в модели идеального шифра была впервые доказана Р. Винтерницем. ^[10]

Матьяс–Майер–Осеас

Функцию одностороннего сжатия Матиаса–Майера–Осеаса с длиной блока можно считать двойственной (противоположной) функции Дэвиса–Майера.

Он подает каждый блок сообщения ( ) как открытый текст для шифрования. Затем выходной шифртекст также подвергается операции XOR (⊕) с тем же блоком сообщения ( ) для получения следующего значения хэша ( ). Предыдущее значение хэша ( ) подается как ключ к блочному шифру. В первом раунде, когда нет предыдущего значения хэша, он использует постоянное заранее заданное начальное значение ( ). $m_{i}$ $m_{i}$ $H_{i}$ $H_{i-1}$ $H_{0}$

Если блочный шифр имеет разные размеры блока и ключа, то хэш-значение ( ) будет иметь неправильный размер для использования в качестве ключа. Шифр также может иметь другие специальные требования к ключу. Затем хэш-значение сначала проходит через функцию для преобразования/дополнения, чтобы подойти в качестве ключа для шифра. $H_{i-1}$ $г$

В математической нотации уравнение Матьяша–Майера–Осеаса можно описать следующим образом:

H_{i}=E_{g(H_{i-1})}(m_{i})\oplus m_{i}

Схема имеет ставку:

R_{MMO}={\frac {n}{1\cdot n}}=1

Вторая атака прообраза (при наличии сообщения злоумышленник находит другое сообщение для удовлетворения ) может быть выполнена согласно Келси и Шнайеру ^[5] для сообщения -message-block за время . Сложность выше, но ниже, когда сообщения длинные, и что когда сообщения становятся короче, сложность атаки приближается к . $m_{1}$ $m_{2}$ $\operatorname {хэш} (m_{1})=\operatorname {хэш} (m_{2})$ $2^{k}$ $k\times 2^{n/2+1}+2^{n-k+1}$ $2^{n/2}$ $2^{n}$ $2^{n}$

Миягучи–Пренель

Функция сжатия одностороннего блока длины Миягучи–Пренеля является расширенным вариантом функции Матьяса–Майера–Осеаса. Она была независимо предложена Сёдзи Миягучи и Бартом Пренелем .

Он подает каждый блок сообщения ( ) как открытый текст для шифрования. Затем выходной шифртекст подвергается операции XOR (⊕) с тем же блоком сообщения ( ), а затем также подвергается операции XOR с предыдущим значением хеша ( ) для получения следующего значения хеша ( ). Предыдущее значение хеша ( ) подается как ключ к блочному шифру. В первом раунде, когда нет предыдущего значения хеша, он использует постоянное заранее заданное начальное значение ( ). $m_{i}$ $m_{i}$ $H_{i-1}$ $H_{i}$ $H_{i-1}$ $H_{0}$

В математической нотации уравнение Миягути–Пренеля можно описать следующим образом:

H_{i}=E_{g(H_{i-1})}(m_{i})\oplus H_{i-1}\oplus m_{i}

Схема имеет ставку:

R_{MP}={\frac {n}{1\cdot n}}=1

Роли и можно поменять местами, так что шифруется ключом , что делает этот метод расширением метода Дэвиса–Майера. $m_{i}$ $H_{i-1}$ $H_{i-1}$ $m_{i}$

Хиросэ

Односторонняя функция сжатия Hirose ^[8] двойной длины блока состоит из блочного шифра и перестановки . Она была предложена Shoichi Hirose в 2006 году и основана на работе ^[11] Mridul Nandi. $p$

Он использует блочный шифр, длина ключа которого больше длины блока , и создает хэш размером . Например, любой из кандидатов AES с 192- или 256-битным ключом (и 128-битным блоком). $к$ $n$ $2n$

Каждый раунд принимает часть сообщения длиной в биты и использует ее для обновления двухбитных значений состояния и . $m_{i}$ $кн$ $n$ $G$ $H$

Сначала объединяется с для создания ключа . Затем два значения обратной связи обновляются в соответствии с: $m_{i}$ $H_{i-1}$ $K_{i}$

$G_{i}=E_{K_{i}}(G_{i-1})\oplus G_{i-1}$
$H_{i}=E_{K_{i}}(p(G_{i-1}))\oplus p(G_{i-1})$

$p(G_{i-1})$ — произвольная перестановка без фиксированной точки для -битного значения, обычно определяемая как для произвольной ненулевой константы (все единицы могут быть удобным выбором). $n$ $p(x)=x\oplus c$ $с$

Каждое шифрование напоминает стандартную конструкцию Дэвиса–Майера. Преимущество этой схемы перед другими предлагаемыми схемами с двойной длиной блока заключается в том, что оба шифрования используют один и тот же ключ, и, таким образом, усилия по планированию ключей могут быть разделены.

Окончательный вывод — . Схема имеет скорость относительно шифрования сообщения с помощью шифра. $H_{t}||G_{t}$ ${\textstyle R_{Хиросе}={\frac {kn}{2n}}}$

Хиросе также приводит доказательство в модели идеального шифра.

Губчатая конструкция

Губчатую конструкцию можно использовать для построения функций одностороннего сжатия.

Смотрите также

Whirlpool — криптографическая хеш-функция, построенная с использованием конструкции Миягути–Пренеля и блочного шифра, похожего на Square и AES .
CBC-MAC , OMAC и PMAC — методы преобразования блочных шифров в коды аутентификации сообщений (MAC).

Ссылки

Цитаты

^ ab Handbook of Applied Cryptography Альфреда Дж. Менезеса, Пола К. ван Ооршота, Скотта А. Ванстоуна. Пятое издание (август 2001 г.), стр. 328.
^ "Объявление о первой коллизии SHA1". Блог Google Online Security . Получено 2020-01-12 .
^ Иван Дамгард. Принцип проектирования хэш-функций. В книге Жиля Брассара, редактора CRYPTO, том 435 LNCS, страницы 416–427. Springer, 1989.
^ Ральф Меркл. Односторонние хэш-функции и DES. В книге Жиля Брассара, редактора CRYPTO, том 435 LNCS, страницы 428–446. Springer, 1989.
^ abcd Джон Келси и Брюс Шнайер. Вторые прообразы на n-битных хэш-функциях для гораздо меньших, чем 2n, работ. В Рональде Крамере, редакторе, EUROCRYPT, том 3494 LNCS, страницы 474–490. Springer, 2005.
^ Джон Блэк, Мартин Кокран и Томас Шримптон. О невозможности высокоэффективных хэш-функций на основе блочного шифра. Достижения в криптологии – EUROCRYPT '05, Орхус, Дания, 2005. Авторы определяют хэш-функцию как «высокоэффективную, если ее функция сжатия использует ровно один вызов блочного шифра, ключ которого фиксирован».
^ Джон Блэк, Филлип Рогауэй и Том Шримптон. Анализ черного ящика конструкций блочных шифров на основе хэш-функций из PGV. Advances in Cryptology – CRYPTO '02, Lecture Notes in Computer Science, т. 2442, стр. 320–335, Springer, 2002. См. таблицу на стр. 3, Davies–Meyer, Matyas–Meyer–Oseas и Miyaguchi–Preneel пронумерованы в первом столбце как хэш-функции 5, 1 и 3.
^ ab S. Hirose, Некоторые правдоподобные конструкции хэш-функций двойной длины блока . В: Robshaw, MJB (ред.) FSE 2006, LNCS, т. 4047, стр. 210–225, Springer, Heidelberg 2006.
↑ Справочник по прикладной криптографии Альфреда Дж. Менезеса, Пола К. ван Ооршота, Скотта А. Ванстоуна. Пятое издание (август 2001 г.), стр. 375.
^ Р. Винтерниц. Безопасная односторонняя хэш-функция, построенная на основе DES. В трудах симпозиума IEEE по информационной безопасности и конфиденциальности, стр. 88-90. IEEE Press, 1984.
^ М. Нанди, На пути к оптимальным хэш-функциям двойной длины , в: Труды 6-й Международной конференции по криптологии в Индии (INDOCRYPT 2005), Конспект лекций по информатике 3797, страницы 77–89, 2005.

Источники

Менезес; ван Ооршот; Ванстоун (2001). "Хэш-функции и целостность данных" (PDF) . Справочник по прикладной криптографии.