stringtranslate.com

Комбинаторность

В музыке, использующей двенадцатитоновую технику , комбинаторность — это качество, присущее двенадцатитоновым тоновым рядам , при котором каждая секция ряда и пропорциональное число ее преобразований объединяются, образуя агрегаты (все двенадцать тонов). [1] Так же, как высоты тона агрегата, созданного тоновым рядом, не обязательно должны возникать одновременно, высоты тона комбинаторно созданного агрегата не обязательно должны возникать одновременно. Арнольд Шенберг , создатель двенадцатитоновой техники, часто объединял P-0/I-5, чтобы создать «два агрегата, между первыми гексахордами каждого и вторыми гексахордами каждого соответственно». [1]

Комбинаторность — побочный эффект производных рядов , где начальный сегмент или набор может быть объединен с его преобразованиями (T, R, I, RI) для создания целого ряда. «Вывод относится к процессу, посредством которого, например, начальный трихорд ряда может быть использован для получения нового, «производного» ряда путем применения стандартных двенадцатитоновых операций транспозиции , инверсии , ретроградности и ретроградной инверсии ». [2]

Комбинаторные свойства зависят не от порядка нот в наборе, а только от содержания набора, и комбинаторность может существовать между тремя тетрахордовыми и между четырьмя трихордовыми наборами , а также между парами гексахордов [3] и шестью диадами [4] . Дополнение в этом контексте — это половина комбинаторного набора классов высоты тона, и в большинстве случаев это «другая половина» любой пары, включая наборы классов высоты тона, текстуры или диапазон высоты тона.

Определение

В самом общем смысле комплементарность — это разделение коллекций классов высоты тона на два дополнительных набора, один из которых содержит классы высоты тона, отсутствующие в другом. [1] Более строго комплементарность — это «процесс объединения сущностей по обе стороны от центра симметрии». [5]

Комбинаторные ряды тонов из «Моисея и Арона» Арнольда Шёнберга, объединяющие дополнительные гексахорды из P-0/I-3 [6]

Термин «комбинаторный», по-видимому, был впервые применен к двенадцатитоновой музыке Милтоном Бэббитом в 1950 году [7] , когда он опубликовал обзор книг Рене Лейбовица «Шенберг и его школа» и «Что такое музыка двадцати сыновей?» [8]. Бэббит также ввел термин «производный ряд» . [2]

Гексахордальная комбинаторность

Комбинаторные трихордовые гексахорды из Фортепианного концерта Эллиотта Картера , т. 59–60 [9]

12-тоновый ряд имеет гексахордальную комбинаторность с другим 12-тоновым рядом, если их соответствующие первые (а также вторые, поскольку 12-тоновый ряд сам по себе по определению образует совокупность) гексахорды образуют совокупность.

Существует четыре основных типа комбинаторности. Гексахорд может быть:

и таким образом:

Первичная (транспозиционная) комбинаторность гексахорда относится к свойству гексахорда, посредством которого он образует агрегат с одной или несколькими своими транспозициями. Альтернативно, транспозиционная комбинаторность — это отсутствие общих классов высоты тона между гексахордом и одной или несколькими его транспозициями. Например, 0 2 4 6 8 t и его транспозиция на один полутон (+1): 1 3 5 7 9 e, не имеют общих нот.

Ретроградная гексахордовая комбинаторность считается тривиальной, поскольку любой ряд имеет ретроградную гексахордовую комбинаторность с самим собой ( все ряды тонов имеют ретроградную комбинаторность).

Инверсионная комбинаторность — это связь между двумя рядами, основным рядом и его инверсией. Первая половина основного ряда, или шесть нот, являются последними шестью нотами инверсии, хотя и не обязательно в том же порядке. Таким образом, первая половина каждого ряда является дополнением другого . Тот же вывод применим и ко второй половине каждого ряда. При объединении эти ряды по-прежнему сохраняют полностью хроматическое ощущение и не имеют тенденции усиливать определенные высоты как тональные центры, как это могло бы произойти со свободно объединенными рядами. Например, ряд из «Моисея и Арона» Шенберга , выше, содержит: 0 1 4 5 6 7, это инвертируется в: 0 e 8 7 6 5, добавьте три = 2 3 8 9 t e.

01 4567 : 1-й гексахорд P0/2-й гексахорд I3 23 89te : 2-й гексахорд P0/1-й гексахорд I3полная хроматическая гамма

Ретроградно-инверсионная комбинаторность — это отсутствие общих высот между гексахордами ряда и его ретроградно-инверсионным рядом.

Бэббит также описал полукомбинаторный ряд и чисто комбинаторный ряд, причем последний представляет собой ряд, который является комбинаторным с любым из его производных и их транспозициями.Полукомбинаторные множества — это множества, гексахорды которых способны образовывать агрегат с одним из его основных преобразований (R, I, RI), транспонированным. Существует тринадцать гексахордов, которые являются полукомбинаторными только по инверсии. 

(0) 0 1 2 3 4 6 // эт 9 8 7 5(1) 0 1 2 3 5 7 // эт 9 8 6 4(2) 0 1 2 3 6 7 // эт 9 8 5 4(3) 0 1 2 4 5 8 // эт 9 7 6 3(4) 0 1 2 4 6 8 // эт 9 7 5 3(5) 0 1 2 5 7 8 // эт 9 6 4 3(6) 0 1 3 4 6 9 // и т.д. 8 7 5 2(7) 0 1 3 5 7 9 // и т.д. 8 6 4 2(8) 0 1 3 5 8 9 // 7 6 4 2 и т.д.(9) 0 1 3 6 7 9 // эт 8 5 4 2(10) 0 1 4 5 6 8 // 3 2 и 9 7(11) 0 2 3 4 6 8 // 1 и 9 7 5(12) 0 2 3 5 7 9 // 1 и 8 6 4

Любой гексахорд, содержащий ноль в своем интервальном векторе, обладает транспозиционной комбинаторностью (другими словами: для достижения комбинаторности гексахорд не может быть транспонирован на интервал, равный содержащейся в нем ноте). Например, существует один гексахорд, который является комбинаторным по транспозиции (T6):

(0) 0 1 3 4 5 8 // 6 7 9 те 2

Ни один из гексахордов не содержит тритонов.

Основной первый порядок полностью комбинаторного ряда тонов Группена, хотя это свойство не используется композиционно в этой работе. [ 10 ]
Гексахорд «Ода Наполеону» [11] в простой форме [12] Один из шести полностью комбинаторных «исходных наборов» гексахордов Бэббита. [12]

Все-комбинаторные множества — это множества, чьи гексахорды способны образовывать агрегат с любым из его основных преобразований, транспонированных. Существует шесть исходных множеств, или базовых гексахордально все-комбинаторных множеств, каждый гексахорд которых может быть переупорядочен внутри себя:

(А) 0 1 2 3 4 5 // 6 7 8 9 те(Б) 0 2 3 4 5 7 // 6 8 9 те 1(С) 0 2 4 5 7 9 // 6 8 те 1 3(Д) 0 1 2 6 7 8 // 3 4 5 9 те(Э) 0 1 4 5 8 9 // 2 3 6 7 те(Ф) 0 2 4 6 8 т // 1 3 5 7 9 е

Примечание: t = 10, e = 11.

Поскольку первые три набора ( A , B и C ) удовлетворяют всем четырем критериям только для одного транспозиционного значения, набор D удовлетворяет им для двух транспозиционных значений, E для трех значений и F для шести транспозиций, Баббитт обозначает эти четыре группы как «первого порядка», «второго порядка», «третьего порядка» и «шестого порядка» полностью комбинаторные гексахорды соответственно. [13] Обратите внимание, что первый набор, набор «A», представляет собой первые шесть нот восходящей хроматической гаммы, а последний набор, набор «F», представляет собой целотонный строй. [14]

Комбинаторность может использоваться для создания совокупности всех двенадцати тонов, хотя этот термин часто относится просто к комбинаторным рядам, указанным вместе.

Гексахордовая комбинаторность — это концепция в посттональной теории, описывающая комбинацию гексахордов, часто используемая в отношении музыки Второй венской школы . В музыке, которая последовательно использует все двенадцать хроматических тонов (особенно в двенадцатитоновой и последовательной музыке ), агрегат (совокупность всех 12 классов высоты тона) может быть разделена на два гексахорда (совокупности из 6 высот). Это разбивает агрегат на две меньшие части, что упрощает последовательность нот, переход между рядами или агрегатами и объединение нот и агрегатов.

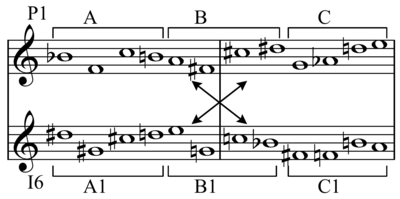
Основные формы, P1 и I6, фортепианной пьесы Шёнберга , соч. 33а, тоновый ряд характеризуются гексахордовой комбинаториальностью и содержат по три чистых квинты каждая, что является соотношением между P1 и I6. [15]

Иногда гексахорд может быть объединен с его инвертированной или транспонированной версией в особом случае, что затем приведет к образованию совокупности (полного набора из 12 хроматических тонов).

Ряд (B ♭ =0: 0 6 8 5 7 e 4 3 9 t 1 2), используемый Шёнбергом, можно разделить на два гексахорда:

Б ♭ ЭФ ♯ Э ♭ ФА // ДЦ ♯ СГ ♯ БК

Если инвертировать первый гексахорд и транспонировать его, получится следующий гексахорд, представляющий собой перестановку второго гексахорда:

GC ♯ BDCG ♯ = DC ♯ GG ♯ BC

Таким образом, когда вы накладываете исходный гексахорд 1 (P0) на транспонированную инверсию гексахорда 1 (в данном случае I9), получается полный набор из 12 тонов. Если бы вы продолжили остаток транспонированного, инвертированного ряда (I9) и наложили исходный гексахорд 2, вы бы снова получили полный набор из 12 хроматических тонов.

В «Вариациях для оркестра» Шёнберга , соч. 31, тоновый ряд второй половины P1 имеет те же ноты, но в другом порядке, что и первая половина I10: «Таким образом, можно использовать P1 и I10 одновременно и в параллельном движении, не вызывая удвоения нот». [16]

Гексахордовая комбинаторность тесно связана с теорией 44 тропов , созданной Йозефом Маттиасом Хауэром в 1921 году, хотя, кажется, Хауэр вообще не оказал влияния на Баббитта. Более того, мало доказательств, указывающих на то, что Хауэр обладал обширными знаниями об инверсионных свойствах тропов по крайней мере до 1942 года. [17] Однако самые ранние записи о комбинаторных отношениях гексахордов можно найти среди теоретических трудов австрийского композитора и теоретика музыки Отмара Штайнбауэра . [a] Он провел подробные исследования системы тропов в начале 1930-х годов, которые задокументированы в неопубликованной машинописной рукописи Klang- und Meloslehre (1932). Материалы Штейнбауэра, датированные 1932 и 1934 годами, содержат исчерпывающие данные о комбинаторных трихордах, тетрахордах и гексахордах, включая полукомбинаторные и полностью комбинаторные наборы. Поэтому они могут быть самыми ранними записями в истории музыки. [18] Сборник морфологических материалов Штейнбауэра частично стал общедоступным в 1960 году вместе с его скриптом Lehrbuch der Klangreihenkomposition (авторское издание) и был переиздан в 2001 году. [19]

Трихордальная комбинаторность

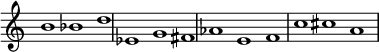
{ #(set-global-staff-size 18) \override Score.TimeSignature #'stencil = ##f \override Score.SpacingSpanner.strict-note-spacing = ##t \set Score.proportionalNotationDuration = #(ly:make-moment 2/1) \relative c'' { \time 3/1 \set Score.tempoHideNote = ##t \tempo 1 = 60 b1 bes d es, g fis aes ef c' cis a } }
Ряд тонов для Концерта для девяти инструментов соч. 24 Веберна . Полностью комбинаторный производный ряд, состоящий из четырех трихордов : P RI R I.

Трихордальная комбинаторность — это способность ряда образовывать агрегаты посредством объединения трихорд. «Трихордальная комбинаторность подразумевает одновременное представление четырех рядов в пакетах из трех штук». [20] Существование трихордальной комбинаторности или любой другой формы в ряду не исключает существования других форм комбинаторности (по крайней мере, тривиальная гексахордальная комбинаторность существует между каждой формой ряда и ее ретроградом). Все трихордально полученные ряды обладают трихордальной комбинаторностью.

Примечания

  1. ^ Штайнбауэр (1895–1962) был бывшим учеником Арнольда Шёнберга и Йозефа Маттиаса Хауэра. См. статью о Штайнбауэре на de.wikipedia.org.

Источники

  1. ^ abc Whittall, Arnold . 2008. Кембриджское введение в сериализм. Cambridge Introductions to Music , стр. 272. Нью-Йорк: Cambridge University Press. ISBN  978-0-521-86341-4 (твердый переплет) ISBN 978-0-521-68200-8 (бумажная книга). 
  2. ^ ab Кристенсен, Томас (2002). Кембриджская история западной музыкальной теории , [без пагинации] . Кембридж. ISBN 9781316025482 . 
  3. ↑ Джордж Перл , Серийная композиция и атональность: Введение в музыку Шёнберга, Берга и Веберна , четвертое издание, пересмотренное (Беркли, Лос-Анджелес, Лондон: Издательство Калифорнийского университета, 1977), 129–131. ISBN 0-520-03395-7 
  4. ↑ Питер Вестергаард , «Некоторые проблемы, возникающие в связи с ритмическими процедурами в композиции Милтона Бэббита для двенадцати инструментов », Perspectives of New Music 4, № 1 (осень–зима 1965 г.): 109–118. Цитата по 114.
  5. ^ Килиан-Гилберт, Марианна (1982–83). «Связь симметричных наборов классов высоты тона и метафора полярности Стравинского», Перспективы новой музыки 21: 210. JSTOR  832874.
  6. ^ Уиттолл, 103
  7. ^ Уиттолл, 245n8
  8. ^ Милтон Баббитт , Обзор без названия, Журнал Американского музыковедческого общества 3, № 1 (весна 1950 г.): 57–60. Обсуждение комбинаторности на стр. 60.
  9. ^ Мид, Эндрю (2002). «Двенадцатитоновая композиция и музыка Эллиотта Картера», Концертная музыка, рок и джаз с 1945 года: эссе и аналитические исследования , стр. 80–81. Элизабет Уэст Марвин, Ричард Герман; ред. Университет Рочестера. ISBN 9781580460965 . 
  10. ^ Харви, Джонатан (1975). Музыка Штокхаузена , стр. 56–58. ISBN 0-520-02311-0 . 
  11. ^ Дэвид Левин , «Re: Intervallic Relations Between Two Collections of Notes». Журнал теории музыки 3, № 2 (ноябрь 1959 г.): 298–301. стр. 300.
  12. ^ ab Van den Toorn, Pieter C. (1996). Музыка, политика и академия , стр. 128–129. ISBN 0-520-20116-7 . 
  13. ↑ Джон Ран , Базовая атональная теория , Longman Music Series (Нью-Йорк и Лондон: Longman, 1980): 118.
  14. ^ Кастанеда, Рэмси (март 2016 г.). "All-Combinatorial Hexachords" . Получено 1 июня 2016 г. .
  15. ^ Leeuw, Ton de (2005). Музыка двадцатого века: исследование ее элементов и структуры . Перевод Стивена Тейлора. Амстердам: Amsterdam University Press. С. 155–157. ISBN 90-5356-765-8.Перевод музыки Twintigste Eeuw: een onderzoek naar haar elementen en structuur . Утрехт: Остхук, 1964. Третье впечатление, Утрехт: Бон, Шелтема и Холкема, 1977. ISBN 90-313-0244-9 . 
  16. ^ Леув 2005, стр. 154–155.
  17. ^ Дидерихс, Иоахим. Федоров, Николаус. Швигер, Йоханнес (ред.). 2007. Йозеф Матиас Хауэр: Шрифтен, Манифест, Документы 428–440. Вена: Верлаг Лафит
  18. ^ Седиви, Доминик. 2011. Серийная композиция и тональность. Введение в музыку Хауэра и Штайнбауэра , с. 70. Вена: издание моно/монохром. ISBN 978-3-902796-03-5 . Седиви, Доминик. 2012. Тропентехник. Ihre Anwendung und ihre Möglichkeiten , 258–264. Зальцбургский Штир 5. Вюрцбург: Кенигсхаузен и Нойманн. ISBN 978-3-8260-4682-7  
  19. ^ Нойманн, Гельмут. 2001. Die Klangreihen-Kompositionslehre nach Othmar Steinbauer (1895–1962) , 184–187, 201–213, 234–236. 2 тома. Франкфурт и др.: Питер Ланг.
  20. ^ Моррис, Роберт (1991). Заметки для занятий по теории атональной музыки , стр. 82. Музыка пика лягушки. ASIN  B0006DHW9I [ISBN не указан].