Строительство силовой установки

Метод создания детерминированных конечных автоматов

В теории вычислений и теории автоматов построение powerset или построение subset является стандартным методом преобразования недетерминированного конечного автомата (NFA) в детерминированный конечный автомат (DFA), который распознает тот же формальный язык . Это важно в теории, поскольку устанавливает, что NFA, несмотря на их дополнительную гибкость, не способны распознавать любой язык, который не может быть распознан некоторыми DFA. Это также важно на практике для преобразования более простых в построении NFA в более эффективно исполняемые DFA. Однако, если NFA имеет n состояний, результирующий DFA может иметь до 2 ⁿ состояний, экспоненциально большее число, что иногда делает построение непрактичным для больших NFA.

Конструкция, иногда называемая конструкцией множества Рабина–Скотта (или конструкцией подмножества), чтобы отличать ее от аналогичных конструкций для других типов автоматов, была впервые опубликована Майклом О. Рабином и Даной Скотт в 1959 году. ^[1]

Интуиция

Чтобы смоделировать работу DFA на заданной входной строке, необходимо отслеживать одно состояние в любой момент времени: состояние, которого достигнет автомат после просмотра префикса ввода. Напротив, чтобы смоделировать NFA, необходимо отслеживать набор состояний: все состояния, которых автомат может достичь после просмотра того же префикса ввода, в соответствии с недетерминированным выбором, сделанным автоматом. Если после определенного префикса ввода может быть достигнут набор S состояний, то после следующего входного символа x набор достижимых состояний является детерминированной функцией S и x . Следовательно, наборы достижимых состояний NFA играют ту же роль в симуляции NFA, что и отдельные состояния DFA в симуляции DFA, и фактически наборы состояний NFA, появляющиеся в этой симуляции, могут быть переинтерпретированы как состояния DFA. ^[2]

Строительство

Конструкция powerset применяется наиболее непосредственно к NFA, который не допускает преобразований состояний без потребления входных символов (т. е. «ε-ходов»). Такой автомат может быть определен как 5-кортеж ( Q , Σ, T , q0 , _F ) , в котором Q — множество состояний, Σ — множество входных символов, _T — функция перехода (отображающая состояние и входной символ в множество состояний), q0 — начальное состояние, а F — множество допускающих состояний. Соответствующий DFA имеет состояния _, соответствующие подмножествам Q. Начальное состояние DFA — это { q0 } , (одноэлементный) набор начальных состояний. Функция перехода DFA отображает состояние S (представляющее подмножество Q ) и входной символ x в множество T ( S , x ) = ∪{ T ( q , x ) | q ∈ S } , множество всех состояний, которые могут быть достигнуты с помощью x -перехода из состояния в S . Состояние S DFA является принимающим состоянием тогда и только тогда, когда по крайней мере один член S является принимающим состоянием NFA. ^{[2] [3]}

В простейшей версии конструкции powerset множество всех состояний DFA является powerset Q , множеством всех возможных подмножеств Q . Однако многие состояния результирующего DFA могут быть бесполезны, поскольку они могут быть недостижимы из начального состояния. Альтернативная версия конструкции создает только состояния, которые фактически достижимы. [ ^4]

NFA с ε-ходами

Для NFA с ε-ходами (также называемого ε-NFA) конструкция должна быть изменена для работы с ними путем вычисления ε- замыкания состояний: множества всех состояний, достижимых из некоторого заданного состояния с использованием только ε-ходов. Ван Норд признает три возможных способа включения этого вычисления замыкания в конструкцию powerset: ^[5]

1. Вычислите ε-замыкание всего автомата в качестве шага предварительной обработки, создав эквивалентный NFA без ε-ходов, затем примените обычную конструкцию powerset. Эта версия, также обсуждаемая Хопкрофтом и Ульманом, ^[6] проста в реализации, но непрактична для автоматов с большим количеством ε-ходов, которые обычно возникают в приложениях обработки естественного языка . ^[5]
2. Во время вычисления powerset вычислите ε-замыкание каждого состояния q , рассматриваемого алгоритмом (и кэшируйте результат). ${\displaystyle \{q'~|~q\to _{\varepsilon }^{*}q'\}}$
3. Во время вычисления множества вычисляется ε-замыкание каждого подмножества состояний Q' , рассматриваемого алгоритмом, и его элементы добавляются к Q' . ${\displaystyle \{q'~|~\exists q\in Q',q\to _{\varepsilon }^{*}q'\}}$

Множественные начальные состояния

Если НКА определены так, чтобы допускать несколько начальных состояний, ^[7] начальное состояние соответствующего ДКА представляет собой множество всех начальных состояний НКА или (если НКА также имеет ε-движения) множество всех состояний, достижимых из начальных состояний с помощью ε-движений.

Пример

Нижеприведенный NFA имеет четыре состояния: состояние 1 является начальным, а состояния 3 и 4 являются принимающими. Его алфавит состоит из двух символов 0 и 1, и он имеет ε-ходы.

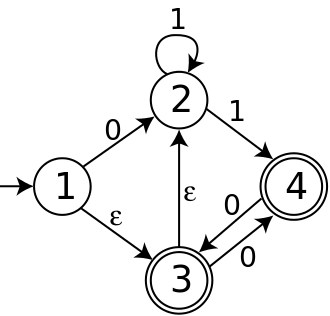
Начальное состояние DFA, построенного из этого NFA, представляет собой множество всех состояний NFA, которые достижимы из состояния 1 с помощью ε-ходов; то есть это множество {1,2,3}. Переход из {1,2,3} с помощью входного символа 0 должен следовать либо по стрелке из состояния 1 в состояние 2, либо по стрелке из состояния 3 в состояние 4. Кроме того, ни состояние 2, ни состояние 4 не имеют исходящих ε-ходов. Следовательно, T ({1,2,3},0) = {2,4}, и по тем же соображениям полный DFA, построенный из NFA, выглядит так, как показано ниже.

Как видно из этого примера, из начального состояния DFA достижимы пять состояний; оставшиеся 11 множеств в powerset множества состояний NFA недостижимы.

Сложность

NFA с 5 состояниями (слева), чей DFA (справа) требует 16 состояний. ^[4]

Поскольку состояния DFA состоят из наборов состояний NFA, NFA с n -состояниями может быть преобразован в DFA с не более чем 2 ⁿ состояниями. ^[2] Для каждого n существуют NFA с n -состояниями, такие, что каждое подмножество состояний достижимо из исходного подмножества, так что преобразованный DFA имеет ровно 2 ⁿ состояний, что дает Θ( 2 ⁿ ) наихудшую временную сложность. ^{[8] [9]} Простым примером, требующим почти такого количества состояний, является язык строк в алфавите {0,1}, в котором есть не менее n символов, n -й от последнего из которых равен 1. Его можно представить с помощью NFA с ( n + 1) состояниями, но для этого требуется 2 ⁿ состояний DFA, по одному для каждого n -символьного суффикса ввода; см. рисунок для n = 4. ^[4 ]

Приложения

Алгоритм Бжозовски для минимизации DFA использует конструкцию powerset дважды. Он преобразует входной DFA в NFA для обратного языка, обращая все его стрелки и меняя роли начальных и принимающих состояний, преобразует NFA обратно в DFA, используя конструкцию powerset, а затем повторяет свой процесс. Его наихудшая сложность является экспоненциальной, в отличие от некоторых других известных алгоритмов минимизации DFA, но во многих примерах он работает быстрее, чем предполагает его наихудшая сложность. ^[10]

Конструкция Сафры, преобразующая недетерминированный автомат Бюхи с n состояниями в детерминированный автомат Мюллера или в детерминированный автомат Рабина с 2 ^{O( n log n )} состояниями, использует конструкцию powerset как часть своего механизма. ^[11]

Ссылки

1. Рабин, MO ; Скотт, Д. (1959). «Конечные автоматы и их проблемы принятия решений». IBM Journal of Research and Development . 3 (2): 114–125. doi :10.1147/rd.32.0114. ISSN  0018-8646.
2. Sipser, Michael (1997). "Теорема 1.19". Введение в теорию вычислений . С. 55–56. ISBN 0-534-94728-X.
3. Хопкрофт, Джон Э .; Ульман, Джеффри Д. (1979). «Эквивалентность DFA и NFA». Введение в теорию автоматов, языки и вычисления . Reading Massachusetts: Addison-Wesley. стр. 22–23. ISBN 0-201-02988-X.
4. Шнайдер, Клаус (2004). Проверка реактивных систем: формальные методы и алгоритмы. Springer. С. 210–212. ISBN 978-3-540-00296-3.
5. Van Noord, Gertjan (2000). «Обработка движений эпсилон при построении подмножеств». Computational Linguistics . 26 (1): 61–76. arXiv : cmp-lg/9804003 . doi : 10.1162/089120100561638. S2CID  5622079.
6. Хопкрофт и Ульман (1979), стр. 26–27.
7. Роте, Йорг (2006). Теория сложности и криптология: Введение в криптокомплексность. Тексты по теоретической информатике. Springer. С. 21–22. ISBN 9783540285205..
8. Лупанов, Олег Б. (1963). «Сравнение двух типов конечных источников». Проблемы кибернетики . 9 : 321–326.
9. Мур, Фрэнк Р. (1971). «О границах размера множества состояний в доказательствах эквивалентности детерминированных, недетерминированных и двусторонних конечных автоматов». IEEE Transactions on Computers . C-20 (10): 1211–1214. doi :10.1109/TC.1971.223108. S2CID  206618275..
10. Brzozowski, JA (1963). «Канонические регулярные выражения и минимальные графы состояний для определенных событий». Proc. Sympos. Math. Theory of Automata (Нью-Йорк, 1962) . Polytechnic Press of Polytechnic Inst. of Brooklyn, Brooklyn, NY, стр. 529–561. MR  0175719.
11. Сафра, С. (1988). «О сложности ω-автоматов». Труды 29-го ежегодного симпозиума по основам компьютерной науки (FOCS '88) . Вашингтон, округ Колумбия, США: IEEE Computer Society. стр. 319–327. doi :10.1109/SFCS.1988.21948..

Дальнейшее чтение

• Андерсон, Джеймс Эндрю (2006). Теория автоматов с современными приложениями. Cambridge University Press. С. 43–49. ISBN 978-0-521-84887-9.