Ламбертовское отражение

Диаграмма диффузного отражения Ламберта. Черная стрелка показывает падающее излучение , а красные стрелки показывают отраженную интенсивность излучения в каждом направлении. При просмотре с разных углов отраженная интенсивность излучения и видимая площадь поверхности изменяются в зависимости от косинуса угла обзора, поэтому отраженное излучение (интенсивность на единицу площади) одинаково для всех углов обзора.

Ламбертовское отражение — это свойство, которое определяет идеальную «матовую» или диффузно отражающую поверхность. Видимая яркость ламбертовской поверхности для наблюдателя одинакова независимо от угла зрения наблюдателя. ^[1] Точнее, отраженная интенсивность излучения подчиняется закону косинуса Ламберта , который делает отраженное излучение одинаковым во всех направлениях. Ламбертовское отражение названо в честь Иоганна Генриха Ламберта , который ввел концепцию идеальной диффузии в своей книге 1760 года «Фотометрия» .

Примеры

Необработанная древесина демонстрирует приблизительно ламбертовское отражение, но древесина, отделанная глянцевым слоем полиуретана, не имеет, поскольку глянцевое покрытие создает зеркальные блики . Хотя не все грубые поверхности являются ламбертовскими, это часто является хорошим приближением и часто используется, когда характеристики поверхности неизвестны. ^[2]

Спектралон — это материал, разработанный для демонстрации почти идеального ламбертовского отражения. ^[1]

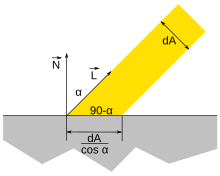
Использование в компьютерной графике

В компьютерной графике ламбертовское отражение часто используется в качестве модели для диффузного отражения . Этот метод заставляет все замкнутые многоугольники (например, треугольник в трехмерной сетке) отражать свет одинаково во всех направлениях при визуализации. Однако отражение уменьшается, когда поверхность наклонена от перпендикулярности к источнику света, поскольку область освещается меньшей долей падающего излучения. ^[3]

Отражение вычисляется путем взятия скалярного произведения единичного вектора нормали поверхности , , и нормализованного вектора направления света , направленного от поверхности к источнику света. Затем это число умножается на цвет поверхности и интенсивность света, падающего на поверхность: $\mathbf {N}$ $\mathbf {L}$

B_{D}=\mathbf {L} \cdot \mathbf {N} CI_{\text{L}}

где - яркость диффузно отраженного света, - цвет, - интенсивность входящего света. Потому что $B_{D}$ $C$ $I_{\text{L}}$

\mathbf {L} \cdot \mathbf {N} =|N||L|\cos {\alpha }=\cos {\alpha }

где — угол между направлениями двух векторов, яркость будет максимальной, если поверхность перпендикулярна вектору света, и минимальной, если вектор света пересекает поверхность под углом скольжения. $\alpha$

Ламбертовское отражение от полированных поверхностей обычно сопровождается зеркальным отражением ( блеском ), при котором яркость поверхности максимальна, когда наблюдатель находится в идеальном направлении отражения (т. е. где направление отраженного света является отражением направления падающего света на поверхность), и резко падает.

Другие волны

Хотя ламбертовское отражение обычно относится к отражению света объектом, его можно использовать для обозначения отражения любой волны. Например, в ультразвуковой визуализации говорят, что «грубые» ткани демонстрируют ламбертовское отражение. ^[4]

Смотрите также

Ссылки

^ ab Ikeuchi, Katsushi (2014). «Отражение Ламберта». Энциклопедия компьютерного зрения . Springer. стр. 441–443. doi :10.1007/978-0-387-31439-6_534. ISBN 978-0-387-30771-8. S2CID 11390799.
^ Лу, Ренфу (2016). Технология рассеяния света для оценки свойств, качества и безопасности пищевых продуктов. CRC Press . стр. 26. ISBN 9781482263350.
^ Энджел, Эдвард (2003). Интерактивная компьютерная графика: подход сверху вниз с использованием OpenGL (третье изд.). Addison-Wesley . ISBN 978-0-321-31252-5.
^ Килан, Роберт; Шимада, Кенджи; Рабин, Йоед (2016-06-23). «Моделирование артефактов ультразвуковой визуализации на основе графического процессора для обучения криохирургии». Технологии в исследованиях и лечении рака . 16 (1): 5–14. doi :10.1177/1533034615623062. ISSN 1533-0346. PMC 5616109. PMID 26818026 .