Повторная выборка Ланцоша

Частичный график дискретного сигнала (черные точки) и его интерполяции Ланцоша (сплошная синяя кривая) с параметром размера a, равным 1 (вверху), 2 (в середине) и 3 (внизу). Также показаны две копии ядра Ланцоша, смещенные и масштабированные, соответствующие образцам 4 и 11 (пунктирные кривые).

Фильтрация Ланцоша и повторная выборка Ланцоша — это два применения определенной математической формулы. Она может использоваться как фильтр нижних частот или использоваться для плавной интерполяции значения цифрового сигнала между его выборками . В последнем случае она отображает каждую выборку заданного сигнала в переведенную и масштабированную копию ядра Ланцоша , которое является функцией sinc, оконной центральным лепестком второй, более длинной функции sinc. Затем сумма этих переведенных и масштабированных ядер оценивается в желаемых точках.

Повторная выборка Ланцоша обычно используется для увеличения частоты дискретизации цифрового сигнала или для ее смещения на долю интервала дискретизации. Она также часто используется для многомерной интерполяции , например, для изменения размера или поворота цифрового изображения . Она считается «лучшим компромиссом» среди нескольких простых фильтров для этой цели. ^[1]

Фильтр был изобретен Клодом Дюшоном, который назвал его в честь Корнелиуса Ланцоша из-за использования Дюшоном сигма-аппроксимации при построении фильтра, метода, созданного Ланцошем. ^[2]

Определение

ядро Ланцоша

Ядра Ланцоша для случаев a = 1, 2 и 3 с их частотными спектрами. Фильтр sinc имел бы срез на частоте 0,5.

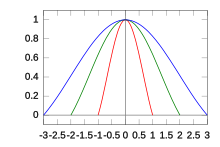
Влияние каждого входного образца на интерполированные значения определяется ядром реконструкции фильтра $L (x)$ , называемым ядром Ланцоша. Это нормализованная функция sinc $sinc(x)$ , умноженная на окно Ланцоша ,или sinc-окно , которое является центральным лепестком горизонтально растянутой sinc-функции $sinc(x / a)$ для $- a \leq x \leq a$ .

L(x)={\begin{cases}\operatorname {sinc} (x)\operatorname {sinc} (x/a)&{\text{если}}\ -a<x<a,\\0&{\text{иначе}}.\end{cases}}

Эквивалентно,

L(x)={\begin{cases}1&{\text{if}}\ x=0,\\{\dfrac {a\sin(\pi x)\sin(\pi x/a)}{\pi ^{2}x^{2}}}&{\text{if}}\ -a\leq x<a\ {\text{and}}\ x\neq 0,\\0&{\text{individually}}.\end{cases}}

Параметр $a$ — это положительное целое число, обычно 2 или 3, которое определяет размер ядра. Ядро Ланцоша имеет $2 a - 1$ лепестков: положительный в центре и $a - 1$ чередующихся отрицательных и положительных лепестков с каждой стороны.

Формула интерполяции

При наличии одномерного сигнала с выборками $s i$ для целых значений $i$ значение $S (x),$ интерполированное при произвольном действительном аргументе $x,$ получается путем дискретной свертки этих выборок с ядром Ланцоша: ^[3]

S(x)=\sum _{i=\lfloor x\rfloor -a+1}^{\lfloor x\rfloor +a}s_{i}L(xi),

где $a$ — параметр размера фильтра, а — функция пола . Границы этой суммы таковы, что ядро равно нулю вне их. $\lfloor x\rfloor$

Характеристики

Пока параметр $a$ является положительным целым числом, ядро Ланцоша непрерывно всюду, а его производная определена и непрерывна всюду (даже при $x = \pm a$ , где обе функции sinc стремятся к нулю). Следовательно, восстановленный сигнал $S (x)$ также будет непрерывным, с непрерывной производной.

Ядро Ланцоша равно нулю при каждом целочисленном аргументе $x$ , за исключением $x = 0$ , где оно имеет значение 1. Следовательно, восстановленный сигнал точно интерполирует заданные выборки: мы будем иметь $S (x) = s i$ для каждого целочисленного аргумента $x = i$ .

Повторная выборка Ланцоша — это одна из форм общего метода, разработанного Ланцошем для противодействия явлению Гиббса путем умножения коэффициентов усеченного ряда Фурье на , где — индекс коэффициента, а — количество сохраняемых коэффициентов. ^[4] Те же рассуждения применимы и в случае усеченных функций, если мы хотим удалить колебания Гиббса в их спектре. $\mathrm {sinc} (\pi k/m)$ $к$ $м$

Многомерная интерполяция

Ядро фильтра Ланцоша в двух измерениях:

L(x,y)=L(x)L(y).

Оценка

Преимущества

Теоретически оптимальным фильтром реконструкции для сигналов с ограниченной полосой пропускания является sinc-фильтр , который имеет бесконечную поддержку . Фильтр Ланцоша является одним из многих практических (конечно поддерживаемых) приближений sinc-фильтра. Каждое интерполированное значение является взвешенной суммой $2 a$ последовательных входных выборок. Таким образом, изменяя параметр $2 a,$ можно пожертвовать скоростью вычислений ради улучшения частотной характеристики. Параметр также позволяет выбирать между более плавной интерполяцией или сохранением резких переходных процессов в данных. Для обработки изображений компромисс заключается между уменьшением артефактов наложения спектров и сохранением резких краев. Также, как и при любой такой обработке, нет никаких результатов для границ изображения. Увеличение длины ядра увеличивает обрезку краев изображения.

Фильтр Ланцоша сравнивался с другими методами интерполяции для дискретных сигналов, в частности с другими оконными версиями фильтра sinc. Турковски и Габриэль утверждали, что фильтр Ланцоша (с $a = 2$ ) является «лучшим компромиссом с точки зрения уменьшения наложения спектров, резкости и минимального звона» по сравнению с усеченным sinc и оконным sinc Бартлетта , косинусным и Ханна для прореживания и интерполяции двумерных данных изображения. ^[1] По словам Джима Блинна , ядро Ланцоша (с $a = 3$ ) «сохраняет низкие частоты и отклоняет высокие частоты лучше, чем любой (достижимый) фильтр, который мы видели до сих пор». ^[5]

Интерполяция Ланцоша — популярный фильтр для «масштабирования» видео в различных медиа-утилитах, таких как AviSynth ^[6] и FFmpeg ^[7] .

Ограничения

Поскольку ядро предполагает отрицательные значения для $a > 1$ , интерполированный сигнал может быть отрицательным, даже если все выборки положительны. В более общем смысле диапазон значений интерполированного сигнала может быть шире, чем диапазон, охватываемый дискретными значениями выборки. В частности, могут быть артефакты звона непосредственно перед и после резких изменений в значениях выборки, что может привести к артефактам отсечения . Однако эти эффекты уменьшены по сравнению с (не оконным) фильтром sinc. Для a = 2 (трехлепестковое ядро) звон составляет < 1%.

При использовании фильтра Ланцоша для повторной выборки изображения эффект звона создаст светлые и темные ореолы вдоль любых резких краев. Хотя эти полосы могут быть визуально раздражающими, они помогают увеличить воспринимаемую резкость и, следовательно, обеспечивают форму улучшения краев . Это может улучшить субъективное качество изображения, учитывая особую роль резкости краев в зрении . ^[8]

В некоторых приложениях артефакты отсечения нижнего уровня можно устранить, преобразовав данные в логарифмическую область перед фильтрацией. В этом случае интерполированные значения будут представлять собой взвешенное геометрическое среднее, а не арифметическое среднее входных выборок.

Ядро Ланцоша не обладает свойством разбиения единицы . То есть сумма всех целочисленно транслированных копий ядра не всегда равна 1. Поэтому интерполяция Ланцоша дискретного сигнала с постоянными выборками не дает постоянной функции. Этот дефект наиболее очевиден, когда $a$ $= 1.$ Кроме того, при $a$ $= 1$ интерполированный сигнал имеет нулевую производную при каждом целочисленном аргументе. Это довольно академично, поскольку использование однолепесткового ядра ( a = 1) теряет все преимущества подхода Ланцоша и обеспечивает плохой фильтр. Существует много лучших однолепестковых колоколообразных оконных функций. ${\ textstyle U (x) = \ sum _ {i \ in \ mathbb {Z} } L (xi)}$

Разбиение единицы можно ввести с помощью нормализации,

L'(xi)={\frac {L(xi)}{\sum _{j=1-a}^{a}L(xj)}}

для . $0\leq x<1$

Смотрите также

Ссылки

^ ab Turkowski, Ken; Gabriel, Steve (1990). «Фильтры для общих задач повторной выборки». В Glassner, Andrew S. (ред.). Graphics Gems I . Academic Press. стр. 147–165. CiteSeerX 10.1.1.116.7898 . ISBN 978-0-12-286165-9.
^ Клод, Дюшон (1979-08-01). «Фильтрация Ланцоша в одном и двух измерениях». Журнал прикладной метеорологии . 18 (8): 1016–1022. Bibcode :1979JApMe..18.1016D. doi : 10.1175/1520-0450(1979)018<1016:LFIOAT>2.0.CO;2 .
^ Бургер, Вильгельм; Бердж, Марк Дж. (2009). Принципы цифровой обработки изображений: основные алгоритмы. Springer. С. 231–232. ISBN 978-1-84800-194-7.
^ Ланцос, Корнелиус (1988). Прикладной анализ. Нью-Йорк: Dover Publications. С. 219–221. ISBN 0-486-65656-X. OCLC 17650089.
^ Блинн, Джим (1998). Уголок Джима Блинна: грязные пиксели. Морган Кауфманн. стр. 26–27. ISBN 978-1-55860-455-1.
^ "Изменить размер". Avisynth. 2015-01-01 . Получено 2015-07-27 .
^ "Руководство: Преобразование видео с помощью FFDShow - Форумы Neowin". Neowin.net. 2006-04-18 . Получено 2012-07-31 .
^ "IPOL: Линейные методы интерполяции изображений". Ipol.im. 2011-09-27 . Получено 2012-07-31 .

Внешние ссылки

Примеры геометрии антизернистости: image_filters.cppдемонстрирует сравнение многократной передискретизации изображения с различными ядрами.
imageresampler: общедоступный класс передискретизации изображений на языке C++ с поддержкой нескольких оконных ядер фильтра Ланцоша.