В телекоммуникациях линейный код — это шаблон напряжения, тока или фотонов, используемый для представления цифровых данных , передаваемых по каналу связи или записываемых на носитель . Этот набор сигналов обычно называется ограниченным кодом в системах хранения данных. [1] Некоторые сигналы более подвержены ошибкам, чем другие, поскольку физика канала связи или носителя ограничивает набор сигналов, которые можно надежно использовать. [2]
Распространенными линейными кодировками являются униполярная , полярная , биполярная и манчестерский код .
После линейного кодирования сигнал передается через физический канал связи, либо через среду передачи , либо через среду хранения данных . [3] [4] Наиболее распространенными физическими каналами являются:
Некоторые из наиболее распространенных двоичных линейных кодов включают в себя:
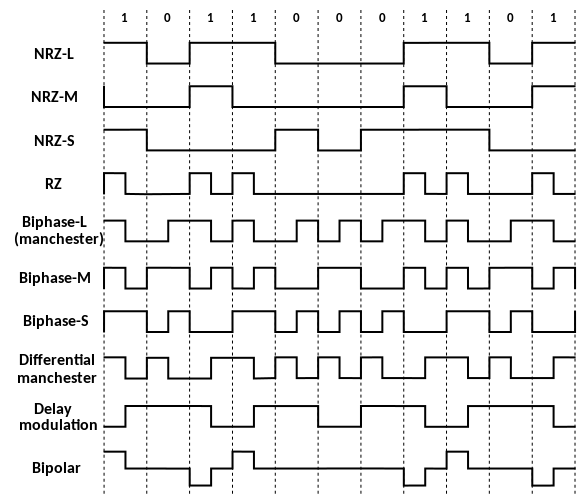
Каждый линейный код имеет свои преимущества и недостатки. Линейные коды выбираются с учетом одного или нескольких из следующих критериев:
Большинство каналов связи на большие расстояния не могут надежно передавать компонент постоянного тока . Компонент постоянного тока также называется диспаратностью , смещением или коэффициентом постоянного тока . Диспаратность битовой комбинации — это разница в количестве единичных битов по сравнению с количеством нулевых битов. Текущая диспаратность — это текущая сумма диспаратности всех ранее переданных битов. [5] Самый простой возможный линейный код, униполярный , дает слишком много ошибок в таких системах, поскольку имеет неограниченную компоненту постоянного тока.
Большинство линейных кодов устраняют компонент DC – такие коды называются DC-balanced , zero-DC или DC-free. Существует три способа устранения компонента DC:
Биполярные линейные коды имеют две полярности, обычно реализуются как RZ и имеют основание три, поскольку существуют три различных выходных уровня (отрицательный, положительный и нулевой). Одним из принципиальных преимуществ этого типа кода является то, что он может устранить любую постоянную составляющую. Это важно, если сигнал должен проходить через трансформатор или длинную линию передачи.
К сожалению, несколько каналов дальней связи имеют неоднозначность полярности. В этих каналах компенсируют нечувствительные к полярности линейные коды. [6] [7] [8] [9] Существует три способа обеспечения однозначного приема битов 0 и 1 по таким каналам:
Для надежного восстановления часов на приемнике ограничение длины запуска может быть наложено на сгенерированную канальную последовательность, т. е. максимальное количество последовательных единиц или нулей ограничено разумным числом. Период часов восстанавливается путем наблюдения за переходами в полученной последовательности, так что максимальная длина запуска гарантирует достаточное количество переходов для обеспечения качества восстановления часов.
Коды RLL определяются четырьмя основными параметрами: m , n , d , k . Первые два, m / n , относятся к скорости кода, а оставшиеся два определяют минимальное d и максимальное k количество нулей между последовательными единицами. Это используется как в телекоммуникациях , так и в системах хранения, которые перемещают носитель мимо фиксированной записывающей головки . [10]
В частности, RLL ограничивает длину отрезков (прогонов) повторяющихся битов, в течение которых сигнал не изменяется. Если прогоны слишком длинные, восстановление тактовой частоты затруднено; если они слишком короткие, высокие частоты могут быть ослаблены каналом связи. Модулируя данные , RLL снижает временную неопределенность при декодировании сохраненных данных, что может привести к возможной ошибочной вставке или удалению битов при обратном считывании данных. Этот механизм гарантирует, что границы между битами всегда могут быть точно найдены (предотвращая проскальзывание битов ), при этом эффективно используя носитель для надежного хранения максимального объема данных в заданном пространстве.
Ранние дисководы использовали очень простые схемы кодирования, такие как код RLL (0,1) FM, за которым следовал код RLL (1,3) MFM, которые широко использовались в жестких дисках до середины 1980-х годов и до сих пор используются в цифровых оптических дисках, таких как CD , DVD , MD , Hi-MD и Blu-ray, с использованием кодов EFM и EFMPLus. [11] Более плотные коды RLL (2,7) и RLL (1,7) стали фактическими стандартами для жестких дисков к началу 1990-х годов. [ необходима цитата ]
Линейное кодирование должно позволить приемнику синхронизироваться с фазой принимаемого сигнала. Если восстановление тактовой частоты не идеально, то декодируемый сигнал не будет оцифрован в оптимальные моменты времени. Это увеличит вероятность ошибок в принимаемых данных.
Бифазные линейные коды требуют по крайней мере одного перехода за битовое время. Это облегчает синхронизацию трансиверов и обнаружение ошибок, однако скорость передачи данных выше, чем у кодов NRZ.
Линейный код обычно отражает технические требования к среде передачи, например, оптоволокну или экранированной витой паре . Эти требования уникальны для каждой среды, поскольку каждая из них имеет разное поведение, связанное с помехами, искажениями, емкостью и затуханием. [12]
Линейные коды ... облегчают передачу данных по телекоммуникационным и компьютерным сетям и их хранение в мультимедийных системах.
При использовании модуляции данных PSK существует потенциальная возможность неоднозначности полярности принимаемых символов канала. Эту проблему можно решить одним из двух способов. Во-первых ... так называемый прозрачный код. ...
Еще одним преимуществом дифференциального кодирования является его нечувствительность к полярности сигнала. ... Если выводы витой пары случайно перепутаны...
Дано подробное описание предельных свойств runlength-limited sequences.
Описана высокоплотная альтернатива EFM.
В этой статье использованы материалы из общедоступного федерального стандарта 1037C. Администрация общих служб . Архивировано из оригинала 2022-01-22. (в поддержку MIL-STD-188 ).