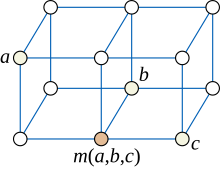
В теории графов , разделе математики , медианный граф — это неориентированный граф , в котором каждые три вершины a , b и c имеют уникальную медиану : вершину m ( a , b , c ), которая принадлежит кратчайшим путям между каждой парой. из a , b и c .
Концепция медианных графов уже давно изучается, например, Биркгофом и Киссом (1947) или (более подробно) Аванном (1961), но первой статьей, в которой они были названы «медианными графами», по-видимому, была Небески (1971). Как пишут Чанг , Грэм и Сакс, «медианные графы естественным образом возникают при изучении упорядоченных множеств и дискретных дистрибутивных решеток и имеют обширную литературу». [1] В филогенетике граф Бунемана, представляющий все эволюционные деревья максимальной экономии, является медианным графом. [2] Медианные графики также возникают в теории социального выбора : если набор альтернатив имеет структуру медианного графа, можно однозначно определить предпочтение большинства среди них. [3]
Дополнительные обзоры медианных графиков даны Клавжаром и Малдером (1999), Бандельтом и Чепоем (2008) и Кнутом (2008).
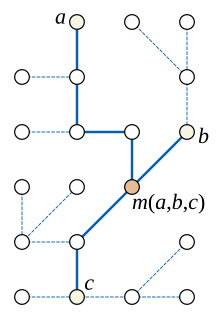
Каждое дерево представляет собой медианный граф. Чтобы убедиться в этом, заметим, что в дереве объединение трех кратчайших путей между парами трех вершин a , b и c само по себе является путем или поддеревом, образованным тремя путями, встречающимися в одном центральном узле со степенью три. Если объединение трех путей само по себе является путем, медиана m ( a , b , c ) равна одной из a , b или c , в зависимости от того, какая из этих трех вершин находится между двумя другими на пути. Если поддерево, образованное объединением трех путей, не является путем, медиана трех вершин является центральным узлом поддерева третьей степени. [4]
Дополнительные примеры медианных графиков представлены сеточными графиками . В сеточном графике координаты медианы m ( a , b , c ) можно найти как медиану координат a , b и c . И наоборот, оказывается, что в каждом медианном графе можно пометить вершины точками целочисленной решетки таким образом, что таким образом можно вычислить медианы по координатам. [5]
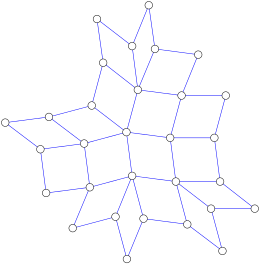
Квадратные графы , плоские графы, в которых все внутренние грани являются четырехугольниками, а все внутренние вершины имеют четыре или более инцидентных ребра, являются еще одним подклассом медианных графов. [6] Полимино является частным случаем квадратного графа и, следовательно, также образует медианный граф . [7]
Симплекс -граф κ( G ) произвольного неориентированного графа G имеет вершину для каждой клики (полного подграфа) графа G ; две вершины κ( G ) соединены ребром, если соответствующие клики отличаются на одну вершину из G . Симплексный граф всегда является медианным графом, в котором медиана данной тройки клик может быть сформирована с использованием правила большинства для определения того, какие вершины клик включить. [8]
Ни один граф циклов длины, отличной от четырех, не может быть медианным графом. Каждый такой цикл имеет три вершины a , b и c, так что три кратчайших пути полностью огибают цикл, не имея общего пересечения. Для такой тройки вершин не может быть медианы.
В произвольном графе для каждых двух вершин a и b минимальное количество ребер между ними называется их расстоянием и обозначается d ( x , y ). Интервал вершин, лежащих на кратчайших путях между a и b , определяется как
Медианный граф определяется тем свойством, что для каждых трех вершин a , b и c эти интервалы пересекаются в одной точке:
Эквивалентно, для каждых трех вершин a , b и c можно найти вершину m ( a , b , c ) такую, что невзвешенные расстояния в графе удовлетворяют равенствам
и m ( a , b , c ) — единственная вершина, для которой это верно.
Также возможно определить медианные графы как множества решений задач 2-выполнимости , как ретракты гиперкубов , как графики конечных медианных алгебр , как графы Бунемана расщепляемых систем Хелли и как графики Windex 2; см. разделы ниже.

В теории решеток граф конечной решетки имеет вершину для каждого элемента решетки и ребро для каждой пары элементов в отношении накрытия решетки. Решетки обычно представляются визуально с помощью диаграмм Хассе , которые представляют собой рисунки графов решеток. Эти графы, особенно в случае дистрибутивных решеток , оказываются тесно связанными с медианными графами.
В дистрибутивной решетке самодвойственная троичная медианная операция Биркгофа [9]
удовлетворяет определенным ключевым аксиомам, которые он разделяет с обычной медианой чисел в диапазоне от 0 до 1 и с медианными алгебрами в более общем плане:
Распределительный закон может быть заменен ассоциативным законом: [10]
Медианную операцию также можно использовать для определения понятия интервалов для дистрибутивных решеток:
Граф конечной дистрибутивной решетки имеет ребро между вершинами a и b всякий раз, когда I ( a , b ) = { a , b }. Для каждых двух вершин a и b этого графа интервал I ( a , b ) , определенный выше в терминах теории решетки, состоит из вершин на кратчайших путях от a до b и, таким образом, совпадает с интервалами теории графов, определенными ранее. Для каждых трех элементов решетки a , b и c m ( a , b , c ) является уникальным пересечением трех интервалов I ( a , b ) , I ( a , c ) и I ( b , c ) . [12] Следовательно, граф произвольной конечной дистрибутивной решетки является медианным графом. И наоборот, если медианный граф G содержит две вершины 0 и 1 такие, что каждая другая вершина лежит на кратчайшем пути между ними (эквивалентно, m (0, a , 1) = a для всех a ), то мы можем определить дистрибутив решетка, в которой a ∧ b = m ( a ,0, b ) и a ∨ b = m ( a ,1, b ), а G будет графиком этой решетки. [13]
Даффус и Ривал (1983) характеризуют графы дистрибутивных решеток непосредственно как сохраняющие диаметр ретракты гиперкубов. В более общем смысле, каждый медианный граф порождает троичную операцию m, удовлетворяющую идемпотентности, коммутативности и дистрибутивности, но, возможно, без единичных элементов дистрибутивной решетки. Любая тернарная операция на конечном множестве, удовлетворяющая этим трем свойствам (но не обязательно имеющая 0 и 1 элемент), аналогичным образом приводит к медианному графу. [14]
В медианном графе набор вершин S называется выпуклым, если для каждых двух вершин a и b , принадлежащих S , весь интервал I ( a , b ) является подмножеством S. Эквивалентно, учитывая два определения интервалов, приведенные выше, S является выпуклой, если она содержит каждый кратчайший путь между двумя своими вершинами или если она содержит медиану каждого набора из трех точек, по крайней мере две из которых принадлежат S . Заметим, что пересечение каждой пары выпуклых множеств само по себе является выпуклым. [15]
Выпуклые множества в медианном графе обладают свойством Хелли : если F — произвольное семейство попарно пересекающихся выпуклых множеств, то все множества в F имеют общее пересечение. [16] Ибо, если F имеет в себе только три выпуклых множества S , T и U , причем a находится в пересечении пары S и T , b в пересечении пары T и U и c в пересечении пары S и T, b в пересечении пары T и U и c в пересечении пары S и T, пары S и U , то каждый кратчайший путь от a до b должен лежать внутри T по выпуклости, и аналогично каждый кратчайший путь между двумя другими парами вершин должен лежать внутри двух других наборов; но m ( a , b , c ) принадлежит путям между всеми тремя парами вершин, поэтому оно лежит внутри всех трех наборов и образует часть их общего пересечения. Если F содержит более трех выпуклых множеств, результат следует индукцией по числу множеств, поскольку можно заменить произвольную пару множеств в F их пересечением, используя результат для троек множеств, чтобы показать, что замененное семейство все еще попарно пересекается.
Особенно важным семейством выпуклых множеств в медианном графе, играющим роль, аналогичную роли полупространств в евклидовом пространстве, являются множества
определено для каждого ребра uv графа. Другими словами, Wuv состоит из вершин, находящихся ближе к u , чем к v , или, что то же самое, из вершин w , таких, что некоторый кратчайший путь от v до w проходит через u . Чтобы показать, что W uv выпукла, пусть w 1 w 2 ... w k — произвольная кратчайшая, которая начинается и заканчивается внутри W uv ; тогда w 2 также должна лежать внутри W uv , иначе две точки m 1 = m ( u , w 1 , w k ) и m 2 = m ( m 1 , w 2 ... w k ) можно было бы показать (по формуле считая возможные расстояния между вершинами) разными медианами u , w1 и wk , что противоречит определению медианного графа, которое требует, чтобы медианы были уникальными . Таким образом, каждая последующая вершина кратчайшего пути между двумя вершинами Wuv также лежит внутри Wuv , поэтому Wuv содержит все кратчайшие пути между своими узлами , что является одним из определений выпуклости .
Свойство Хелли для множеств W uv играет ключевую роль в описании медианных графов как решения случаев 2-выполнимости (см. ниже).
Медианные графы тесно связаны с множествами решений задач 2-выполнимости , которые можно использовать как для характеристики этих графов, так и для их связи с сохраняющими смежность отображениями гиперкубов. [17]
Экземпляр 2-выполнимости состоит из набора логических переменных и набора предложений — ограничений на определенные пары переменных, требующих, чтобы эти две переменные избегали определенных комбинаций значений. Обычно такие задачи выражаются в конъюнктивной нормальной форме , в которой каждое предложение выражается как дизъюнкция , а весь набор ограничений выражается как конъюнкция предложений, например:
Решением такого случая является присвоение значений истинности переменным, которое удовлетворяет всем условиям или, что то же самое, приводит к тому, что выражение конъюнктивной нормальной формы для экземпляра становится истинным, когда в него подставляются значения переменных. Семейство всех решений имеет естественную структуру в виде медианной алгебры, где медиана трех решений формируется путем выбора каждого значения истинности в качестве мажоритарной функции значений в трех решениях; несложно проверить, что это медианное решение не может нарушить ни одно из условий. Таким образом, эти решения образуют медианный граф, в котором сосед каждого решения формируется путем отрицания набора переменных, все из которых ограничены равными или неравными друг другу.
И наоборот, каждый медианный граф G может быть представлен таким образом как набор решений для экземпляра 2-выполнимости. Чтобы найти такое представление, создайте экземпляр 2-выполнимости, в котором каждая переменная описывает ориентацию одного из ребер в графе (присвоение направления ребру, заставляющее граф становиться направленным , а не ненаправленным), и каждое ограничение позволяет два ребра имеют общую пару ориентаций только тогда, когда существует вершина v такая, что обе ориентации лежат вдоль кратчайших путей от других вершин до v . Каждая вершина v графа G соответствует решению этого случая 2-выполнимости, в котором все ребра направлены в сторону v . Таким образом , каждое решение экземпляра должно исходить из некоторой вершины v , где v — общее пересечение множеств W uw для ребер, направленных от w к u ; это общее пересечение существует благодаря свойству Хелли множеств W uw . Следовательно, решения этого случая 2-выполнимости взаимно однозначно соответствуют вершинам G .
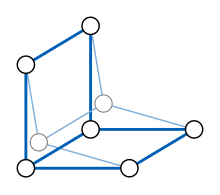
Ретракция графа G — это отображение G с сохранением смежности в один из его подграфов. [18] Точнее, это гомоморфизм графа φ из G в себя такой, что φ( v ) = v для каждой вершины v в подграфе φ(G). Образ ретракции называется ретрактом G. Ретракция является примером метрических отображений : расстояние между φ( v ) и φ( w ) для каждого v и w не более чем равно расстоянию между v и w и равно всякий раз, когда v и w оба принадлежат φ( Г ). Следовательно, ретракт должен быть изометрическим подграфом G : расстояния в ретракте равны расстояниям в G.
Если G — медианный граф, а a , b и c — произвольные три вершины ретракта φ( G ), то φ( m ( a , b , c )) должна быть медианой a , b и c. , и поэтому должно равняться m ( a , b , c ). Следовательно, φ( G ) содержит медианы всех троек своих вершин и также должен быть медианным графом. Другими словами, семейство медианных графов замкнуто относительно операции ретракции. [19]
Граф гиперкуба , в котором вершины соответствуют всем возможным k -битным битвекторам и в котором две вершины смежны, когда соответствующие битовые векторы отличаются только на один бит, является частным случаем k -мерного сеточного графа и, следовательно, является медианным график. Медиану трех битовых векторов a , b и c можно вычислить путем вычисления в каждой позиции бита мажоритарной функции битов a , b и c . Поскольку медианные графы замкнуты при ретракции и включают в себя гиперкубы, каждый ретракт гиперкуба является медианным графом.
И наоборот, каждый медианный граф должен быть ретрактом гиперкуба. [20] Это видно из описанной выше связи между медианными графами и 2-выполнимостью: пусть G — граф решений случая 2-выполнимости; без ограничения общности этот пример можно сформулировать таким образом, что никакие две переменные не всегда равны или не всегда неравны в каждом решении. Тогда пространство всех истинностных присвоений переменным этого экземпляра образует гиперкуб. Для каждого предложения, образованного как дизъюнкция двух переменных или их дополнений, в случае 2-выполнимости можно сформировать ретракцию гиперкуба, в котором истинностные присвоения, нарушающие это предложение, отображаются в истинностные присвоения, в которых обе переменные удовлетворяют этому предложению. без изменения других переменных в истинностном назначении. Композиция сформированных таким образом ретракций для каждого из предложений дает ретракцию гиперкуба на пространство решений экземпляра и, следовательно, дает представление G как ретракта гиперкуба. В частности, медианные графы представляют собой изометрические подграфы гиперкубов и, следовательно, являются частичными кубами . Однако не все частичные кубы являются медианными графами; например, граф циклов с шестью вершинами является частичным кубом, но не является медианным графом.
Как описывают Имрих и Клавжар (2000), изометрическое вложение медианного графа в гиперкуб может быть построено за время O( m log n ), где n и m — количество вершин и ребер графа соответственно. [21]
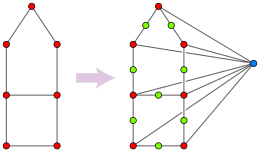
Проблемы проверки того, является ли граф медианным графом и является ли граф свободным от треугольников , были хорошо изучены, когда Имрих, Клавжар и Малдер (1999) заметили, что в некотором смысле они вычислительно эквивалентны. [22] Таким образом, наиболее известная временная граница для проверки того, является ли граф свободным от треугольников, O( m 1,41 ), [23] применима также к проверке того, является ли граф медианным графом, и к любому усовершенствованию алгоритмов тестирования медианного графа. также приведет к улучшению алгоритмов обнаружения треугольников на графиках.
Предположим, что в одном направлении в качестве входных данных задан граф G , и он должен проверить, не содержит ли G треугольников. Из G постройте новый граф H , имеющий в качестве вершин каждое множество из нуля, одной или двух смежных вершин G . Два таких множества считаются смежными в H , если они отличаются ровно на одну вершину. Эквивалентное описание H состоит в том, что оно формируется путем разделения каждого ребра G на путь из двух ребер и добавления новой вершины, соединенной со всеми исходными вершинами G . Этот граф H по построению является частичным кубом, но он является медианным графом только тогда, когда G не содержит треугольников: если a , b и c образуют треугольник в G , то { a , b }, { a , c }, и { b , c } не имеют медианы в H , поскольку такая медиана должна была бы соответствовать множеству { a , b , c }, но наборы из трех или более вершин G не образуют вершины в H . Следовательно, G свободен от треугольников тогда и только тогда, когда H — медианный граф. В случае, когда G не содержит треугольников, H является его симплекс-графом . Алгоритм для эффективной проверки того, является ли H медианным графом, с помощью этой конструкции также может использоваться для проверки того, является ли G свободным от треугольников. Это преобразование сохраняет вычислительную сложность задачи, поскольку размер H пропорционален размеру G.
Сокращение в другом направлении, от обнаружения треугольников к тестированию медианного графа, является более сложным и зависит от предыдущего алгоритма распознавания медианного графа Хагауэра, Имриха и Клавжара (1999), который проверяет несколько необходимых условий для медианных графов за почти линейное время. . Ключевой новый шаг включает в себя использование поиска в ширину для разделения вершин графа на уровни в соответствии с их расстояниями от некоторой произвольно выбранной корневой вершины, формирование графа из каждого уровня, в котором две вершины являются смежными, если они имеют общего соседа на предыдущем уровне. , и ищем треугольники на этих графиках. Медиана любого такого треугольника должна быть общим соседом трех вершин треугольника; если этого общего соседа не существует, граф не является медианным графом. Если все треугольники, найденные таким способом, имеют медианы, и предыдущий алгоритм обнаруживает, что граф удовлетворяет всем остальным условиям медианного графа, то на самом деле он должен быть медианным графом. Этот алгоритм требует не только возможности проверить, существует ли треугольник, но и списка всех треугольников на графике уровня. В произвольных графах перечисление всех треугольников иногда требует времени Ω( m 3/2 ), поскольку в некоторых графах такое количество треугольников, однако Hagauer et al. показывают, что количество треугольников, возникающих на графиках уровней их приведения, близко к линейному, что позволяет Alon et al. Метод быстрого нахождения треугольников, основанный на умножении матриц.
Филогения — это вывод эволюционных деревьев из наблюдаемых характеристик видов ; такое дерево должно помещать виды в отдельные вершины и может иметь дополнительные скрытые вершины , но скрытые вершины должны иметь три или более инцидентных ребра и также должны быть помечены характеристиками. Характеристика является бинарной, когда она имеет только два возможных значения, а набор видов и их характеристик демонстрирует идеальную филогению , когда существует эволюционное дерево, в котором вершины (виды и скрытые вершины), помеченные каким-либо конкретным значением характеристики, образуют непрерывное поддерево. Если дерево с идеальной филогенией невозможно, часто желательно найти дерево, демонстрирующее максимальную экономию или, что то же самое, минимизирующее количество раз, когда конечные точки ребра дерева имеют разные значения для одной из характеристик, суммированных по всем ребрам и всем характеристики.
Бунеман (1971) описал метод определения идеальной филогении бинарных характеристик, если они существуют. Его метод естественным образом обобщается до построения медианного графа для любого набора видов и бинарных характеристик, который получил название медианной сети или графа Бунемана [24] и является разновидностью филогенетической сети . Каждое эволюционное дерево максимальной экономии встраивается в граф Бунемана в том смысле, что ребра дерева следуют по путям в графе, а количество изменений характеристического значения на ребре дерева такое же, как и число на соответствующем пути. Граф Бунемана будет деревом тогда и только тогда, когда существует совершенная филогения; это происходит тогда, когда не существует двух несовместимых характеристик, для которых наблюдаются все четыре комбинации значений характеристик.
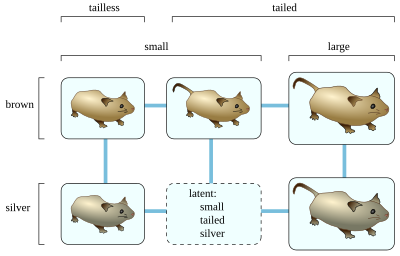
Чтобы сформировать граф Бунемана для набора видов и характеристик, сначала исключите избыточные виды, неотличимые от некоторых других видов, и избыточные характеристики, которые всегда совпадают с некоторой другой характеристикой. Затем сформируйте скрытую вершину для каждой комбинации характеристических значений так, чтобы каждые два значения существовали у некоторых известных видов. В показанном примере есть маленькие коричневые бесхвостые мыши, маленькие серебряные бесхвостые мыши, маленькие коричневые мыши с коричневым хвостом, большие коричневые мыши с коричневым хвостом и большие мыши с серебряным хвостом; метод графа Бунемана формирует скрытую вершину, соответствующую неизвестному виду маленьких мышей с серебряным хвостом, поскольку каждая парная комбинация (маленькая и серебряная, маленькая и хвостатая, серебряная и хвостатая) наблюдается у некоторых других известных видов. Однако этот метод не позволяет сделать вывод о существовании крупных коричневых бесхвостых мышей, поскольку неизвестно, чтобы ни одна мышь обладала одновременно большими и бесхвостыми признаками. Как только скрытые вершины определены, сформируйте ребро между каждой парой видов или скрытых вершин, которые отличаются одной характеристикой.
Эквивалентно можно описать набор бинарных характеристик как разделенную систему , семейство множеств, обладающее тем свойством, что дополняющее множество каждого множества в семействе также находится в семействе. Эта разделенная система имеет набор для каждого значения характеристики, состоящий из видов, имеющих это значение. При включении скрытых вершин результирующая система разбиения обладает свойством Хелли : каждое попарно пересекающееся подсемейство имеет общее пересечение. В некотором смысле медианные графы характеризуются как происходящие из систем расщепления Хелли: пары ( W uv , W vu ), определенные для каждого ребра uv медианного графа, образуют систему расщепления Хелли, поэтому, если к этой системе применить конструкцию графа Бунемана, нет потребуются скрытые вершины, и результат будет таким же, как и в исходном графе. [25]
Бандельт и др. (1995) и Бандельт, Маколей и Ричардс (2000) описывают методы упрощенного ручного расчета графика Бунемана и используют эту конструкцию для визуализации генетических взаимоотношений человека.
