Многомерная выборка

В цифровой обработке сигналов многомерная выборка — это процесс преобразования функции многомерной переменной в дискретный набор значений функции, измеренных на дискретном наборе точек. В этой статье представлен основной результат Петерсена и Миддлтона ^[1] об условиях идеального восстановления функции, ограниченной волновым числом , по ее измерениям на дискретной решетке точек. Этот результат, также известный как теорема Петерсена-Миддлтона , является обобщением теоремы выборки Найквиста-Шеннона для выборки одномерных функций , ограниченных полосой , в многомерные евклидовы пространства .

По сути, теорема Петерсена-Миддлтона показывает, что функция, ограниченная волновым числом, может быть идеально восстановлена ​​по ее значениям на бесконечной решетке точек, при условии, что решетка достаточно мелкая. Теорема дает условия на решетке, при которых возможна идеальная реконструкция.

Как и в случае с теоремой выборки Найквиста-Шеннона, эта теорема также предполагает идеализацию любой реальной ситуации, поскольку она применима только к функциям, выборка которых осуществляется из бесконечного числа точек. Идеальная реконструкция математически возможна для идеализированной модели, но является лишь приближением для реальных функций и методов выборки, хотя на практике часто бывает очень хорошей.

Предварительные сведения

Рис. 1: Шестиугольная решетка выборки и ее базисные векторы v ₁ и v ₂ ${\displaystyle \Lambda }$

Рис. 2: Обратная решетка , соответствующая решетке на рис. 1, и ее базисные векторы u ₁ и u ₂ (рисунок не в масштабе). ${\displaystyle \Gamma }$ ${\displaystyle \Lambda }$

Понятие функции с ограниченной полосой пропускания в одном измерении можно обобщить до понятия функции с ограниченной волновым числом в более высоких измерениях. Напомним, что преобразование Фурье интегрируемой функции в n -мерном евклидовом пространстве определяется как: ${\displaystyle f(\cdot )}$

${\displaystyle {\hat {f}}(\xi )={\mathcal {F}}(f)(\xi )=\int _{\Re ^{n}}f(x)e^{-2\pi i\langle x,\xi \rangle }\,dx}$

где x и ξ — n -мерные векторы , а — скалярное произведение векторов. Функция называется ограниченной по волновому числу набором, если преобразование Фурье удовлетворяет условиям . ${\displaystyle \langle x,\xi \rangle }$ ${\displaystyle f(\cdot )}$ ${\displaystyle \Omega }$ ${\displaystyle {\hat {f}}(\xi )=0}$ ${\displaystyle \xi \notin \Omega }$

Аналогичным образом, конфигурация равномерно расположенных точек выборки в одномерном измерении может быть обобщена до решетки в более высоких измерениях. Решетка — это совокупность точек вида , где { v ₁ , ..., v _n } является базой для . Обратная решетка, соответствующая , определяется формулой ${\displaystyle \Lambda \subset \Re ^{n}}$ ${\displaystyle \Lambda =\left\{\sum _{i=1}^{n}a_{i}v_{i}\;|\;a_{i}\in \mathbb {Z} \right\}}$ ${\displaystyle \Re ^{n}}$ ${\displaystyle \Gamma }$ ${\displaystyle \Lambda }$

${\displaystyle \Gamma =\left\{\sum _{i=1}^{n}a_{i}u_{i}\;|\;a_{i}\in \mathbb {Z} \right\}}$

где векторы выбраны так, чтобы удовлетворить . То есть, если векторы образуют столбцы матрицы и столбцы матрицы , то . Примером решетки выборки в двумерном пространстве является шестиугольная решетка, изображенная на рисунке 1. Соответствующая обратная решетка показана на рисунке 2. Обратная решетка квадратной решетки в двух измерениях представляет собой еще одну квадратную решетку. В трехмерном пространстве обратная решетка гранецентрированной кубической (FCC) решетки представляет собой объемноцентрированную кубическую (BCC) решетку. ${\displaystyle u_{i}}$ ${\displaystyle \langle u_{i},v_{j}\rangle =\delta _{ij}}$ ${\displaystyle u_{i}}$ ${\displaystyle A}$ ${\displaystyle v_{i}}$ ${\displaystyle B}$ ${\displaystyle A=B^{-T}}$

Теорема

Обозначим решетку в и соответствующую обратную решетку. Теорема Петерсена и Миддлтона ^[1] утверждает, что функция , ограниченная набором по волновому числу, может быть точно восстановлена ​​по ее измерениям при условии, что набор не перекрывается ни с одной из его сдвинутых версий , где сдвиг x представляет собой любой ненулевой элемент. обратной решетки . Другими словами, может быть точно восстановлено по его измерениям при условии, что для всех . ${\displaystyle \Lambda }$ ${\displaystyle \Re ^{n}}$ ${\displaystyle \Gamma }$ ${\displaystyle f(\cdot )}$ ${\displaystyle \Omega \subset \Re ^{n}}$ ${\displaystyle \Lambda }$ ${\displaystyle \Omega }$ ${\displaystyle \Omega +x}$ ${\displaystyle \Gamma }$ ${\displaystyle f(\cdot )}$ ${\displaystyle \Lambda }$ ${\displaystyle \Omega \cap \{x+y:y\in \Omega \}=\emptyset }$ ${\displaystyle x\in \Gamma \setminus \{0\}}$

Реконструкция

Рис. 3: Поддержка дискретизированного спектра , полученного путем гексагональной дискретизации двумерной функции, ограниченной волновым числом круглого диска. Синий круг представляет собой поддержку исходного поля с ограниченным волновым числом, а зеленые круги представляют повторения. В этом примере спектральные повторения не перекрываются и, следовательно, нет наложения спектров. Исходный спектр может быть точно восстановлен из дискретного спектра. ${\displaystyle {\hat {f}}_{s}(\cdot )}$ ${\displaystyle \Omega }$

Обобщение формулы суммирования Пуассона на более высокие размерности ^[2] можно использовать, чтобы показать, что выборки функции на решетке достаточны для создания периодического суммирования функции . Результат: ${\displaystyle \{f(x):x\in \Lambda \}}$ ${\displaystyle f(\cdot )}$ ${\displaystyle \Lambda }$ ${\displaystyle {\hat {f}}(\cdot )}$

где представляет собой объем параллелепипеда , образованного векторами { v ₁ , ..., v _n }. Эту периодическую функцию часто называют дискретным спектром, и ее можно интерпретировать как аналог преобразования Фурье с дискретным временем (DTFT) в более высоких измерениях. Если исходный спектр, ограниченный волновым числом, поддерживается на множестве, то функция поддерживается на периодических повторениях сдвинутых на точки обратной решетки . Если условия теоремы Петерсена-Миддлтона выполнены, то функция равна при всех , а значит, исходное поле можно точно восстановить по выборкам. В этом случае восстановленное поле соответствует исходному полю и может быть выражено через выборки как ${\displaystyle |\Lambda |}$ ${\displaystyle {\hat {f}}(\cdot )}$ ${\displaystyle \Omega }$ ${\displaystyle {\hat {f}}_{s}(\cdot )}$ ${\displaystyle \Omega }$ ${\displaystyle \Gamma }$ ${\displaystyle {\hat {f}}_{s}(\xi )}$ ${\displaystyle {\hat {f}}(\xi )}$ ${\displaystyle \xi \in \Omega }$

где – обратное преобразование Фурье характеристической функции множества . Эта интерполяционная формула является многомерным эквивалентом интерполяционной формулы Уиттекера-Шеннона . ${\displaystyle {\check {\chi }}_{\Omega }(\cdot )}$ ${\displaystyle \Omega }$

В качестве примера предположим, что это круглый диск. Рисунок 3 иллюстрирует поддержку условий теоремы Петерсена-Миддлтона. Мы видим, что повторения спектров не перекрываются и, следовательно, исходный спектр может быть точно восстановлен. ${\displaystyle \Omega }$ ${\displaystyle {\hat {f}}_{s}(\cdot )}$

Подразумеваемое

Псевдонимы

Рис. 4: Поддержка дискретизированного спектра , полученного путем гексагональной дискретизации двумерной функции, ограниченной волновым числом круглого диска. В этом примере решетка дискретизации недостаточно мелкая, и, следовательно, диски перекрываются в дискретизированном спектре. Таким образом, спектр , представленный синим кружком, не может быть точно восстановлен из-за наложения повторений (показано зеленым), что приводит к наложению спектров. ${\displaystyle {\hat {f}}_{s}(\cdot )}$ ${\displaystyle \Omega }$

Рис. 5: Пространственное сглаживание в виде муарового узора .

Рис. 6: Правильно выбранное изображение кирпичной стены.

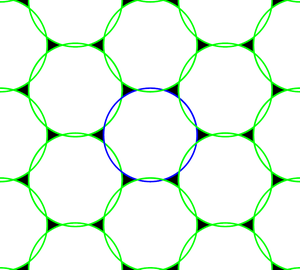
Теорема дает условия для решеток выборки для идеального восстановления выборки. Если решетки недостаточно мелкие, чтобы удовлетворить условию Петерсена-Миддлтона, то поле вообще невозможно точно восстановить по образцам. В этом случае мы говорим, что образцы могут иметь псевдонимы . Опять же, рассмотрим пример круглого диска. Если условия Петерсена-Миддлтона не выполняются, поддержка дискретного спектра будет такой, как показано на рисунке 4. В этом случае спектральные повторения перекрываются, что приводит к наложению спектров при реконструкции. ${\displaystyle \Omega }$

Простую иллюстрацию алиасинга можно получить, изучая изображения с низким разрешением. Изображение в оттенках серого можно интерпретировать как функцию в двумерном пространстве. Пример наложения псевдонимов показан на изображениях кирпичных узоров на рисунке 5. На изображении показаны эффекты наложения псевдонимов, когда условие теоремы выборки не выполняется. Если решетка пикселей недостаточно мелкая для сцены, происходит алиасинг, о чем свидетельствует появление муарового узора на полученном изображении. Изображение на рисунке 6 получено, когда сглаженная версия сцены выбрана с той же решеткой. В этом случае условия теоремы выполняются и наложения спектров не происходит.

Оптимальные решетки выборки

Одним из объектов интереса при разработке схемы отбора проб для полей с ограниченным волновым числом является определение конфигурации точек, приводящей к минимальной плотности отбора проб, т. е. плотности точек отбора проб на единицу пространственного объема в . Обычно стоимость проведения и хранения измерений пропорциональна используемой плотности выборки. Часто на практике естественным подходом к выборке двумерных полей является выборка в точках прямоугольной решетки . Однако это не всегда идеальный выбор с точки зрения плотности выборки. Теорему Петерсена и Миддлтона можно использовать для определения оптимальной решетки для полей выборки, которые ограничены по волновому числу заданным набором . Например, можно показать, что решетка с минимальной пространственной плотностью точек, допускающая совершенные реконструкции полей, ограниченных волновым числом кругового диска, представляет собой гексагональную решетку. ^[3] Как следствие, гексагональные решетки являются предпочтительными для выборки изотропных полей в . ${\displaystyle \Re ^{n}}$ ${\displaystyle \Omega \subset \Re ^{d}}$ ${\displaystyle \Re ^{2}}$ ${\displaystyle \Re ^{2}}$ ${\displaystyle \Re ^{2}}$

Оптимальные решетки выборки изучались в более высоких размерностях. ^[4] Как правило, оптимальные решетки упаковки сфер идеальны для выборки гладких случайных процессов, тогда как оптимальные решетки, покрывающие сферы ^[5] , идеальны для выборки грубых случайных процессов.

Поскольку оптимальные решетки, как правило, неразделимы, разработка фильтров интерполяции и реконструкции требует механизмов проектирования фильтров без тензорного произведения (т. е. неразделимых). Коробчатые сплайны обеспечивают гибкую основу для разработки таких неразделимых КИХ- фильтров реконструкции, которые можно геометрически адаптировать для каждой решетки. ^{[6] [7]} Шестнадцатеричные сплайны ^[8] являются обобщением B-сплайнов для двумерных гексагональных решеток. Аналогичным образом, в трехмерных и более высоких измерениях сплайны Вороного ^[9] представляют собой обобщение B-сплайнов , которые можно использовать для разработки неразделимых КИХ-фильтров, геометрически адаптированных для любой решетки, включая оптимальные решетки.

Явное построение идеальных фильтров нижних частот (т. е. функций sinc ), обобщенных на оптимальные решетки, возможно путем изучения геометрических свойств зон Бриллюэна (т. е. указанных выше) этих решеток (которые являются зонотопами ). ^[10] Этот подход обеспечивает явное представление в замкнутой форме для общих решеток, включая оптимальные решетки выборки. Эта конструкция обеспечивает обобщение одномерного фильтра Ланцоша на многомерную настройку для оптимальных решеток. ^[10] ${\displaystyle \Omega }$ ${\displaystyle {\check {\chi }}_{\Omega }(\cdot )}$

Приложения

Теорема Петерсена-Миддлтона полезна при разработке эффективных стратегий размещения датчиков в приложениях, связанных с измерением пространственных явлений, таких как сейсмические исследования, мониторинг окружающей среды и измерения пространственного звукового поля. ^[11]

Рекомендации

1. Д. П. Петерсен и Д. Миддлтон, «Выборка и реконструкция функций с ограниченным волновым числом в N-мерных евклидовых пространствах», Information and Control, vol. 5, стр. 279–323, 1962.
2. EM Stein и G. Weiss, «Введение в анализ Фурье евклидовых пространств», Princeton University Press, Принстон, 1971.
3. Д. Р. Мерсеро, «Обработка двумерных сигналов с гексагональной выборкой», Proceedings of the IEEE, vol. 67, нет. 6, стр. 930–949, июнь 1979 г.
4. Кунш, HR; Агрелл, Э.; Хампрехт, ФА (2005). «Оптимальные решетки для выборки». Транзакции IEEE по теории информации . 51 (2): 634. doi :10.1109/TIT.2004.840864.
5. Дж. Х. Конвей, NJA Слоан. Сферические упаковки, решетки и группы. Спрингер, 1999.
6. А. Энтезари. Оптимальные решетки выборки и трехмерные сплайны. [Ванкувер, Британская Колумбия]: Университет Саймона Фрейзера, 2007. <http://summit.sfu.ca/item/8178>.
7. Энтезари, А.; Ван Де Виль, Д.; Моллер, Т. (2008). «Практические коробчатые сплайны для реконструкции на телецентрированной кубической решетке». Транзакции IEEE по визуализации и компьютерной графике . 14 (2): 313–328. CiteSeerX 10.1.1.330.3851 . дои : 10.1109/TVCG.2007.70429. ПМИД  18192712. 
8. Ван Де Виль, Д.; Блу, Т.; Унсер, М.; Филипс, В.; Лемахье, И.; Ван Де Валле, Р. (2004). «Шестиугольные сплайны: новое семейство сплайнов для шестиугольных решеток». Транзакции IEEE при обработке изображений . 13 (6): 758–772. дои : 10.1109/TIP.2004.827231. ПМИД  15648867.
9. Мирзаргар, М.; Энтезари, А. (2010). «Сплайны Вороного». Транзакции IEEE по обработке сигналов . 58 (9): 4572. doi :10.1109/TSP.2010.2051808.
10. Йе, В.; Энтезари, А. (2012). «Геометрическое построение многомерных функций Sinc». Транзакции IEEE при обработке изображений . 21 (6): 2969–2979. дои : 10.1109/TIP.2011.2162421. ПМИД  21775264.
11. Бардан, В. (11 июня 2007 г.). «Теорема Петерсена-Миддлтона и выборка сейсмических данных». Европейская ассоциация геологов и инженеров: ср. дои : 10.3997/2214-4609.201401831. ISBN 978-90-73781-54-2. {{cite journal}}: Требуется цитировать журнал |journal=( помощь )