Мост осла

Утверждение, что углы, противолежащие равным сторонам равнобедренного треугольника, сами по себе равны

Мост осинового моста в издании «Начал» Оливера Бирна ^[1]

В геометрии теорема о том, что углы, противолежащие равным сторонам равнобедренного треугольника, сами равны, известна как pons asinorum ( / ˈ p ɒ n z ˌ æ s ɪ ˈ n ɔːr ə m / PONZ ass-ih- NOR -əm ), по-латыни «мост ослов », или более описательно как теорема о равнобедренном треугольнике . Теорема появляется как Предложение 5 Книги 1 в «Началах » Евклида . [ ^1] Обратное утверждение также верно: если два угла треугольника равны , то и противолежащие им стороны также равны.

Pons asinorum также используется метафорически для проблемы или вызова, которые действуют как проверка критического мышления , ссылаясь на способность «ослиного моста» разделять способных и неспособных мыслить. Его первое известное использование в этом контексте относится к 1645 году. ^[2]

Этимология

Существует два распространенных объяснения названия pons asinorum , самое простое из которых заключается в том, что используемая диаграмма напоминает физический мост . Но более популярное объяснение заключается в том, что это первый настоящий тест в Элементах интеллекта читателя и он выполняет функцию «моста» к более сложным предложениям, которые следуют далее. ^[3]

Другим средневековым термином для теоремы о равнобедренном треугольнике был Elefuga , который, по мнению Роджера Бэкона , происходит от греческого elegia «несчастье» и латинского fuga «полет», то есть «полет негодяев». Хотя эта этимология сомнительна, она перекликается с использованием Чосером термина «flemyng of wreches» для этой теоремы. ^[4]

Имя Дулькарнон было дано 47-му предложению Книги I Евклида, более известному как теорема Пифагора , от арабского Dhū 'l qarnain ذُو ٱلْقَرْنَيْن, что означает «владелец двух рогов», потому что диаграммы теоремы показывали два меньших квадрата, похожих на рога, в верхней части рисунка. Этот термин также использовался как метафора для дилеммы. ^[4] Название pons asinorum само по себе иногда применялось к теореме Пифагора. ^[5]

Карл Фридрих Гаусс предположительно однажды предположил, что понимание личности Эйлера может играть аналогичную роль, как критерий, указывающий, может ли кто-то стать первоклассным математиком . ^[6]

Доказательства

Евклид и Прокл

Утверждение Евклида о pons asinorum включает второй вывод о том, что если равные стороны треугольника продолжены ниже основания, то углы между продолжениями и основанием также равны. Доказательство Евклида включает в себя проведение вспомогательных линий к этим продолжениям. Но, как указывает комментатор Евклида Прокл , Евклид никогда не использует второй вывод, и его доказательство можно несколько упростить, проведя вместо этого вспомогательные линии к сторонам треугольника, остальная часть доказательства проводится более или менее таким же образом.

Было много предположений и споров о том, почему Евклид добавил второй вывод к теореме, учитывая, что это усложняет доказательство. Одно правдоподобное объяснение, данное Проклом, состоит в том, что второй вывод может быть использован в возможных возражениях против доказательств более поздних предложений, где Евклид не охватывает все случаи. ^[7] Доказательство в значительной степени опирается на то, что сегодня называется сторона-угол-сторона (SAS), предыдущее предложение в « Началах» , которое гласит, что даны два треугольника, для которых две пары соответствующих сторон и их включенные углы соответственно равны , то треугольники равны.

Вариация Прокла доказательства Евклида выглядит следующим образом: ^[8] Пусть ⁠ ⁠ ${\displaystyle \triangle ABC}$ будет равнобедренным треугольником с конгруэнтными сторонами ⁠ ⁠ ${\displaystyle AB\cong AC}$ . Выберите произвольную точку ⁠ ⁠ ${\displaystyle D}$ вдоль стороны ⁠ ⁠ , ${\displaystyle AB}$ а затем постройте точку ⁠ ⁠ ${\displaystyle E}$ на ⁠ ⁠ , ${\displaystyle AC}$ чтобы получить конгруэнтные отрезки ⁠ ⁠ ${\displaystyle AD\cong AE}$ . Начертите вспомогательные отрезки ⁠ ⁠ ${\displaystyle BE}$ , ⁠ ⁠ ${\displaystyle DC}$ , и ⁠ ⁠ ${\displaystyle DE}$ . По стороне-углу-стороне треугольники ⁠ ⁠ ${\displaystyle \triangle BAE\cong \triangle CAD}$ . Следовательно ⁠ ⁠ ${\displaystyle \angle ABE\cong \angle ACD}$ , ⁠ ⁠ ${\displaystyle \angle ADC\cong \angle AEB}$ , и ⁠ ⁠ ${\displaystyle BE\cong CD}$ . Вычитая конгруэнтные отрезки, ⁠ ⁠ ${\displaystyle BD\cong CE}$ . Это устанавливает еще одну пару равных треугольников, ⁠ ⁠ ${\displaystyle \triangle DBE\cong \triangle ECD}$ , снова по стороне-углу-стороне. Следовательно ⁠ ⁠ ${\displaystyle \angle BDE\cong \angle CED}$ и ⁠ ⁠ ${\displaystyle \angle BED\cong \angle CDE}$ . Вычитая равные углы, ⁠ ⁠ ${\displaystyle \angle BDC\cong \angle CEB}$ . Наконец ⁠ ⁠ ${\displaystyle \triangle BDC\cong \triangle CEB}$ третьим применением стороны-угла-стороны. Следовательно ⁠ ⁠ ${\displaystyle \angle CBD\cong \angle BCE}$ , что и требовалось доказать.

Паппус

Прокл дает гораздо более короткое доказательство, приписываемое Паппу Александрийскому . Оно не только проще, но и не требует вообще никаких дополнительных построений. Метод доказательства заключается в применении стороны-угла-стороны к треугольнику и его зеркальному отображению. Более современные авторы, подражая методу доказательства, данному для предыдущего предложения, описывают это как взятие треугольника, переворачивание его и укладывание его на себя. ^{[9] [10]} Этот метод высмеивается Чарльзом Доджсоном в «Евклиде и его современных соперниках » , называя его « ирландским быком », потому что он, по-видимому, требует, чтобы треугольник находился в двух местах одновременно. ^[11]

Доказательство следующее: ^[12] Пусть ABC — равнобедренный треугольник с равными сторонами AB и AC . Рассмотрим треугольники ABC и ACB , где ACB рассматривается как второй треугольник с вершинами A , C и B, соответствующими соответственно A , B и C в исходном треугольнике. равен самому себе, AB  =  AC и AC  =  AB , поэтому по отношению сторона-угол-сторона треугольники ABC и ACB равны. В частности, . ^[13] ${\displaystyle \angle A}$ ${\displaystyle \angle B=\angle C}$

Другие

Доказательство из учебника

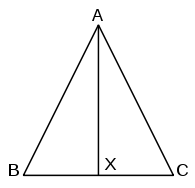
Стандартный метод из учебника заключается в построении биссектрисы угла в точке A. [ ^14] Это проще, чем доказательство Евклида, но Евклид не представляет построение биссектрисы угла до предложения 9. Поэтому порядок представления предложений Евклида пришлось бы изменить, чтобы избежать возможности циклического рассуждения.

Доказательство проводится следующим образом: ^[15] Как и прежде, пусть треугольник ABC с AB  =  AC . Постройте биссектрису угла и продолжим ее до пересечения с BC в точке X . AB  =  AC и AX равен самому себе. Более того, , поэтому, применяя функцию сторона-угол-сторона, треугольники BAX и CAX равны. Отсюда следует, что углы при B и C равны. ${\displaystyle \angle BAC}$ ${\displaystyle \angle BAX=\angle CAX}$

Лежандр использует похожую конструкцию в «Элементах геометрии» , но беря X за середину BC . ^[16] Доказательство похоже, но вместо «сторона -угол-сторона» следует использовать «сторона-сторона », а «сторона-сторона» не приводится Евклидом до более поздних «Элементов » .

В 1876 году, будучи членом Конгресса США , будущий президент Джеймс А. Гарфилд разработал доказательство с использованием трапеции, которое было опубликовано в New England Journal of Education . ^[17] Историк математики Уильям Данхэм писал, что работа Гарфилда с трапецией была «действительно очень умным доказательством». ^[18] Согласно Journal , Гарфилд пришёл к доказательству «во время математических развлечений и дискуссий с другими членами конгресса». ^[19]

Во внутренних пространствах продукта

Теорема о равнобедренном треугольнике справедлива в пространствах внутреннего произведения над действительными или комплексными числами . В таких пространствах, при заданных векторах x , y и z , теорема гласит, что если и то ${\displaystyle x+y+z=0}$ ${\displaystyle \|x\|=\|y\|,}$ ${\displaystyle \|x-z\|=\|y-z\|.}$

Поскольку и где θ — угол между двумя векторами, заключение этой теоремы в форме внутреннего произведения эквивалентно утверждению о равенстве углов. ${\displaystyle \|x-z\|^{2}=\|x\|^{2}-2x\cdot z+\|z\|^{2}}$ ${\displaystyle x\cdot z=\|x\|\|z\|\cos \theta ,}$

Метафорическое использование

Использование pons asinorum в качестве метафоры для проверки критического мышления включает в себя:

• В «Филобиблоне » Ричарда Онгервилля XIV века содержится отрывок «Quot Euclidis discipulos Retrojecit Elefuga quasi scopulos eminens et abruptus, qui nullo scalarum suffragio scandi posset! Durus, inquiunt, est his sermo; quis potest eum audire?», в котором теорема сравнивается с крутой утес, на который не поможет никакая лестница, и спрашивает, сколько потенциальным геометрам отказали. ^[4]
• Термин pons asinorum , в обоих своих значениях — как мост и как тест, — используется как метафора для нахождения среднего термина силлогизма . [ ^4]
• Поэт XVIII века Томас Кэмпбелл написал юмористическую поэму под названием «Pons asinorum», в которой класс геометрии нападает на теорему, подобно тому, как отряд солдат атакует крепость; битва не обошлась без потерь. ^[20]
• Экономист Джон Стюарт Милль назвал закон ренты Рикардо pons asinorum экономики. ^[21]
• Финское aasinsilta и шведское åsnebrygga — это литературный прием, при котором слабая, даже надуманная связь между двумя аргументами или темами, которая является почти, но не совсем non sequitur , используется как неловкий переход между ними. В серьезном тексте это считается стилистической ошибкой, поскольку она по праву принадлежит стилю потока сознания — или causerie . Типичные примеры — завершение раздела сообщением о том, о чем будет следующий раздел, без объяснения того, почему темы связаны, расширение случайного упоминания до подробного рассмотрения или нахождение надуманной связи между темами (например, «Мы купили красного вина; говоря о красных жидкостях, завтра Всемирный день донора крови»).
• В голландском языке ezelsbruggetje ( 'мост ослов') — это слово для обозначения мнемоники . То же самое относится и к немецкому Eselsbrücke .
• В чешском языке oslí můstek имеет два значения: оно может описывать либо вымышленную связь между двумя темами, либо мнемонический прием.

Миф о несостоятельности искусственного интеллекта

Устойчивая часть математического фольклора утверждает, что программа искусственного интеллекта обнаружила оригинальное и более элегантное доказательство этой теоремы. ^{[22] [23]} Фактически, Марвин Мински рассказывает, что он заново открыл доказательство Паппуса (о котором он не знал), смоделировав то, что может сделать механическая доказательная машина теорем. ^{[24] [10]}

Примечания

1. Бирн, Оливер (1847). Первые шесть книг «Начал Евклида», в которых для большего удобства учащихся вместо букв используются цветные диаграммы и символы . Taschen. стр. Страница 5. ISBN 978-1528770439.
2. "Pons asinorum". Словарь Merriam-Webster.com .
3. DE Smith История математики (1958 Дувр) стр. 284
4. AF West & HD Thompson "On Dulcarnon, Elefuga And Pons Asinorum as anciful names for geometrical propositions" Бюллетень Принстонского университета , том 3, № 4 (1891), стр. 84
5. Смит, Дэвид Юджин (1925). История математики. Т. 2. Ginn & Co. стр. 284, сноска 1.
6. Дербишир, Джон (2003). Одержимость главным: Бернхард Риман и величайшая нерешенная проблема в математике . 500 Fifth Street, NW, Вашингтон, округ Колумбия, 20001: Joseph Henry Press. стр. 202. ISBN 0-309-08549-7. первоклассный математик.{{cite book}}: CS1 maint: location (link)
7. Хит, стр. 251–255.
8. Следуя Проклу, стр. 53
9. Например, Ф. Катбертсон «Основы геометрии» (1876 Оксфорд), стр. 7
10. Майкл А. Б. Дикин, «От Паппуса до наших дней: история доказательства», The Mathematical Gazette 74 :467:6-11 (март 1990 г.) JSTOR  3618841
11. Чарльз Лютвидж Доджсон, Эвклид и его современные соперники, акт I, сцена II, §6
12. Следуя Проклу, стр. 54
13. Хит стр. 254 для раздела
14. Например, Дж. М. Уилсон Элементарная геометрия (1878 Оксфорд) стр. 20
15. Вслед за Уилсоном
16. AM Legendre Éléments de géométrie (Libr. de Firmin-Didot et Cie, 1876 г.), с. 14
17. Г., Дж. А. (1876). «Понс Асинорум». Образовательный журнал Новой Англии . 3 (14): 161. ISSN  2578-4145. JSTOR  44764657.
18. Данэм, Уильям (1994). Математическая вселенная: алфавитное путешествие по великим доказательствам, проблемам и личностям . Wiley & Sons. стр. 99. Bibcode : 1994muaa.book.....D. ISBN 9780471536567.
19. Колпас, Сид Дж. «Математическое сокровище: доказательство теоремы Пифагора Гарфилда». Математическая ассоциация Америки. Архивировано из оригинала 6 декабря 2021 г. Получено 22 декабря 2021 г.
20. Кэмпбелл, Томас (1864). Поэтические произведения Томаса Кэмпбелла. Литтл, Браун.
21. Джон Стюарт Милль «Принципы политической экономии» (1866: Лонгманс, Грин, Ридер и Дайер), Книга 2, Глава 16, стр. 261
22. Яакко Хинтикка, «О творчестве в рассуждениях», в книге Аке Э. Андерссона, Н. Е. Сахлина, ред., « Сложность творчества» , 2013, ISBN 9401587884 , стр. 72 
23. А. Баттерсби, Математика в менеджменте , 1966, цитируется в Дикине
24. Джереми Бернстайн, «Профили: ИИ» (интервью с Марвином Мински), The New Yorker 14 декабря 1981 г., стр. 50-126

Ссылки

• Евклид, комментарий и перевод Т. Л. Хита Элементы Том 1 (1908 Кембридж) Google Книги
• Евклид, комментарий Прокла , ред. и перевод Т. Тейлора Элементы, т. 2 (1789) Google Книги

Внешние ссылки

• Pons asinorum на PlanetMath .
• Представление Д.Э. Джойсом «Начал» Евклида