В информатике преобразование графа или переписывание графа относится к технике создания нового графа из исходного графа алгоритмическим путем. Он имеет многочисленные приложения, начиная от разработки программного обеспечения ( конструирование программного обеспечения , а также проверка программного обеспечения ) и заканчивая алгоритмами компоновки и генерацией изображений.
Преобразования графов можно использовать в качестве абстракции вычислений. Основная идея заключается в том, что если состояние вычисления можно представить в виде графа, то дальнейшие шаги в этом вычислении можно представить в виде правил преобразования на этом графе. Такие правила состоят из исходного графа, который должен быть сопоставлен с подграфом в полном состоянии, и заменяющего графа, который заменит сопоставленный подграф.
Формально система переписывания графа обычно состоит из набора правил переписывания графа вида , называемого графом шаблона (или левой стороной) и называемого графом замены (или правой стороной правила). Правило переписывания графа применяется к главному графу путем поиска вхождения графа шаблона ( сопоставления с шаблоном , таким образом решая проблему изоморфизма подграфа ) и замены найденного вхождения экземпляром графа замены. Правила переписывания могут быть дополнительно упорядочены в случае маркированных графов , например, в грамматиках графов с регулировкой строк.
Иногда графовая грамматика используется как синоним системы переписывания графов , особенно в контексте формальных языков ; различные формулировки используются для того, чтобы подчеркнуть цель конструкций, например, перечисление всех графов из некоторого начального графа, т. е. генерацию графового языка, а не просто преобразование заданного состояния (хост-графа) в новое состояние.
Алгебраический подход к переписыванию графа основан на теории категорий . Алгебраический подход далее делится на подподходы, наиболее распространенными из которых являются подход с двойным выталкиванием (DPO) и подход с одиночным выталкиванием (SPO) . Другие подподходы включают подход с полуторакратным выталкиванием и подход с вытягиванием .
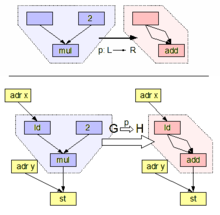
С точки зрения подхода DPO правило переписывания графа представляет собой пару морфизмов в категории графов и гомоморфизмов графов между ними: , также записываемое как , где является инъективным . Граф K называется инвариантным или иногда графом склеивания . Шаг переписывания или применение правила r к главному графу G определяется двумя диаграммами выталкивания , обе из которых происходят из одного и того же морфизма , где D является контекстным графом (отсюда и название double -pushout). Другой морфизм графа моделирует вхождение L в G и называется соответствием . Практическое понимание этого заключается в том, что представляет собой подграф, который сопоставляется с (см. проблему изоморфизма подграфов ), и после того, как соответствие найдено, заменяется на в главном графе , где служит интерфейсом, содержащим узлы и ребра, которые сохраняются при применении правила. Граф необходим для присоединения сопоставляемого шаблона к его контексту: если он пуст, соответствие может обозначать только целый связный компонент графа .
В отличие от этого, правило переписывания графа подхода SPO является единственным морфизмом в категории помеченных мультиграфов и частичных отображений , которые сохраняют структуру мультиграфа: . Таким образом, шаг переписывания определяется единственной диаграммой выталкивания . Практическое понимание этого похоже на подход DPO. Разница в том, что нет интерфейса между графом-хозяином G и графом G', являющимся результатом шага переписывания.
С практической точки зрения, ключевое различие между DPO и SPO заключается в том, как они справляются с удалением узлов со смежными ребрами, в частности, как они избегают того, что такие удаления могут оставить после себя «висячие ребра». Подход DPO удаляет узел только тогда, когда правило указывает на удаление всех смежных ребер (это условие висячих ребер можно проверить для заданного соответствия), тогда как подход SPO просто удаляет смежные ребра, не требуя явного указания.
Существует также другой алгебраический подход к переписыванию графов, основанный в основном на булевой алгебре и алгебре матриц, называемый грамматиками матричных графов . [1]
Еще один подход к переписыванию графов, известный как детерминированное переписывание графов, возник из логики и теории баз данных . [2] В этом подходе графы рассматриваются как экземпляры базы данных, а операции переписывания — как механизм для определения запросов и представлений; следовательно, все переписывания должны давать уникальные результаты ( вплоть до изоморфизма ), и это достигается путем одновременного применения любого правила переписывания по всему графу, где бы оно ни применялось, таким образом, что результат действительно определяется однозначно.
Другим подходом к переписыванию графов является переписывание графов терминов , которое включает в себя обработку или преобразование графов терминов (также известных как абстрактные семантические графы ) с помощью набора правил синтаксической переписи.
Графы терминов являются важной темой в исследовании языков программирования, поскольку правила переписывания графов терминов способны формально выражать операционную семантику компилятора . Графы терминов также используются в качестве абстрактных машин, способных моделировать химические и биологические вычисления, а также графические исчисления, такие как модели параллелизма. Графы терминов могут выполнять автоматическую проверку и логическое программирование, поскольку они хорошо подходят для представления квантифицированных утверждений в логике первого порядка. Программное обеспечение для символического программирования является еще одним приложением для графов терминов, которые способны представлять и выполнять вычисления с абстрактными алгебраическими структурами, такими как группы, поля и кольца.
Конференция TERMGRAPH [3] полностью посвящена исследованиям в области переписывания графов термов и их применениям.
Системы переписывания графов естественным образом группируются в классы в соответствии с видом представления используемых графов и тем, как выражаются переписывания. Термин грамматика графов, иначе эквивалентный системе переписывания графов или системе замены графов, чаще всего используется в классификациях. Некоторые распространенные типы:
Графы — это выразительный, наглядный и математически точный формализм для моделирования объектов (сущностей), связанных отношениями; объекты представлены узлами, а отношения между ними — ребрами. Узлы и ребра обычно типизированы и атрибутированы. Вычисления в этой модели описываются изменениями в отношениях между сущностями или изменениями атрибутов элементов графа. Они кодируются в правилах перезаписи графа/преобразования графа и выполняются системами перезаписи графа/инструментами преобразования графа.