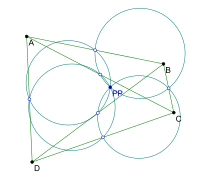
В геометрии точка Понселе четырех данных точек определяется следующим образом:
Пусть A, B, C, D — четыре точки на плоскости , которые не образуют ортоцентрическую систему и никакие три из них не лежат на одной прямой . Окружности девяти точек треугольников △ ABC , △ BCD , △ CDA , △ DAB пересекаются в одной точке — точке Понселе точек A, B, C, D. (Если A, B, C, D образуют ортоцентрическую систему, то треугольники △ ABC , △ BCD , △ CDA , △ DAB все имеют одну и ту же окружность девяти точек, а точка Понселе не определена.)
Если A, B, C, D не лежат на окружности, то точка Понселе точек A, B, C, D лежит на описанной окружности педального треугольника D относительно треугольника △ ABC и лежит на других аналогичных окружностях. (Если они лежат на окружности, то эти педальные треугольники будут прямыми; а именно, прямой Симсона D относительно треугольника △ ABC и других аналогичных прямых Симсона. В этом случае эти прямые по-прежнему пересекаются в точке Понселе, которая также будет антицентром вписанного четырехугольника , вершинами которого являются A, B, C, D. )
Точка Понселе A, B, C, D лежит на окружности, проходящей через пересечение прямых AB и CD , пересечение прямых AC и BD и пересечение прямых AD и BC (предполагается, что все эти пересечения существуют).
Точка Понселе A, B, C, D является центром уникальной прямоугольной гиперболы, проходящей через A, B, C, D.