Логическое равенство — это логический оператор , который сравнивает два значения истинности или, в более общем смысле, две формулы , так что он возвращает значение True, если оба аргумента имеют одинаковое значение истинности, и False, если они различны. В случае, когда формулы имеют свободные переменные , мы говорим, что две формулы равны, когда их значения истинности равны для всех возможных разрешений свободных переменных. Это соответствует равенству в булевой алгебре и логическому биусловию в исчислении высказываний .
В различных приложениях общепринятой практикой, хотя и не всегда технически точной, является обозначение операции логического равенства над логическими операндами x и y с помощью любой из следующих форм:
Однако некоторые логики проводят четкое различие между функциональной формой , подобной тем, что приведены в левом столбце, которую они интерпретируют как применение функции к паре аргументов — и, таким образом, простое указание на то, что значение составного выражения зависит от значений компонентных выражений, — и эквациональной формой , подобной тем, что приведены в правом столбце, которую они интерпретируют как утверждение о том, что аргументы имеют равные значения, другими словами, что функциональное значение составного выражения истинно . [ требуется ссылка ]
Логическое равенство — это операция над двумя логическими значениями , обычно значениями двух утверждений , которая возвращает значение «истина» тогда и только тогда, когда оба операнда ложны или оба операнда истинны.
Таблица истинности p EQ q ( также записывается как p = q , p ↔ q , Epq , p ≡ q или p == q ) выглядит следующим образом:
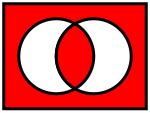
Форма ( x = y ) эквивалентна форме ( x ∧ y ) ∨ (¬ x ∧ ¬ y ).
Для операндов x и y таблица истинности оператора логического равенства выглядит следующим образом:
В математике знак плюс "+" почти всегда указывает на операцию, которая удовлетворяет аксиомам, назначенным для сложения в типе алгебраической структуры , известной как поле . Для булевой алгебры это означает, что логическая операция, обозначенная "+", не то же самое, что и инклюзивная дизъюнкция , обозначенная "∨", но на самом деле эквивалентна оператору логического неравенства, обозначенному "≠", или, что то же самое, исключающей дизъюнкции , обозначенной "XOR" или "⊕". Естественно, эти различия в использовании привели к некоторым сбоям в общении между математиками и инженерами-коммутаторами на протяжении многих лет. В любом случае, имеется следующий массив соответствующих форм для символов, связанных с логическим неравенством:
Это объясняет, почему «EQ» часто называют « XNOR » в комбинационной логике инженеров-схемотехников, поскольку это отрицание операции XOR ; «NXOR» — менее распространенная альтернатива. [1] Другое обоснование общепризнанно сложного названия «XNOR» заключается в том, что оно начинается с оператора NOR «оба ложны», а затем добавляется исключение «или оба истинны».