Принцип включения-исключения

Методика подсчета в комбинаторике

Диаграмма Венна, показывающая объединение множеств A и B как все, что не закрашено белым цветом

В комбинаторике принцип включения-исключения представляет собой метод подсчета, который обобщает известный метод получения числа элементов в объединении двух конечных множеств ; символически выражается как

${\displaystyle |A\cup B|=|A|+|B|-|A\cap B|}$

где A и B — два конечных множества, а | S | указывает мощность множества S (которую можно рассматривать как число элементов множества, если множество конечно ). Формула выражает тот факт, что сумма размеров двух множеств может быть слишком большой, поскольку некоторые элементы могут быть учтены дважды. Дважды учтенные элементы — это те, которые находятся на пересечении двух множеств, и подсчет корректируется путем вычитания размера пересечения.

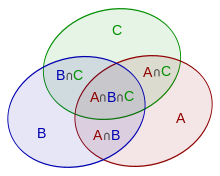
Принцип включения-исключения, являющийся обобщением случая двух множеств, возможно, более наглядно проявляется в случае трех множеств, который для множеств A , B и C задается выражением

${\displaystyle |A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|}$

Эту формулу можно проверить, подсчитав, сколько раз каждая область на диаграмме Венна включена в правую часть формулы. В этом случае при удалении вкладов пересчитанных элементов число элементов во взаимном пересечении трех множеств вычиталось слишком часто, поэтому его необходимо добавить обратно, чтобы получить правильную сумму.

Включение-исключение, проиллюстрированное диаграммой Венна для трех множеств

Обобщение результатов этих примеров дает принцип включения-исключения. Чтобы найти мощность объединения n множеств:

1. Укажите мощности множеств.
2. Исключить мощности попарных пересечений.
3. Включите мощности тройных пересечений.
4. Исключите мощности четверных пересечений.
5. Включите мощности пятеричных пересечений.
6. Продолжайте, пока мощность пересечения по n элементов не будет включена (если n нечетно) или исключена ( если n четно).

Название происходит от идеи, что принцип основан на чрезмерно щедром включении , за которым следует компенсирующее исключение . Эта концепция приписывается Аврааму де Муавуру (1718), ^[1] хотя впервые она появляется в статье Даниэля да Силвы (1854) ^[2] и позже в статье Дж. Дж. Сильвестра (1883). ^[3] Иногда принцип называют формулой да Силвы или Сильвестра из-за этих публикаций. Принцип можно рассматривать как пример метода решета, широко используемого в теории чисел , и иногда его называют формулой решета . ^[4]

Поскольку конечные вероятности вычисляются как подсчеты относительно мощности пространства вероятностей , формулы для принципа включения-исключения остаются действительными, когда мощности множеств заменяются конечными вероятностями. В более общем смысле, обе версии принципа можно поместить под общую зонтику теории меры .

В очень абстрактной постановке принцип включения-исключения может быть выражен как вычисление обратной матрицы определенной матрицы. ^[5] Эта обратная имеет особую структуру, что делает принцип чрезвычайно ценным методом в комбинаторике и смежных областях математики. Как выразился Джан-Карло Рота : ^[6]

«Одним из самых полезных принципов перечисления в дискретной теории вероятностей и комбинаторной теории является знаменитый принцип включения-исключения. При умелом применении этот принцип дал решение многих комбинаторных задач».

Формула

В своей общей формуле принцип включения-исключения утверждает, что для конечных множеств A ₁ , ..., A _n имеет место тождество

Каждый член формулы включения-исключения постепенно корректирует подсчет, пока, наконец, каждая часть диаграммы Венна не будет подсчитана ровно один раз.

Это можно компактно записать как

${\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=1}^{n}(-1)^{k+1}\left(\sum _{1\leqslant i_{1}<\cdots <i_{k}\leqslant n}|A_{i_{1}}\cap \cdots \cap A_{i_{k}}|\right)}$

или

${\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{\emptyset \neq J\subseteq \{1,\ldots ,n\}}(-1)^{|J|+1}\left|\bigcap _{j\in J}A_{j}\right|.}$

На словах, чтобы подсчитать количество элементов в конечном объединении конечных множеств, сначала суммируйте мощности отдельных множеств, затем вычтите количество элементов, которые появляются по крайней мере в двух множествах, затем прибавьте количество элементов, которые появляются по крайней мере в трех множествах, затем вычтите количество элементов, которые появляются по крайней мере в четырех множествах, и т. д. Этот процесс всегда заканчивается, поскольку не может быть элементов, которые появляются в большем количестве множеств в объединении. (Например, если не может быть элементов, которые появляются в более чем множествах; эквивалентно, не может быть элементов, которые появляются по крайней мере в множествах.) ${\displaystyle n=4,}$ ${\displaystyle 4}$ ${\displaystyle 5}$

В приложениях этот принцип часто можно увидеть выраженным в его дополнительной форме. То есть, если S — конечное универсальное множество , содержащее все A _i , и если обозначить дополнение A _i в S , то по законам Де Моргана мы имеем ${\displaystyle {\bar {A_{i}}}}$

${\displaystyle \left|\bigcap _{i=1}^{n}{\bar {A_{i}}}\right|=\left|S-\bigcup _{i=1}^{n}A_{i}\right|=|S|-\sum _{i=1}^{n}|A_{i}|+\sum _{1\leqslant i<j\leqslant n}|A_{i}\cap A_{j}|-\cdots +(-1)^{n}|A_{1}\cap \cdots \cap A_{n}|.}$

В качестве другого варианта утверждения, пусть P ₁ , ..., P _n будет списком свойств, которые элементы множества S могут или не могут иметь, тогда принцип включения-исключения предоставляет способ вычисления количества элементов S , которые не имеют ни одного из свойств. Просто пусть A _i будет подмножеством элементов S , которые имеют свойство P _{i ,} и используйте принцип в его дополнительной форме. Этот вариант принадлежит JJ Sylvester . ^[1]

Обратите внимание, что если вы примете во внимание только первые суммы m<n справа (в общей форме принципа), то вы получите завышенную оценку, если m нечетное, и заниженную оценку, если m четное.

Примеры

Подсчет расстройств

Более сложный пример следующий.

Предположим, что есть колода из n карт, пронумерованных от 1 до  n . Предположим, что карта с номером m находится в правильном положении, если это m ^-я карта в колоде. Сколькими способами, W , можно перетасовать карты, чтобы хотя бы 1 карта оказалась в правильном положении?

Начнем с определения множества A _m , которое представляет собой все упорядочения карточек с m- ^й карточкой, которая является правильной. Тогда число упорядочений, W , с хотя бы одной карточкой, находящейся в правильной позиции, m , равно

${\displaystyle W=\left|\bigcup _{m=1}^{n}A_{m}\right|.}$

Применить принцип включения-исключения,

${\displaystyle W=\sum _{m_{1}=1}^{n}|A_{m_{1}}|-\sum _{1\leqslant m_{1}<m_{2}\leqslant n}|A_{m_{1}}\cap A_{m_{2}}|+\cdots +(-1)^{p-1}\sum _{1\leqslant m_{1}<\cdots <m_{p}\leqslant n}|A_{m_{1}}\cap \cdots \cap A_{m_{p}}|+\cdots }$

Каждое значение представляет собой набор перетасовок, имеющих по крайней мере p значений m ₁ , ...,  m _p в правильной позиции. Обратите внимание, что количество перетасовок с по крайней мере p правильными значениями зависит только от p , а не от конкретных значений . Например, количество перетасовок, имеющих 1- ^ю , 3 ^-ю и 17 ^-ю карты в правильной позиции, равно количеству перетасовок, имеющих 2 ^-ю , 5 ^-ю и 13 ^-ю карты в правильной позиции. Имеет значение только то, что из n карт 3 были выбраны для правильной позиции. Таким образом, в p ^-й сумме (см. комбинацию ) есть равные члены . ${\displaystyle A_{m_{1}}\cap \cdots \cap A_{m_{p}}}$ ${\displaystyle m}$ ${\textstyle {n \choose p}}$

${\displaystyle W={n \choose 1}|A_{1}|-{n \choose 2}|A_{1}\cap A_{2}|+\cdots +(-1)^{p-1}{n \choose p}|A_{1}\cap \cdots \cap A_{p}|+\cdots }$

${\displaystyle |A_{1}\cap \cdots \cap A_{p}|}$— это число упорядочений, имеющих p элементов в правильном положении, которое равно числу способов упорядочения оставшихся n  −  p элементов, или ( n  −  p )!. Таким образом, мы в итоге получаем:

${\displaystyle {\begin{aligned}W&={n \choose 1}(n-1)!-{n \choose 2}(n-2)!+\cdots +(-1)^{p-1}{n \choose p}(n-p)!+\cdots \\&=\sum _{p=1}^{n}(-1)^{p-1}{n \choose p}(n-p)!\\&=\sum _{p=1}^{n}(-1)^{p-1}{\frac {n!}{p!(n-p)!}}(n-p)!\\&=\sum _{p=1}^{n}(-1)^{p-1}{\frac {n!}{p!}}\end{aligned}}}$

Перестановка, в которой ни одна карта не находится в правильном положении, называется расстройством . Принимая n ! за общее число перестановок, вероятность Q того, что случайная перестановка приведет к расстройству, определяется как

${\displaystyle Q=1-{\frac {W}{n!}}=\sum _{p=0}^{n}{\frac {(-1)^{p}}{p!}},}$

усечение до n  + 1 членов разложения Тейлора e −1 ^. Таким образом, вероятность угадать порядок перетасованной колоды карт и ошибиться относительно каждой карты составляет приблизительно e ⁻¹ или 37%.

Особый случай

Ситуация, которая появляется в приведенном выше примере расстройства, встречается достаточно часто, чтобы заслуживать особого внимания. ^[7] А именно, когда размер множеств пересечения, появляющихся в формулах для принципа включения-исключения, зависит только от количества множеств в пересечениях, а не от того, какие множества появляются. Более формально, если пересечение

${\displaystyle A_{J}:=\bigcap _{j\in J}A_{j}}$

имеет одинаковую мощность, скажем, α _k = | A _J |, для каждого k -элементного подмножества J из {1, ...,  n }, тогда

${\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}\alpha _{k}.}$

Или, в дополнительной форме, где универсальное множество S имеет мощность α ₀ ,

${\displaystyle \left|S\smallsetminus \bigcup _{i=1}^{n}A_{i}\right|=\alpha _{0}-\sum _{k=0}^{n}(-1)^{k-1}{\binom {n}{k}}\alpha _{k}.}$

Формула обобщения

При наличии семейства (повторения допускаются) подмножеств A ₁ , A ₂ , ..., A _n универсального множества S принцип включения-исключения вычисляет количество элементов S ни в одном из этих подмножеств. Обобщение этой концепции вычислило бы количество элементов S , которые появляются ровно в некотором фиксированном m из этих множеств.

Пусть N = [ n ] = {1,2,..., n }. Если мы определим , то принцип включения-исключения можно записать так, используя обозначения предыдущего раздела; число элементов S , не содержащихся ни в одном из A _{i ,} равно: ${\displaystyle A_{\emptyset }=S}$

${\displaystyle \sum _{J\subseteq [n]}(-1)^{|J|}|A_{J}|.}$

Если I — фиксированное подмножество индексного множества N , то число элементов, которые принадлежат A _i для всех i из I и ни для каких других значений, равно: ^[8]

${\displaystyle \sum _{I\subseteq J}(-1)^{|J|-|I|}|A_{J}|.}$

Определим множества

${\displaystyle B_{k}=A_{I\cup \{k\}}{\text{ for }}k\in N\smallsetminus I.}$

Мы ищем число элементов, не содержащихся ни в одном из B _k , которое по принципу включения-исключения (с ), равно ${\displaystyle B_{\emptyset }=A_{I}}$

${\displaystyle \sum _{K\subseteq N\smallsetminus I}(-1)^{|K|}|B_{K}|.}$

Соответствие K ↔ J = I ∪ K между подмножествами N  \  I и подмножествами N , содержащими I, является биекцией, и если J и K соответствуют при этом отображении, то B _K = A _J , что показывает, что результат верен.

По вероятности

В теории вероятности для событий A ₁ , ..., A _n в вероятностном пространстве принцип включения-исключения принимает вид для n  = 2 ${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}$

${\displaystyle \mathbb {P} (A_{1}\cup A_{2})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})-\mathbb {P} (A_{1}\cap A_{2}),}$

для n  = 3

${\displaystyle \mathbb {P} (A_{1}\cup A_{2}\cup A_{3})=\mathbb {P} (A_{1})+\mathbb {P} (A_{2})+\mathbb {P} (A_{3})-\mathbb {P} (A_{1}\cap A_{2})-\mathbb {P} (A_{1}\cap A_{3})-\mathbb {P} (A_{2}\cap A_{3})+\mathbb {P} (A_{1}\cap A_{2}\cap A_{3})}$

и вообще

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=\sum _{i=1}^{n}\mathbb {P} (A_{i})-\sum _{i<j}\mathbb {P} (A_{i}\cap A_{j})+\sum _{i<j<k}\mathbb {P} (A_{i}\cap A_{j}\cap A_{k})+\cdots +(-1)^{n-1}\sum _{i<...<n}\mathbb {P} \left(\bigcap _{i=1}^{n}A_{i}\right),}$

что можно записать в замкнутом виде как

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=\sum _{k=1}^{n}\left((-1)^{k-1}\sum _{I\subseteq \{1,\ldots ,n\} \atop |I|=k}\mathbb {P} (A_{I})\right),}$

где последняя сумма пробегает все подмножества I индексов 1, ..., n, которые содержат ровно k элементов, и

${\displaystyle A_{I}:=\bigcap _{i\in I}A_{i}}$

обозначает пересечение всех A _i с индексом в I .

Согласно неравенствам Бонферрони , сумма первых членов формулы является попеременно верхней и нижней границей для LHS . Это можно использовать в случаях, когда полная формула слишком громоздка.

Для общего пространства с мерой ₍ S , Σ, μ ) и измеримых подмножеств A1 , ..., An конечной меры указанные выше тождества также справедливы, когда вероятностная мера _{заменяется} мерой μ . ${\displaystyle \mathbb {P} }$

Особый случай

Если в вероятностной версии принципа включения-исключения вероятность пересечения A _I зависит только от мощности I , что означает, что для каждого k из {1, ...,  n } существует a _k такое, что

${\displaystyle a_{k}=\mathbb {P} (A_{I}){\text{ for every }}I\subset \{1,\ldots ,n\}{\text{ with }}|I|=k,}$

тогда приведенная выше формула упрощается до

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=\sum _{k=1}^{n}(-1)^{k-1}{\binom {n}{k}}a_{k}}$

из-за комбинаторной интерпретации биномиального коэффициента . Например, если события независимы и одинаково распределены , то для всех i , и мы имеем , в этом случае выражение выше упрощается до ${\textstyle {\binom {n}{k}}}$ ${\displaystyle A_{i}}$ ${\displaystyle \mathbb {P} (A_{i})=p}$ ${\displaystyle a_{k}=p^{k}}$

${\displaystyle \mathbb {P} \left(\bigcup _{i=1}^{n}A_{i}\right)=1-(1-p)^{n}.}$

(Этот результат можно также получить более просто, рассмотрев пересечение дополнений событий .) ${\displaystyle A_{i}}$

Аналогичное упрощение возможно в случае общего мерного пространства и измеримых подмножеств конечной меры. ${\displaystyle (S,\Sigma ,\mu )}$ ${\displaystyle A_{1},\dots ,A_{n}}$

Есть еще одна формула, используемая в точечных процессах . Пусть будет конечным множеством и будет случайным подмножеством . Пусть будет любым подмножеством , тогда ${\displaystyle S}$ ${\displaystyle P}$ ${\displaystyle S}$ ${\displaystyle A}$ ${\displaystyle S}$

$${\displaystyle {\begin{aligned}\mathbb {P} (P=A)&=\mathbb {P} (P\supset A)-\sum _{j_{1}\in S\setminus A}\mathbb {P} (P\supset A\cup {j_{1}})\\&+\sum _{j_{1},j_{2}\in S\setminus A\ j_{1}\neq j_{2}}\mathbb {P} (P\supset A\cup {j_{1},j_{2}})+\dots \\&+(-1)^{|S|-|A|}\mathbb {P} (P\supset S)\\&=\sum _{A\subset J\subset S}(-1)^{|J|-|A|}\mathbb {P} (P\supset J).\end{aligned}}}$$

Другие формулы

Этот принцип иногда формулируется в форме ^[9], которая гласит, что если

${\displaystyle g(A)=\sum _{S\subseteq A}f(S)}$

затем

Комбинаторная и вероятностная версии принципа включения-исключения являются примерами ( 2 ).

Доказательство

Возьми , , и ${\displaystyle {\underline {m}}=\{1,2,\ldots ,m\}}$ ${\displaystyle f({\underline {m}})=0}$

${\displaystyle f(S)=\left|\bigcap _{i\in {\underline {m}}\smallsetminus S}A_{i}\smallsetminus \bigcup _{i\in S}A_{i}\right|{\text{ and }}f(S)=\mathbb {P} \left(\bigcap _{i\in {\underline {m}}\smallsetminus S}A_{i}\smallsetminus \bigcup _{i\in S}A_{i}\right)}$

соответственно для всех наборов с . Тогда получаем ${\displaystyle S}$ ${\displaystyle S\subsetneq {\underline {m}}}$

${\displaystyle g(A)=\left|\bigcap _{i\in {\underline {m}}\smallsetminus A}A_{i}\right|,\quad g({\underline {m}})=\left|\bigcup _{i\in {\underline {m}}}A_{i}\right|{\text{ and }}g(A)=\mathbb {P} \left(\bigcap _{i\in {\underline {m}}\smallsetminus A}A_{i}\right),~~g({\underline {m}})=\mathbb {P} \left(\bigcup _{i\in {\underline {m}}}A_{i}\right)}$

соответственно для всех множеств с . Это происходит потому, что элементы из могут также содержаться в других ( с ), и -формула проходит точно через все возможные расширения множеств с другими , считая только для множества, которое соответствует поведению членства , если проходит через все подмножества (как в определении ). ${\displaystyle A}$ ${\displaystyle A\subsetneq {\underline {m}}}$ ${\displaystyle a}$ ${\displaystyle \cap _{i\in {\underline {m}}\smallsetminus A}A_{i}}$ ${\displaystyle A_{i}}$ ${\displaystyle A_{i}}$ ${\displaystyle i\in A}$ ${\displaystyle \cap \smallsetminus \cup }$ ${\displaystyle \{A_{i}\mid i\in {\underline {m}}\smallsetminus A\}}$ ${\displaystyle A_{i}}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle S}$ ${\displaystyle A}$ ${\displaystyle g(A)}$

Так как , то из ( 2 ) получаем при этом ${\displaystyle f({\underline {m}})=0}$ ${\displaystyle A={\underline {m}}}$

${\displaystyle \sum _{{\underline {m}}\supseteq T\supsetneq \varnothing }(-1)^{|T|-1}g({\underline {m}}\smallsetminus T)=\sum _{\varnothing \subseteq S\subsetneq {\underline {m}}}(-1)^{m-|S|-1}g(S)=g({\underline {m}})}$

и при перестановке сторон получаются комбинаторная и вероятностная версии принципа включения-исключения.

Если рассматривать число как набор его простых множителей, то ( 2 ) является обобщением формулы обращения Мёбиуса для натуральных чисел без квадратов . Таким образом, ( 2 ) рассматривается как формула обращения Мёбиуса для алгебры инцидентности частично упорядоченного множества всех подмножеств A. ${\displaystyle n}$

Для обобщения полной версии формулы обращения Мёбиуса ( 2 ) необходимо обобщить на мультимножества . Для мультимножеств вместо множеств ( 2 ) становится

где мультимножество, для которого , и ${\displaystyle A-S}$ ${\displaystyle (A-S)\uplus S=A}$

• μ ( S ) = 1, если S является множеством (т.е. мультимножеством без двойных элементов) четной мощности .
• μ ( S ) = −1, если S является множеством (т.е. мультимножеством без двойных элементов) нечетной мощности.
• μ ( S ) = 0, если S является правильным мультимножеством (т.е. S имеет двойные элементы).

Обратите внимание, что это просто из ( 2 ) в случае, если это множество. ${\displaystyle \mu (A-S)}$ ${\displaystyle (-1)^{|A|-|S|}}$ ${\displaystyle A-S}$

Доказательство ( 3 )

Подставим в правую часть ( 3 ). Обратите внимание, что появляется один раз с обеих сторон ( 3 ). Поэтому мы должны показать, что для всех с , члены в правой части ( 3 ) сокращаются. Для этого возьмем фиксированное значение , такое что , и возьмем произвольное фиксированное значение , такое что . $${\displaystyle g(S)=\sum _{T\subseteq S}f(T)}$$ ${\displaystyle f(A)}$ ${\displaystyle T}$ ${\displaystyle T\subsetneq A}$ ${\displaystyle f(T)}$ ${\displaystyle T}$ ${\displaystyle T\subsetneq A}$ ${\displaystyle a\in A}$ ${\displaystyle a\notin T}$

Обратите внимание, что должен быть набор для каждого положительного или отрицательного появления в правой части ( 3 ), который получается посредством мультимножества, такого что . Теперь каждое появление в правой части ( 3 ), которое получается посредством такого что является набором, который содержит , сокращается с тем, который получается посредством соответствующего такого что является набором, который не содержит . Это дает желаемый результат. ${\displaystyle A-S}$ ${\displaystyle f(T)}$ ${\displaystyle S}$ ${\displaystyle T\subseteq S\subseteq A}$ ${\displaystyle f(T)}$ ${\displaystyle S}$ ${\displaystyle A-S}$ ${\displaystyle a}$ ${\displaystyle S}$ ${\displaystyle A-S}$ ${\displaystyle a}$

Приложения

Принцип включения-исключения широко используется, и здесь можно упомянуть лишь некоторые из его применений.

Подсчет расстройств

Хорошо известное применение принципа включения–исключения — это комбинаторная задача подсчета всех расстройств конечного множества. Расстройство множества A — это биекция из A в себя, не имеющая неподвижных точек. С помощью принципа включения–исключения можно показать, что если мощность A равна n , то количество расстройств равно [ n !/  e ], где [ x ] обозначает ближайшее целое число к x ; подробное доказательство доступно здесь , а также см. раздел примеров выше.

Впервые задача подсчета количества сбоев встречается в ранней книге об азартных играх: Essai d'analyse sur les jeux de hazard, написанной П. Р. де Монмором (1678 – 1719), и была известна как «задача Монмора» или по названию, которое он ей дал, « problème des rencontres ». ^[10] Задача также известна как задача о шляпе.

Число нарушений также известно как субфакториал n , который записывается как ! n . Из этого следует, что если всем биекциям приписана одинаковая вероятность, то вероятность того, что случайная биекция является нарушением, быстро приближается к 1/ e по мере роста n .

Подсчет перекрестков

Принцип включения-исключения, объединенный с законом Де Моргана , может быть использован для подсчета мощности пересечения множеств. Пусть представим дополнение A _k относительно некоторого универсального множества A такого, что для каждого k . Тогда мы имеем ${\displaystyle {\overline {A_{k}}}}$ ${\displaystyle A_{k}\subseteq A}$

${\displaystyle \bigcap _{i=1}^{n}A_{i}={\overline {\bigcup _{i=1}^{n}{\overline {A_{i}}}}}}$

тем самым превращая задачу поиска пересечения в задачу поиска объединения.

Раскраска графа

Принцип включения-исключения лежит в основе алгоритмов для ряда NP-трудных задач разбиения графов, таких как раскраска графов. ^[11]

Хорошо известным применением принципа является построение хроматического многочлена графа. ^[12]

Совершенные паросочетания двудольного графа

Число идеальных паросочетаний двудольного графа можно вычислить, используя принцип. ^[13]

Количество функций on

При заданных конечных множествах A и B , сколько сюръективных функций (функций на) существует из A в B ? Без потери общности мы можем взять A = {1, ..., k } и B = {1, ..., n }, поскольку важны только мощности множеств. Используя S как множество всех функций из A в B и определяя для каждого i в B свойство P _i как «функция пропускает элемент i в B » ( i не находится в образе функции), принцип включения–исключения дает число функций на между A и B как: ^[14]

${\displaystyle \sum _{j=0}^{n}{\binom {n}{j}}(-1)^{j}(n-j)^{k}.}$

Перестановки с запрещенными позициями

Перестановка множества S = {1, ..., n } , в которой каждый элемент S ограничен тем, что не может находиться в определенных позициях (здесь перестановка рассматривается как упорядочение элементов S ), называется перестановкой с запрещенными позициями . Например, при S = ​​{1,2,3,4} перестановки с ограничением, что элемент 1 не может находиться в позициях 1 или 3, а элемент 2 не может находиться в позиции 4, следующие: 2134, 2143, 3124, 4123, 2341, 2431, 3241, 3421, 4231 и 4321. Позволяя A _i быть множеством позиций, в которых элемент i не может находиться, а свойству P _i быть свойством, что перестановка помещает элемент i в позицию в A _i , принцип включения-исключения может быть использован для подсчета количества перестановок, которые удовлетворяют всем ограничениям. ^[15]

В данном примере имеется 12 = 2(3!) перестановок со свойством P ₁ , 6 = 3! перестановок со свойством P ₂ и ни одна перестановка не имеет свойств P ₃ или P ₄ , так как для этих двух элементов нет ограничений. Количество перестановок, удовлетворяющих ограничениям, таким образом:

4! − (12 + 6 + 0 + 0) + (4) = 24 − 18 + 4 = 10.

Последняя 4 в этом вычислении — это число перестановок, имеющих оба свойства P ₁ и P _2. Других ненулевых вкладов в формулу нет.

Числа Стерлинга второго рода

Числа Стирлинга второго рода , S ( n , k ) подсчитывают количество разбиений множества из n элементов на k непустых подмножеств (неразличимых ящиков ). Явную формулу для них можно получить, применив принцип включения–исключения к очень близкой задаче, а именно, подсчету количества разбиений n -множества на k непустых, но различимых ящиков ( упорядоченных непустых подмножеств). Используя универсальное множество, состоящее из всех разбиений n -множества на k (возможно, пустых) различимых ящиков, A ₁ , A ₂ , ..., A _k , и свойства P _i , означающие, что в разбиении ящик A _i пустой, принцип включения–исключения дает ответ на связанный результат. Деление на k ! для удаления искусственного упорядочения дает число Стирлинга второго рода: ^[16]

${\displaystyle S(n,k)={\frac {1}{k!}}\sum _{t=0}^{k}(-1)^{t}{\binom {k}{t}}(k-t)^{n}.}$

Ладейные многочлены

Ладейный полином — это производящая функция числа способов размещения неатакующих ладей на доске B , которая выглядит как подмножество клеток шахматной доски ; то есть никакие две ладьи не могут находиться в одном ряду или столбце. Доска B — это любое подмножество клеток прямоугольной доски с n строками и m столбцами; мы думаем о ней как о клетках, в которые разрешено поставить ладью. Коэффициент r k ₍ B ) от x ^k в ладейном полиноме R _B ( x ) — это число способов, которыми k ладей, ни одна из которых не атакует другую, могут быть расставлены в клетках B . Для любой доски B существует дополнительная доска, состоящая из клеток прямоугольной доски, которые не находятся в B . Эта дополнительная доска также имеет ладейный полином с коэффициентами ${\displaystyle B'}$ ${\displaystyle R_{B'}(x)}$ ${\displaystyle r_{k}(B').}$

Иногда удобно иметь возможность вычислить наивысший коэффициент ладейного полинома через коэффициенты ладейного полинома дополнительной доски. Без потери общности можно предположить, что n ≤ m , так что этот коэффициент равен r _n ( B ). Количество способов разместить n неатакующих ладей на полной n × m "шахматной доске" (без учета того, размещены ли ладьи в клетках доски B ) определяется падающим факториалом :

${\displaystyle (m)_{n}=m(m-1)(m-2)\cdots (m-n+1).}$

Пусть P _i — свойство, что при размещении n неатакующих ладей на полной доске в столбце i есть ладья , которая не находится ни в одной клетке доски B , тогда по принципу включения-исключения имеем: ^[17]

${\displaystyle r_{n}(B)=\sum _{t=0}^{n}(-1)^{t}(m-t)_{n-t}r_{t}(B').}$

Фи-функция Эйлера

Тотиент Эйлера или фи-функция, φ ( n ) — это арифметическая функция , которая подсчитывает количество положительных целых чисел, меньших или равных n , которые взаимно просты с n . То есть, если n — положительное целое число , то φ( n ) — это количество целых чисел k в диапазоне 1 ≤ k ≤ n , которые не имеют общего множителя с n , кроме 1. Принцип включения-исключения используется для получения формулы для φ( n ). Пусть S — множество {1, ..., n } и определите свойство P _i как то, что число из S делится на простое число p _i , для 1 ≤ i ≤ r , где разложение на простые множители

${\displaystyle n=p_{1}^{a_{1}}p_{2}^{a_{2}}\cdots p_{r}^{a_{r}}.}$

Затем, ^[18]

${\displaystyle \varphi (n)=n-\sum _{i=1}^{r}{\frac {n}{p_{i}}}+\sum _{1\leqslant i<j\leqslant r}{\frac {n}{p_{i}p_{j}}}-\cdots =n\prod _{i=1}^{r}\left(1-{\frac {1}{p_{i}}}\right).}$

Метод гиперболы Дирихле

Пример метода гиперболы Дирихле с и ${\displaystyle n=10,}$ ${\displaystyle a\approx 2.7,}$ ${\displaystyle b\approx 3.7.}$

Метод гиперболы Дирихле повторно выражает сумму мультипликативной функции путем выбора подходящей свертки Дирихле , признавая, что сумма ${\displaystyle f(n)}$ ${\displaystyle f=g\ast h}$

${\displaystyle F(n)=\sum _{k=1}^{n}f(k)=\sum _{k=1}^{n}\sum _{xy=k}^{}g(x)h(y)}$

можно переформулировать как сумму по точкам решетки в области, ограниченной , и , разделив эту область на две перекрывающиеся подобласти и, наконец, используя принцип включения-исключения, сделать вывод, что ${\displaystyle x\geq 1}$ ${\displaystyle y\geq 1}$ ${\displaystyle xy\leq n}$

${\displaystyle F(n)=\sum _{k=1}^{n}f(k)=\sum _{k=1}^{n}\sum _{xy=k}^{}g(x)h(y)=\sum _{x=1}^{a}\sum _{y=1}^{n/x}g(x)h(y)+\sum _{y=1}^{b}\sum _{x=1}^{n/y}g(x)h(y)-\sum _{x=1}^{a}\sum _{y=1}^{b}g(x)h(y).}$

Разбавленный принцип включения-исключения

Во многих случаях, когда принцип мог бы дать точную формулу (в частности, подсчет простых чисел с использованием решета Эратосфена ), возникающая формула не предлагает полезного содержания, поскольку количество членов в ней чрезмерно. Если каждый член в отдельности может быть оценен точно, накопление ошибок может означать, что формула включения-исключения не применима напрямую. В теории чисел эта трудность была рассмотрена Вигго Бруном . После медленного старта его идеи были подхвачены другими, и было разработано большое количество методов решета . Они, например, могут попытаться найти верхние границы для «просеянных» множеств, а не точную формулу.

Пусть A ₁ , ..., A _n — произвольные множества и p ₁ , ..., p _{n —} действительные числа в замкнутом единичном интервале [0, 1] . Тогда для каждого четного числа k из {0, ..., n } индикаторные функции удовлетворяют неравенству: ^[19]

${\displaystyle 1_{A_{1}\cup \cdots \cup A_{n}}\geq \sum _{j=1}^{k}(-1)^{j-1}\sum _{1\leq i_{1}<\cdots <i_{j}\leq n}p_{i_{1}}\dots p_{i_{j}}\,1_{A_{i_{1}}\cap \cdots \cap A_{i_{j}}}.}$

Доказательство основного утверждения

Выберите элемент, содержащийся в объединении всех множеств, и пусть будут отдельными множествами, содержащими его. (Обратите внимание, что t > 0.) Поскольку элемент учитывается ровно один раз левой частью уравнения ( 1 ), нам нужно показать, что он учитывается ровно один раз правой частью. С правой стороны единственные ненулевые вклады возникают, когда все подмножества в определенном члене содержат выбранный элемент, то есть все подмножества выбираются из . Вклад равен единице для каждого из этих множеств (плюс или минус в зависимости от члена) и, следовательно, является просто (знаковым) числом этих подмножеств, используемых в члене. Тогда мы имеем: ${\displaystyle A_{1},A_{2},\dots ,A_{t}}$ ${\displaystyle A_{1},A_{2},\dots ,A_{t}}$

${\displaystyle {\begin{aligned}|\{A_{i}\mid 1\leqslant i\leqslant t\}|&-|\{A_{i}\cap A_{j}\mid 1\leqslant i<j\leqslant t\}|+\cdots +(-1)^{t+1}|\{A_{1}\cap A_{2}\cap \cdots \cap A_{t}\}|={\binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}}.\end{aligned}}}$

По биномиальной теореме ,

${\displaystyle 0=(1-1)^{t}={\binom {t}{0}}-{\binom {t}{1}}+{\binom {t}{2}}-\cdots +(-1)^{t}{\binom {t}{t}}.}$

Используя тот факт, что и переставляя члены, имеем ${\displaystyle {\binom {t}{0}}=1}$

${\displaystyle 1={\binom {t}{1}}-{\binom {t}{2}}+\cdots +(-1)^{t+1}{\binom {t}{t}},}$

и поэтому выбранный элемент учитывается только один раз в правой части уравнения ( 1 ).

Алгебраическое доказательство

Алгебраическое доказательство может быть получено с использованием индикаторных функций (также известных как характеристические функции). Индикаторная функция подмножества S множества X — это функция

${\displaystyle {\begin{aligned}&\mathbf {1} _{S}:X\to \{0,1\}\\&\mathbf {1} _{S}(x)={\begin{cases}1&x\in S\\0&x\notin S\end{cases}}\end{aligned}}}$

Если и являются двумя подмножествами , то ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle X}$

${\displaystyle \mathbf {1} _{A}\cdot \mathbf {1} _{B}=\mathbf {1} _{A\cap B}.}$

Пусть A обозначает объединение множеств A ₁ , ..., A _n . Чтобы доказать принцип включения–исключения в общем виде, сначала проверим тождество ${\textstyle \bigcup _{i=1}^{n}A_{i}}$

для индикаторных функций, где:

${\displaystyle A_{I}=\bigcap _{i\in I}A_{i}.}$

Следующая функция

${\displaystyle \left(\mathbf {1} _{A}-\mathbf {1} _{A_{1}}\right)\left(\mathbf {1} _{A}-\mathbf {1} _{A_{2}}\right)\cdots \left(\mathbf {1} _{A}-\mathbf {1} _{A_{n}}\right)=0,}$

тождественно равен нулю, потому что: если x не принадлежит A , то все множители равны 0−0 = 0; и в противном случае, если x принадлежит некоторому A _m , то соответствующий m ^-й множитель равен 1−1=0. Раскрывая произведение в левой части, получаем уравнение ( 4 ).

Чтобы доказать принцип включения-исключения для мощности множеств, просуммируйте уравнение ( 4 ) по всем x в объединении A ₁ , ..., A _n . Чтобы вывести версию, используемую в вероятности, возьмите ожидание в ( 4 ). В общем случае, проинтегрируйте уравнение ( 4 ) относительно  μ . Всегда используйте линейность в этих выводах.

Смотрите также

• Неравенство Буля  – Неравенство, применяемое к вероятностным пространствам
• Комбинаторные принципы  – Методы, используемые в комбинаторике
• Тождество максимума-минимума  – связывает максимальный элемент множества чисел и минимумы его непустых подмножеств.
• Проблема с ожерельем
• Принцип ящика  — если предметов больше, чем коробок, в которых они хранятся, в одной коробке должно быть не менее двух предметов.
• Формула Шютте–Несбитта  – математическая формула в теории вероятностейPages displaying wikidata descriptions as a fallback

Примечания

1. Roberts & Tesman 2009, стр. 405
2. Мазур 2010, стр. 94
3. ван Линт и Уилсон 1992, стр. 77
4. ван Линт и Уилсон 1992, стр. 77
5. Стэнли 1986, стр. 64
6. Рота, Джан-Карло (1964), «Об основах комбинаторной теории I. Теория функций Мёбиуса», Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete , 2 (4): 340–368, doi : 10.1007/BF00531932 , S2CID  121334025
7. Бруальди 2010, стр. 167–168
8. Кэмерон 1994, стр. 78
9. Грэм, Гретшель и Ловас 1995, стр. 1049
10. ван Линт и Уилсон 1992, стр. 77-8.
11. Бьорклунд, Хусфельдт и Койвисто, 2009 г.
12. Гросс 2008, стр. 211–213
13. Гросс 2008, стр. 208–10
14. Мазур 2010, стр.84-5, 90
15. Бруальди 2010, стр. 177–81
16. Бруальди 2010, стр. 282–287
17. Робертс и Тесман, 2009, стр. 419–20.
18. ван Линт и Уилсон 1992, стр. 73
19. (Фернандес, Фрелих и Алан Д. 1992, предложение 12.6)

Ссылки

• Алленби, RBJT; Сломсон, Алан (2010), Как считать: Введение в комбинаторику, дискретную математику и ее приложения (2-е изд.), CRC Press, стр. 51–60, ISBN 9781420082609
• Бьёрклунд, А.; Хусфельдт, Т.; Койвисто, М. (2009), «Разбиение множеств с помощью включения–исключения», SIAM Journal on Computing , 39 (2): 546–563, CiteSeerX  10.1.1.526.9573 , doi : 10.1137/070683933
• Бруальди, Ричард А. (2010), Введение в комбинаторику (5-е изд.), Prentice–Hall, ISBN 9780136020400
• Кэмерон, Питер Дж. (1994), Комбинаторика: темы, методы, алгоритмы , Cambridge University Press, ISBN 0-521-45761-0
• Фернандес, Роберто; Фрёлих, Юрг ; Алан Д., Сокал (1992), Случайные блуждания, критические явления и тривиальность в квантовой теории поля , Тексты и монографии по физике, Берлин: Springer-Verlag , стр. xviii+444, ISBN 3-540-54358-9, MR  1219313, Zbl  0761.60061
• Грэм, РЛ; Гретшель, М .; Ловас, Л. (1995), Справочник по комбинаторике (том 2) , MIT Press – North Holland, ISBN 9780262071710
• Гросс, Джонатан Л. (2008), Комбинаторные методы с компьютерными приложениями , Chapman&Hall/CRC, ISBN 9781584887430
• «Принцип включения и исключения», Энциклопедия математики , EMS Press , 2001 [1994]
• Мазур, Дэвид Р. (2010), Комбинаторика. Экскурсия , Математическая ассоциация Америки, ISBN 9780883857625
• Робертс, Фред С.; Тесман, Барри (2009), Прикладная комбинаторика (2-е изд.), CRC Press, ISBN 9781420099829
• Стэнли, Ричард П. (1986), Перечислительная комбинаторика, том I , Wadsworth & Brooks/Cole, ISBN 0534065465
• ван Линт, Дж. Х.; Уилсон, Р. М. (1992), Курс комбинаторики , Cambridge University Press, ISBN 0521422604

В данной статье использованы материалы, основанные на принципе включения-исключения из PlanetMath , лицензированные по лицензии Creative Commons Attribution/Share-Alike License .