Разница в различиях

Статистический метод использования данных наблюдений для причинного анализа

Разница в различиях ( DID ^[1] или DD ^[2] ) — это статистический метод , используемый в эконометрике и количественных исследованиях в социальных науках, который пытается имитировать экспериментальный исследовательский дизайн с использованием данных наблюдательного исследования , изучая дифференциальный эффект лечения на «группу лечения» по сравнению с « контрольной группой » в естественном эксперименте . ^[3] Он вычисляет эффект лечения (т. е. объясняющей переменной или независимой переменной ) на результат (т. е. ответной переменной или зависимой переменной ) путем сравнения среднего изменения с течением времени в переменной результата для группы лечения со средним изменением с течением времени для контрольной группы. Хотя он предназначен для смягчения эффектов посторонних факторов и смещения отбора , в зависимости от того, как выбрана группа лечения, этот метод все еще может быть подвержен определенным смещениям (например, средней регрессии , обратной причинности и смещению пропущенной переменной ).

В отличие от оценки временного ряда эффекта лечения у субъектов (которая анализирует различия с течением времени) или поперечной оценки эффекта лечения (которая измеряет разницу между группами лечения и контроля), разница в различиях использует панельные данные для измерения различий между группами лечения и контроля в изменениях в переменной результата, которые происходят с течением времени.

Общее определение

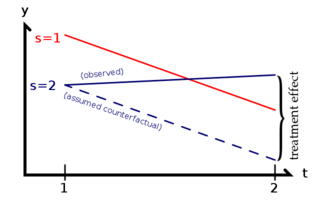
Разница в различиях требует данных, измеренных в группе лечения и контрольной группе в два или более различных периода времени, а именно, по крайней мере один период времени до «лечения» и по крайней мере один период времени после «лечения». В представленном примере результат в группе лечения представлен линией P, а результат в контрольной группе представлен линией S. Переменная результата (зависимая) в обеих группах измеряется в момент времени 1, до того, как любая из групп получила лечение (т. е. независимая или объясняющая переменная), представленная точками P ₁ и S ₁ . Затем группа лечения получает или испытывает лечение, и обе группы снова измеряются в момент времени 2. Не все различия между группами лечения и контроля в момент времени 2 (то есть, разница между P ₂ и S ₂ ) можно объяснить как эффект лечения, поскольку группа лечения и контрольная группа не начинали в одной и той же точке в момент времени 1. Таким образом, DID вычисляет «нормальную» разницу в переменной результата между двумя группами (разницу, которая все еще существовала бы, если бы ни одна из групп не испытывала лечение), представленную пунктирной линией Q . (Обратите внимание, что наклон от P ₁ к Q такой же, как наклон от S ₁ к S ₂ .) Эффект лечения — это разница между наблюдаемым результатом (P ₂ ) и «нормальным» результатом (разница между P ₂ и Q).

Формальное определение

Рассмотрим модель

${\displaystyle y_{it}~=~\gamma _{s(i)}+\lambda _{t}+\delta I(\dots )+\varepsilon _{it}}$

где — зависимая переменная для индивидуума и времени , — группа, к которой принадлежит (т. е. группа лечения или контрольная группа), а — сокращение для фиктивной переменной, равной 1, когда событие, описанное в , истинно, и 0 в противном случае. На графике зависимости времени от группы — вертикальный отсекаемый элемент для графика , а — временной тренд, общий для обеих групп в соответствии с предположением о параллельном тренде (см. предположения ниже). — эффект лечения, а — остаточный член . ${\displaystyle y_{it}}$ ${\displaystyle i}$ ${\displaystyle t}$ ${\displaystyle s(i)}$ ${\displaystyle i}$ ${\displaystyle I(\dots )}$ ${\displaystyle (\dots )}$ ${\displaystyle Y}$ ${\displaystyle \gamma _{s}}$ ${\displaystyle s}$ ${\displaystyle \lambda _{t}}$ ${\displaystyle \delta }$ ${\displaystyle \varepsilon _{it}}$

Рассмотрим среднее значение зависимой переменной и фиктивных показателей по группам и времени:

${\displaystyle {\begin{aligned}n_{s}&={\text{ number of individuals in group }}s\\{\overline {y}}_{st}&={\frac {1}{n_{s}}}\sum _{i=1}^{n}y_{it}\ I(s(i)~=~s),\\{\overline {\gamma }}_{s}&={\frac {1}{n_{s}}}\sum _{i=1}^{n}\gamma _{s(i)}\ I(s(i)~=~s)~=~\gamma _{s},\\{\overline {\lambda }}_{st}&={\frac {1}{n_{s}}}\sum _{i=1}^{n}\lambda _{t}\ I(s(i)~=~s)~=~\lambda _{t},\\D_{st}&={\frac {1}{n_{s}}}\sum _{i=1}^{n}I(s(i)~=~{\text{ treatment, }}t{\text{ in after period}})\ I(s(i)~=~s)~=~I(s~=~{\text{ treatment, }}t{\text{ in after period}}),\\{\overline {\varepsilon }}_{st}&={\frac {1}{n_{s}}}\sum _{i=1}^{n}\varepsilon _{it}\ I(s(i)~=~s),\end{aligned}}}$

и предположим для простоты, что и . Обратите внимание, что это не случайно; это просто кодирует, как маркируются группы и периоды. Тогда ${\displaystyle s=1,2}$ ${\displaystyle t=1,2}$ ${\displaystyle D_{st}}$

${\displaystyle {\begin{aligned}&({\overline {y}}_{11}-{\overline {y}}_{12})-({\overline {y}}_{21}-{\overline {y}}_{22})\\[6pt]={}&{\big [}(\gamma _{1}+\lambda _{1}+\delta D_{11}+{\overline {\varepsilon }}_{11})-(\gamma _{1}+\lambda _{2}+\delta D_{12}+{\overline {\varepsilon }}_{12}){\big ]}\\&\qquad {}-{\big [}(\gamma _{2}+\lambda _{1}+\delta D_{21}+{\overline {\varepsilon }}_{21})-(\gamma _{2}+\lambda _{2}+\delta D_{22}+{\overline {\varepsilon }}_{22}){\big ]}\\[6pt]={}&\delta (D_{11}-D_{12})+\delta (D_{22}-D_{21})+{\overline {\varepsilon }}_{11}-{\overline {\varepsilon }}_{12}+{\overline {\varepsilon }}_{22}-{\overline {\varepsilon }}_{21}.\end{aligned}}}$

Строгое предположение экзогенности тогда подразумевает, что

${\displaystyle \operatorname {E} \left[({\overline {y}}_{11}-{\overline {y}}_{12})-({\overline {y}}_{21}-{\overline {y}}_{22})\right]~=~\delta (D_{11}-D_{12})+\delta (D_{22}-D_{21}).}$

Без потери общности предположим, что — группа лечения, а — последующий период, тогда и , что дает оценку DID ${\displaystyle s=2}$ ${\displaystyle t=2}$ ${\displaystyle D_{22}=1}$ ${\displaystyle D_{11}=D_{12}=D_{21}=0}$

${\displaystyle {\hat {\delta }}~=~({\overline {y}}_{11}-{\overline {y}}_{12})-({\overline {y}}_{21}-{\overline {y}}_{22}),}$

что можно интерпретировать как эффект лечения, обозначенный . Ниже показано, как эту оценку можно прочитать как коэффициент в обычной регрессии наименьших квадратов. Модель, описанная в этом разделе, чрезмерно параметризована; чтобы исправить это, один из коэффициентов для фиктивных переменных можно установить равным 0, например, мы можем установить . ${\displaystyle D_{st}}$ ${\displaystyle \gamma _{1}=0}$

Предположения

Иллюстрация предположения о параллельной тенденции

Все предположения модели OLS в равной степени применимы к DID. Кроме того, DID требует предположения о параллельной тенденции . Предположение о параллельной тенденции гласит, что одинаковы в обоих случаях и . Учитывая, что формальное определение выше точно отражает реальность, это предположение автоматически выполняется. Однако модель с вполне может быть более реалистичной. Чтобы повысить вероятность выполнения предположения о параллельной тенденции, подход «разница в разностях» часто сочетается с сопоставлением . ^[4] Это включает «сопоставление» известных единиц «лечения» с имитированными контрфактическими единицами «контроля»: характерно эквивалентными единицами, которые не получали лечения. Определяя переменную результата как временную разницу (изменение наблюдаемого результата между периодами до и после лечения) и сопоставление нескольких единиц в большой выборке на основе схожих историй до лечения, результирующий ATE (т. е. ATT: средний эффект лечения для пролеченных) обеспечивает надежную оценку разницы в разностях эффектов лечения. Это служит двум статистическим целям: во-первых, при условии наличия ковариатов до обработки предположение о параллельных тенденциях, скорее всего, будет верным; во-вторых, этот подход снижает зависимость от сопутствующих предположений об игнорируемости, необходимых для обоснованного вывода. ${\displaystyle \lambda _{2}-\lambda _{1}}$ ${\displaystyle s=1}$ ${\displaystyle s=2}$ ${\displaystyle \lambda _{st}~:~\lambda _{22}-\lambda _{21}\neq \lambda _{12}-\lambda _{11}}$

Как показано справа, эффект лечения — это разница между наблюдаемым значением y и тем, каким было бы значение y при параллельных тенденциях, если бы не было лечения. Ахиллесова пята DID — это когда что-то, кроме лечения, меняется в одной группе, но не в другой одновременно с лечением, что подразумевает нарушение предположения о параллельной тенденции.

Чтобы гарантировать точность оценки DID, предполагается, что состав индивидуумов двух групп остается неизменным с течением времени. При использовании модели DID необходимо учитывать и решать различные проблемы, которые могут скомпрометировать результаты, такие как автокорреляция ^[5] и провалы Эшенфельтера.

Выполнение

Метод DID может быть реализован в соответствии с таблицей ниже, где нижняя правая ячейка представляет собой оценку DID.

Проведение регрессионного анализа дает тот же результат. Рассмотрим модель OLS

${\displaystyle y~=~\beta _{0}+\beta _{1}T+\beta _{2}S+\beta _{3}(T\cdot S)+\varepsilon }$

где — фиктивная переменная для периода, равная , а — фиктивная переменная для членства в группе, равная . Составная переменная — фиктивная переменная, указывающая , когда . Хотя здесь это не показано строго, это правильная параметризация формального определения модели, более того, оказывается, что средние значения по группе и периоду в этом разделе связаны с оценками параметров модели следующим образом ${\displaystyle T}$ ${\displaystyle 1}$ ${\displaystyle t=2}$ ${\displaystyle S}$ ${\displaystyle 1}$ ${\displaystyle s=2}$ ${\displaystyle (T\cdot S)}$ ${\displaystyle S=T=1}$

${\displaystyle {\begin{aligned}{\hat {\beta }}_{0}&={\widehat {E}}(y\mid T=0,~S=0)\\[8pt]{\hat {\beta }}_{1}&={\widehat {E}}(y\mid T=1,~S=0)-{\widehat {E}}(y\mid T=0,~S=0)\\[8pt]{\hat {\beta }}_{2}&={\widehat {E}}(y\mid T=0,~S=1)-{\widehat {E}}(y\mid T=0,~S=0)\\[8pt]{\hat {\beta }}_{3}&={\big [}{\widehat {E}}(y\mid T=1,~S=1)-{\widehat {E}}(y\mid T=0,~S=1){\big ]}\\&\qquad {}-{\big [}{\widehat {E}}(y\mid T=1,~S=0)-{\widehat {E}}(y\mid T=0,~S=0){\big ]},\end{aligned}}}$

где обозначает условные средние значения, вычисленные по выборке, например, — показатель для последующего периода, — показатель для контрольной группы. Обратите внимание, что — оценка контрфактуального значения, а не влияние контрольной группы. Контрольная группа часто используется в качестве заменителя контрфактуального значения (см. Синтетический метод контроля для более глубокого понимания этого момента). Таким образом, можно интерпретировать как влияние как контрольной группы, так и контрфактуального значения вмешательства (лечения). Аналогично, , из-за предположения о параллельной тенденции, также является той же разницей между лечебной и контрольной группами в . Приведенные выше описания не следует толковать как подразумевающие (средний) эффект только контрольной группы для или только разницу лечебной и контрольной групп в предшествующий период для . Как и в случае Карда и Крюгера ниже, первая (временная) разность выходной переменной устраняет необходимость во временном тренде (т. е. ) для формирования несмещенной оценки , подразумевая, что это на самом деле не обусловлено группой лечения или контрольной группой. ^[6] Соответственно, разница между группами лечения и контрольной группой устранит необходимость в дифференциалах лечения (т. е. ) для формирования несмещенной оценки . Этот нюанс важно понимать, когда пользователь полагает, что существуют (слабые) нарушения параллельного пре-тренда или в случае нарушений соответствующих предположений контрфактуальной аппроксимации с учетом существования нетипичных шоков или искажающих событий. Чтобы увидеть связь между этой записью и предыдущим разделом, рассмотрим, как и выше, только одно наблюдение за период времени для каждой группы, тогда ${\displaystyle {\widehat {E}}(\dots \mid \dots )}$ ${\displaystyle T=1}$ ${\displaystyle S=0}$ ${\displaystyle {\hat {\beta }}_{1}}$ ${\displaystyle {\hat {\beta }}_{1}}$ ${\displaystyle {\hat {\beta }}_{2}}$ ${\displaystyle T=1}$ ${\displaystyle {\hat {\beta }}_{1}}$ ${\displaystyle {\hat {\beta }}_{2}}$ ${\displaystyle (\Delta Y_{i}=Y_{i,1}-Y_{i,0})}$ ${\displaystyle {\hat {\beta }}_{1}}$ ${\displaystyle {\hat {\beta }}_{3}}$ ${\displaystyle {\hat {\beta }}_{1}}$ ${\displaystyle {\hat {\beta }}_{2}}$ ${\displaystyle {\hat {\beta }}_{3}}$

${\displaystyle {\begin{aligned}{\widehat {E}}(y\mid T=1,~S=0)&={\widehat {E}}(y\mid {\text{ after period, control}})\\[3pt]\\&={\frac {{\widehat {E}}(y\ I({\text{ after period, control}}))}{{\widehat {P}}({\text{ after period, control}})}}\\[3pt]\\&={\frac {\sum _{i=1}^{n}y_{i,{\text{after}}}I(i{\text{ in control}})}{n_{\text{control}}}}={\overline {y}}_{\text{control, after}}\\[3pt]\\&={\overline {y}}_{\text{12}}\end{aligned}}}$

и так далее для других значений и , что эквивалентно ${\displaystyle T}$ ${\displaystyle S}$

${\displaystyle {\hat {\beta }}_{3}~=~(y_{11}-y_{21})-(y_{12}-y_{22}).}$

Но именно это выражение для эффекта лечения было дано в формальном определении и в приведенной выше таблице.

Пример

Статья Карда и Крюгера о минимальной заработной плате в Нью-Джерси , опубликованная в 1994 году, ^[6] считается одним из самых известных исследований DID; Кард позже был удостоен Нобелевской премии по экономике 2021 года отчасти за эту и связанную с ней работу. Кард и Крюгер сравнили занятость в секторе быстрого питания в Нью-Джерси и в Пенсильвании в феврале 1992 года и в ноябре 1992 года, после того как минимальная заработная плата в Нью-Джерси выросла с 4,25 до 5,05 долларов в апреле 1992 года. Наблюдение за изменением занятости только в Нью-Джерси, до и после лечения, не позволило бы контролировать пропущенные переменные, такие как погода и макроэкономические условия региона. Включая Пенсильванию в качестве контроля в модель «разница в разностях», любое смещение, вызванное переменными, общими для Нью-Джерси и Пенсильвании, неявно контролируется, даже если эти переменные не наблюдаются. Если предположить, что Нью-Джерси и Пенсильвания имеют параллельные тенденции с течением времени, то изменение занятости в Пенсильвании можно интерпретировать как изменение, которое испытал бы Нью-Джерси, если бы они не повысили минимальную заработную плату, и наоборот. Данные свидетельствуют о том, что повышение минимальной заработной платы не привело к снижению занятости в Нью-Джерси, вопреки тому, что предполагает некоторая экономическая теория. В таблице ниже показаны оценки Card & Krueger эффекта лечения на занятость, измеренного в FTE (или эквивалентах полной занятости) . Card и Krueger подсчитали, что повышение минимальной заработной платы на 0,80 доллара в Нью-Джерси привело к увеличению занятости на 2,75 FTE.

Пример программного обеспечения для этого исследования можно найти в команде Stata -diff- ^[7], автором которой является Хуан Мигель Вилья.

Смотрите также

• Планирование экспериментов
• Средний эффект лечения
• Метод синтетического контроля

Ссылки

1. Абади, А. (2005). «Полупараметрические оценки разности разностей». Обзор экономических исследований . 72 (1): 1–19. CiteSeerX  10.1.1.470.1475 . doi :10.1111/0034-6527.00321. S2CID  8801460.
2. Бертран, М.; Дюфло, Э .; Муллайнатан, С. (2004). «Насколько мы должны доверять оценкам разностей разностей?» (PDF) . Quarterly Journal of Economics . 119 (1): 249–275. doi :10.1162/003355304772839588. S2CID  470667.
3. Angrist, JD; Pischke, JS (2008). Mostly Harmless Econometrics: An Empiricist's Companion. Princeton University Press. С. 227–243. ISBN 978-0-691-12034-8.
4. Басу, Паллави; Смолл, Дилан (2020). «Построение более близкой контрольной группы в анализе различий в различиях: ее влияние на историю, взаимодействующую с групповым смещением». Observational Studies . 6 : 103–130. doi : 10.1353/obs.2020.0011. S2CID  221702893.
5. Бертран, Марианна; Дюфло, Эстер; Муллайнатан, Сендхил (2004). «Насколько мы должны доверять оценкам разниц в разностях?» (PDF) . Quarterly Journal of Economics . 119 (1): 249–275. doi :10.1162/003355304772839588. S2CID  470667.
6. Card, David; Krueger, Alan B. (1994). «Минимальная заработная плата и занятость: исследование индустрии быстрого питания в Нью-Джерси и Пенсильвании». American Economic Review . 84 (4): 772–793. JSTOR  2118030.
7. Вилла, Хуан М. (2016). "diff: упрощение оценки эффектов лечения «разница в разнице». The Stata Journal . 16 (1): 52–71. doi : 10.1177/1536867X1601600108 . S2CID  124464636.

Дальнейшее чтение

• Angrist, JD; Pischke, JS (2008). В основном безвредная эконометрика: спутник эмпирика. Princeton University Press. С. 227–243. ISBN 978-0-691-12034-8.
• Кэмерон, Артур К.; Триведи, Правин К. (2005). Микроэконометрика: методы и приложения . Издательство Кембриджского университета. С. 768–772. doi :10.1017/CBO9780511811241. ISBN 9780521848053. S2CID  120313863.
• Imbens, Guido W.; Wooldridge, Jeffrey M. (2009). «Последние разработки в эконометрике оценки программ». Журнал экономической литературы . 47 (1): 5–86. doi :10.1257/jel.47.1.5.
• Бакия, Джон; Хейм, Брэдли (август 2008 г.). «Как благотворительные пожертвования реагируют на стимулы и доход? Динамические панельные оценки с учетом предсказуемых изменений в налогообложении». Рабочий документ NBER № 14237. doi : 10.3386 /w14237 .
• Конли, Т.; Табер, К. (июль 2005 г.). «Вывод с „разницей в различиях“ при небольшом количестве изменений политики». Технический рабочий документ NBER № 312. doi : 10.3386 /t0312 .

Внешние ссылки

• Разница в оценке разницы, веб-сайт Healthcare Economist