Метод аналитических таблиц

Инструмент для доказательства логической формулы

Графическое представление частично построенной пропозициональной таблицы.

В теории доказательств семантическая таблица ^[1] ( / t æ ˈ b l oʊ , ˈ t æ b l oʊ / ; множественное число: таблицы ), также называемая аналитической таблицей , ^[2] деревом истинности , ^[1] или просто деревом , ^[2] представляет собой процедуру решения для сентенциальной и родственных логик, а также процедуру доказательства для формул логики первого порядка . ^[1] Аналитическая таблица — это древовидная структура, рассчитанная для логической формулы, имеющая в каждом узле подформулу исходной формулы, которую необходимо доказать или опровергнуть. Вычисления создают это дерево и используют его для доказательства или опровержения всей формулы. ^[3] Табличный метод позволяет также определить выполнимость конечных наборов формул различной логики. Это самая популярная процедура доказательства модальной логики . ^[4]

Метод деревьев истинности содержит фиксированный набор правил для создания деревьев из заданной логической формулы или набора логических формул. Эти деревья будут иметь больше формул на каждой ветви, и в некоторых случаях ветвь может содержать как формулу, так и ее отрицание, то есть противоречие. В этом случае говорят, что ветка закрывается . ^[1] Если каждая ветвь дерева закрывается, говорят, что само дерево закрывается. В силу правил построения таблиц замкнутое дерево является доказательством того, что исходная формула или набор формул, использованных для его построения, сама по себе противоречила ^[1] и, следовательно, была ложной. И наоборот, таблица также может доказать, что логическая формула тавтологична : если формула тавтологична, ее отрицание является противоречием, поэтому таблица, построенная на основе ее отрицания, закроется. ^[1]

История

В своей «Символической логике, часть II» Чарльз Лютвидж Доджсон (также известный под своим литературным псевдонимом Льюис Кэрролл) представил метод деревьев — самое раннее современное использование дерева истинности. ^[5]

Метод семантических таблиц был изобретен голландским логиком Эвертом Виллемом Бетом (Beth 1955) ^[6] и упрощен для классической логики Раймондом Смалльяном (Smullyan 1968, 1995). ^[7] Здесь описано упрощение Смалляна, «односторонние таблицы». Метод Смалляна был обобщен Уолтером Карниелли (Carnielli 1987) на произвольные многозначные пропозициональные логики и логики первого порядка . ^[8]

Таблицы можно интуитивно рассматривать как перевернутые последовательные системы . Эта симметричная связь между таблицами и секвенциальными системами была формально установлена ​​в (Carnielli 1991). ^[9]

Логика высказываний

Фон

Формула в логике высказываний состоит из букв, которые обозначают предложения, и связок, обозначающих конъюнкцию , дизъюнкцию , условные предложения , двуусловные предложения и отрицание . Истинность или ложность высказывания называется его истинностным значением. Формула или набор формул считается выполнимой, если существует возможность присвоения истинностных значений пропозициональным буквам так, что вся формула, сочетающая буквы со связками, сама по себе также истинна. ^[1] Говорят, что такое присвоение удовлетворяет формуле. ^[2]

Таблица проверяет, является ли данный набор формул выполнимым или нет. Ее можно использовать для проверки достоверности или следствия: формула действительна, если ее отрицание невыполнимо, а формулы подразумевают , если оно невыполнимо. ${\displaystyle A_{1},\ldots ,A_{n}}$ ${\displaystyle B}$ ${\displaystyle \{A_{1},\ldots ,A_{n},\neg B\}}$

В следующей таблице показаны некоторые варианты обозначений логических связок для читателей, которые, возможно, более знакомы с обозначениями, отличными от используемых здесь. В целом на момент включения этого предложения в тексте данной статьи использовался первый символ в каждой строке; однако, поскольку редакторы Википедии не обязаны использовать согласованные обозначения внутри или между статьями, это может измениться.

Общий метод

Основной принцип пропозициональных таблиц - попытаться «разбить» сложные формулы на более мелкие до тех пор, пока не будут созданы дополнительные пары литералов или дальнейшее расширение станет невозможным.

Исходная таблица для {(a⋁¬b)⋀b,¬a}

Метод работает с деревом, узлы которого помечены формулами. На каждом этапе это дерево модифицируется; в пропозициональном случае единственными разрешенными изменениями являются добавление узла как потомка листа. Процедура начинается с создания дерева, состоящего из цепочки всех формул набора для доказательства невыполнимости. ^[12] Тогда следующая процедура может быть применена неоднократно недетерминированно:

1. Выберите открытый листовой узел. (Листовой узел в исходной цепочке помечен как открытый).
2. Выберите подходящий узел на ветке над выбранным узлом. ^[13]
3. Примените соответствующий узел, который соответствует расширению дерева ниже выбранного конечного узла на основе некоторого правила расширения (подробно описано ниже).
4. Для каждого вновь созданного узла, который является одновременно литералом/отрицаемым литералом и дополнение которого появляется в предыдущем узле в той же ветви, пометьте ветвь как закрытую . Отметьте все остальные вновь созданные узлы как открытые .

В конце концов эта процедура завершится, потому что в какой-то момент будет применен каждый применимый узел, а правила расширения гарантируют, что каждый узел в дереве проще, чем применимый узел, использованный для его создания.

Принцип таблицы заключается в том, что формулы в узлах одной и той же ветви рассматриваются совместно, а различные ветви считаются разъединенными. В результате таблица представляет собой древовидное представление формулы, представляющей собой дизъюнкцию союзов. Эта формула эквивалентна набору для доказательства невыполнимости. Процедура модифицирует таблицу таким образом, что формула, представленная результирующей таблицей, эквивалентна исходной. Один из этих союзов может содержать пару дополнительных литералов, и в этом случае этот союз оказывается невыполнимым. Если окажется, что все конъюнкции невыполнимы, исходный набор формул невыполним.

И

(a⋁¬b)⋀b порождает a⋁¬b и b

Всякий раз, когда ветвь таблицы содержит формулу , представляющую собой соединение двух формул, обе эти формулы являются следствиями этой формулы. Этот факт можно формализовать следующим правилом расширения таблицы: ${\displaystyle A\wedge B}$

( ) Если ветвь таблицы содержит конъюнктивную формулу , добавим к ее листу цепочку из двух узлов, содержащих формулы и ${\displaystyle \wedge }$ ${\displaystyle A\wedge B}$ ${\displaystyle A}$ ${\displaystyle B}$

Обычно это правило записывается следующим образом:

${\displaystyle (\land ){\frac {A\wedge B}{\begin{array}{c}A\\B\end{array}}}}$

Вариант этого правила позволяет узлу содержать набор формул, а не одну. В этом случае формулы в этом наборе рассматриваются совместно, поэтому можно добавить в конец ветки, содержащей . Точнее, если узел на ветке помечен , к ветке можно добавить новый лист . ${\displaystyle \{A,B\}}$ ${\displaystyle A\wedge B}$ ${\displaystyle X\cup \{A\wedge B\}}$ ${\displaystyle X\cup \{A,B\}}$

Или

a⋁¬b генерирует a и ¬b

Если ветвь таблицы содержит формулу, являющуюся дизъюнкцией двух формул, например , можно применить следующее правило: ${\displaystyle A\vee B}$

( ) Если узел ветки содержит дизъюнктивную формулу , то создайте двух одноуровневых дочерних элементов листа ветки, содержащих формулы и , соответственно. ${\displaystyle \vee }$ ${\displaystyle A\vee B}$ ${\displaystyle A}$ ${\displaystyle B}$

Это правило разбивает ветвь на две части, отличающиеся только конечным узлом. Поскольку ветви рассматриваются в дизъюнкции друг к другу, то две результирующие ветви эквивалентны исходной, так как дизъюнкция их необщих узлов равна в точности . Правило дизъюнкции обычно формально записывается с использованием символа для разделения формул двух отдельных создаваемых узлов: ${\displaystyle A\vee B}$ ${\displaystyle |}$

${\displaystyle (\vee ){\frac {A\vee B}{A\mid B}}}$

Если предполагается, что узлы содержат наборы формул, это правило заменяется следующим: если узел помечен , к листу ветви, в которой находится этот узел, могут быть добавлены два родственных дочерних узла, помеченных и соответственно. ${\displaystyle Y\cup \{A\vee B\}}$ ${\displaystyle Y\cup \{A\}}$ ${\displaystyle Y\cup \{B\}}$

Нет

Целью таблиц является создание все более простых формул до тех пор, пока не будут созданы пары противоположных литералов или пока не станет возможным применить другое правило. Отрицание можно лечить, первоначально создавая формулы в нормальной форме отрицания , чтобы отрицание возникало только перед литералами. В качестве альтернативы можно использовать законы Де Моргана при расширении таблицы, так что, например, она рассматривается как . В этом случае также используются правила, которые вводят или удаляют пару отрицаний (например, в ) (в противном случае не было бы возможности расширить формулу, например : ${\displaystyle \neg (A\wedge B)}$ ${\displaystyle \neg A\vee \neg B}$ ${\displaystyle \neg \neg A}$ ${\displaystyle \neg \neg (A\wedge B))}$

${\displaystyle (\neg 1){\frac {A}{\neg \neg A}}}$

${\displaystyle (\neg 2){\frac {\neg \neg A}{A}}}$

Таблица закрыта

Закрытие

Каждую таблицу можно рассматривать как графическое представление формулы, эквивалентной набору, из которого построена таблица. Эта формула такова: каждая ветвь таблицы представляет собой конъюнкцию своих формул; таблица представляет собой дизъюнкция ее ветвей. Правила расширения преобразуют таблицу в таблицу, имеющую эквивалентную представленную формулу. Поскольку таблица инициализируется как одна ветвь, содержащая формулы входного набора, все последующие таблицы, полученные из нее, представляют собой формулы, эквивалентные этому набору (в варианте, где исходная таблица представляет собой единственный узел, помеченный как true, формулы, представленные таблицы являются следствием исходного набора.)

Таблица для выполнимого множества {a⋀c,¬a⋁b}: все правила были применены к каждой формуле в каждой ветви, но таблица не закрыта (закрыта только левая ветвь), как и ожидалось для выполнимых множеств.

Метод таблиц работает, начиная с исходного набора формул, а затем добавляя к таблице все более и более простые формулы, пока противоречие не будет показано в простой форме противоположных литералов. Поскольку формула, представленная таблицей, является дизъюнкцией формул, представленных ее ветвями, противоречие получается, когда каждая ветвь содержит пару противоположных литералов.

Если ветвь содержит литерал и его отрицание, соответствующая формула становится невыполнимой. В результате эту ветку теперь можно «закрыть», так как нет необходимости в дальнейшем ее расширении. Если все ветви таблицы закрыты, формула, представленная таблицей, невыполнима; следовательно, исходный набор также неудовлетворителен. Получение таблицы, в которой все ветви закрыты, является способом доказать невыполнимость исходного множества. В пропозициональном случае можно также доказать, что выполнимость доказывается невозможностью найти замкнутую таблицу при условии, что каждое правило разложения было применено везде, где оно могло быть применено. В частности, если таблица содержит несколько открытых (незакрытых) ветвей и каждая формула, не являющаяся литералом, использовалась правилом для создания нового узла в каждой ветви, в которой находится формула, набор является выполнимым.

Это правило учитывает, что формула может встречаться более чем в одной ветви (это тот случай, если есть хотя бы точка ветвления «ниже» узла). В этом случае необходимо применить правило расширения формулы, чтобы ее заключение(я) было добавлено ко всем этим ветвям, которые все еще открыты, прежде чем можно будет прийти к выводу, что таблица не может быть расширена дальше и что формула, следовательно, недействительна. удовлетворительно.

Таблица с метками множества

Вариант таблицы — пометить узлы наборами формул, а не отдельными формулами. В этом случае исходная таблица представляет собой один узел, помеченный набором, выполнимость которого необходимо доказать. Поэтому формулы в наборе считаются объединенными.

Правила расширения таблицы теперь могут работать с листьями таблицы, игнорируя все внутренние узлы. Для конъюнкции правило основано на эквивалентности множества, содержащего конъюнкцию, с множеством, содержащим оба, и вместо него. В частности, если лист помечен , к нему можно добавить узел с помощью метки : ${\displaystyle A\wedge B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle X\cup \{A\wedge B\}}$ ${\displaystyle X\cup \{A,B\}}$

${\displaystyle (\wedge ){\frac {X\cup \{A\wedge B\}}{X\cup \{A,B\}}}}$

Для дизъюнкции множество эквивалентно дизъюнкции двух множеств и . В результате, если первый набор помечает лист, к нему можно добавить двух дочерних элементов, помеченных двумя последними формулами. ${\displaystyle X\cup \{A\vee B\}}$ ${\displaystyle X\cup \{A\}}$ ${\displaystyle X\cup \{B\}}$

${\displaystyle (\vee ){\frac {X\cup \{A\vee B\}}{X\cup \{A\}|X\cup \{B\}}}}$

Наконец, если набор содержит как литерал, так и его отрицание, эту ветвь можно закрыть:

${\displaystyle (id){\frac {X\cup \{p,\neg p\}}{closed}}}$

Таблица для данного конечного множества X — это конечное (перевернутое) дерево с корнем X , в котором все дочерние узлы получены путем применения правил таблицы к их родителям. Ветка в такой таблице закрыта, если ее листовой узел содержит слово «закрыто». Таблица закрыта, если закрыты все ее ветви. Таблица открыта, если хотя бы одна ветвь не закрыта.

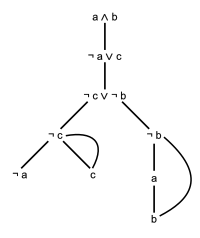
Ниже представлены две закрытые таблицы набора.

${\displaystyle X=\{r\wedge \neg r,\;p\wedge ((\neg p\vee q)\wedge \neg q)\}}$

Каждое применение правил отмечено справа. Оба достигают одинакового эффекта, первый закрывается быстрее. Единственная разница заключается в порядке выполнения сокращения.

${\displaystyle {\dfrac {\quad {\dfrac {\quad r\wedge \neg r,\;p\wedge ((\neg p\vee q)\wedge \neg q)\quad }{r,\;\neg r,\;p\wedge ((\neg p\vee q)\wedge \neg q)}}(\wedge )}{closed}}(\wedge )}$

и второй, более длинный, с правилами, применяемыми в другом порядке:

${\displaystyle {\dfrac {\quad {\dfrac {\quad {\dfrac {\quad r\wedge \neg r,\;p\wedge ((\neg p\vee q)\wedge \neg q)\quad }{r\wedge \neg r,\;p,\;((\neg p\vee q)\wedge \neg q)}}(\wedge )\quad }{r\wedge \neg r,\;p,\;(\neg p\vee q),\;\neg q}}(\wedge )}{\quad {\dfrac {\quad r\wedge \neg r,\;p,\;\neg p,\;\neg q\quad }{closed}}(id)\quad \quad {\dfrac {\quad r\wedge \neg r,\;p,\;q,\;\neg q\quad }{closed}}(id)}}(\vee )}$

Первая таблица закрывается только после одного применения правила, в то время как вторая не попадает в цель, и ее закрытие занимает гораздо больше времени. Очевидно, что мы предпочли бы всегда находить кратчайшие закрытые таблицы, но можно показать, что не может существовать единого алгоритма, который находит кратчайшие замкнутые таблицы для всех входных наборов формул.

Трех правил , приведенных выше, тогда достаточно, чтобы решить, является ли данный набор формул в отрицательной нормальной форме совместно выполнимым: ${\displaystyle (\wedge )}$ ${\displaystyle (\vee )}$ ${\displaystyle (id)}$ ${\displaystyle X'}$

Просто применяйте все возможные правила во всех возможных порядках, пока мы не найдем закрытую таблицу для или пока не исчерпаем все возможности и не придем к выводу, что каждая таблица для открыта. ${\displaystyle X'}$ ${\displaystyle X'}$

В первом случае совместно невыполнимо, а во втором случае листовой узел открытой ветви дает присвоение атомарным формулам и отрицательным атомарным формулам, что делает совместно выполнимым. Классическая логика на самом деле обладает довольно приятным свойством: нам нужно полностью исследовать только (любую) одну таблицу: если она замкнута, то она невыполнима, а если открыта, то выполнима. Но другие логики обычно не обладают этим свойством. ${\displaystyle X'}$ ${\displaystyle X'}$ ${\displaystyle X'}$ ${\displaystyle X'}$

Этих правил достаточно для всей классической логики, если взять исходный набор формул X и заменить каждый член C его логически эквивалентной отрицательной нормальной формой C', дающей набор формул X' . Мы знаем, что X выполнимо тогда и только тогда, когда X' выполнимо, поэтому достаточно найти замкнутую таблицу для X', используя процедуру, изложенную выше.

Постановкой мы можем проверить, является ли формула A тавтологией классической логики: ${\displaystyle X=\{\neg A\}}$

Если таблица закрытий невыполнима, то A является тавтологией, поскольку никакое присвоение значений истинности никогда не сделает A ложным. В противном случае любой открытый лист любой открытой ветви любой открытой таблицы for дает присваивание, которое фальсифицирует A . ${\displaystyle \{\neg A\}}$ ${\displaystyle \neg A}$ ${\displaystyle \{\neg A\}}$

Условный

Классическая логика высказываний обычно имеет связку для обозначения материальной импликации . Если мы напишем эту связку как ⇒, то формула A ⇒ B означает «если A , то B ». Можно дать табличное правило для разложения A ⇒ B на составляющие формулы. Аналогично мы можем дать по одному правилу для разделения каждого из ¬( A ∧ B ), ¬( A ∨ B ), ¬(¬ A ) и ¬( A ⇒ B ). Вместе эти правила дали бы завершающую процедуру для принятия решения о том, является ли данный набор формул одновременно выполнимым в классической логике, поскольку каждое правило разбивает одну формулу на ее составляющие, но ни одно правило не строит более крупные формулы из меньших составляющих. Таким образом, в конечном итоге мы должны достичь узла, содержащего только атомы и отрицания атомов. Если этот последний узел соответствует (id), мы можем закрыть ветку, в противном случае она остается открытой.

Но обратите внимание, что в классической логике выполняются следующие эквивалентности, где (...) = (...) означает, что формула левой части логически эквивалентна формуле правой части:

${\displaystyle {\begin{array}{lcl}\neg (A\land B)&=&\neg A\lor \neg B\\\neg (A\lor B)&=&\neg A\land \neg B\\\neg (\neg A)&=&A\\\neg (A\Rightarrow B)&=&A\land \neg B\\A\Rightarrow B&=&\neg A\lor B\\A\Leftrightarrow B&=&(A\land B)\lor (\neg A\land \neg B)\\\neg (A\Leftrightarrow B)&=&(A\land \neg B)\lor (\neg A\land B)\end{array}}}$

Если мы начнем с произвольной формулы C классической логики и неоднократно применим эти эквивалентности для замены левых частей правыми частями в C , то мы получим формулу C' , которая логически эквивалентна C , но которая обладает свойством что C' не содержит никаких значений, а ¬ появляется только перед атомарными формулами. Говорят, что такая формула находится в нормальной форме отрицания , и можно формально доказать, что каждая формула C классической логики имеет логически эквивалентную формулу C' в нормальной форме отрицания. То есть C выполнимо тогда и только тогда, когда C' выполнимо.

Пропозициональная таблица с объединением

Вышеупомянутые правила для пропозициональных таблиц можно упростить, используя единую систему обозначений. В единых обозначениях каждая формула относится либо к типу (альфа), либо к типу (бета). Каждой формуле типа альфа присваиваются два компонента , а каждой формуле типа бета — два компонента . Формулы типа альфа можно рассматривать как конъюнктивные, поскольку оба и подразумеваются как истинные. Формулы типа бета можно рассматривать как дизъюнктивные, поскольку либо или подразумевается как истина. В таблицах ниже показано, как определить тип и компоненты любой данной пропозициональной формулы: ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \alpha _{1},\alpha _{2}}$ ${\displaystyle \beta _{1},\beta _{2}}$ ${\displaystyle \alpha _{1}}$ ${\displaystyle \alpha _{2}}$ ${\displaystyle \alpha }$ ${\displaystyle \beta _{1}}$ ${\displaystyle \beta _{2}}$ ${\displaystyle \beta }$

${\displaystyle {\begin{array}{c|c|c}\alpha &\alpha _{1}&\alpha _{2}\\\hline X\wedge Y&X&Y\\\neg (X\vee Y)&\neg X&\neg Y\\\neg (X\implies Y)&X&\neg Y\\\neg \neg X&X&X\\\end{array}}}$ ${\displaystyle {\begin{array}{c|c|c}\beta &\beta _{1}&\beta _{2}\\\hline \neg (X\wedge Y)&\neg X&\neg Y\\X\vee Y&X&Y\\X\implies Y&\neg X&Y\\\neg \neg X&X&X\\\end{array}}}$

В каждой таблице в крайнем левом столбце показаны все возможные структуры формул типа альфа или бета, а в крайнем правом столбце показаны соответствующие компоненты. В качестве альтернативы правила единообразной записи можно выразить с помощью знаковых формул:

${\displaystyle {\begin{array}{c|c|c}\alpha &\alpha _{1}&\alpha _{2}\\\hline T\,X\wedge Y&T\,\,X&T\,\,Y\\F\,\,X\vee Y&F\,\,X&F\,\,Y\\F\,\,X\implies Y&T\,\,X&F\,\,Y\\F\,\,\neg X&T\,\,X&T\,\,Y\\T\,\,\neg X&F\,\,X&F\,\,Y\end{array}}\qquad {\begin{array}{c|c|c}\beta &\beta _{1}&\beta _{2}\\\hline F\,\,X\wedge Y&F\,\,Y&F\,\,X\\T\,\,X\vee Y&T\,\,X&T\,\,Y\\T\,\,X\implies Y&F\,\,X&T\,\,Y\\F\,\,\neg X&T\,\,X&T\,\,X\\T\,\,\neg X&F\,\,X&F\,\,Y\end{array}}}$

При построении пропозициональной таблицы с использованием приведенных выше обозначений всякий раз, когда встречается формула типа альфа, два ее компонента добавляются к текущей расширяемой ветви. Всякий раз, когда в какой-либо ветви встречается формула типа бета , ее можно разделить на две ветви: одну с набором { , } формул, а другую с набором { , } формул. ^[14] ${\displaystyle \alpha _{1},\alpha _{2}}$ ${\displaystyle \theta }$ ${\displaystyle \theta }$ ${\displaystyle \theta }$ ${\displaystyle \beta _{1}}$ ${\displaystyle \theta }$ ${\displaystyle \beta _{2}}$

Логическая таблица первого порядка

Таблицы расширяются до логики предикатов первого порядка с помощью двух правил для работы с универсальными и экзистенциальными кванторами соответственно. Можно использовать два разных набора правил; оба используют форму сколемизации для обработки кванторов существования, но различаются в обработке кванторов всеобщности.

Здесь предполагается, что набор формул для проверки достоверности не содержит свободных переменных; это не является ограничением, поскольку свободные переменные неявно выражаются количественно универсально, поэтому можно добавлять кванторы универсальности к этим переменным, в результате чего получается формула без свободных переменных.

Таблица первого порядка без объединения

Формула первого порядка подразумевает все формулы , где – основной член . Следовательно, следующее правило вывода является правильным: ${\displaystyle \forall x.\gamma (x)}$ ${\displaystyle \gamma (t)}$ ${\displaystyle t}$

${\displaystyle (\forall ){\frac {\forall x.\gamma (x)}{\gamma (t)}}}$где - произвольный основной член ${\displaystyle t}$

В отличие от правил для пропозициональных связок, может потребоваться многократное применение этого правила к одной и той же формуле. Например, набор может быть доказан только в том случае, если оба и порождены из . ${\displaystyle \{\neg P(a)\vee \neg P(b),\forall x.P(x)\}}$ ${\displaystyle P(a)}$ ${\displaystyle P(b)}$ ${\displaystyle \forall x.P(x)}$

Экзистенциальные кванторы рассматриваются посредством сколемизации. В частности, формула с ведущим квантором существования типа порождает свою сколемизацию , где – новый константный символ. ${\displaystyle \exists x.\delta (x)}$ ${\displaystyle \delta (c)}$ ${\displaystyle c}$

${\displaystyle (\exists ){\frac {\exists x.\delta (x)}{\delta (c)}}}$где новый постоянный символ ${\displaystyle c}$

Таблица без объединения для {∀xP(x), ∃x.(¬P(x)⋁¬P(f(x)))}. Для наглядности формулы пронумерованы слева, а формула и правило, используемые на каждом этапе, — справа.

Скулемский термин является константой (функцией арности 0), поскольку количественная оценка не входит в область действия какого-либо универсального квантора. Если исходная формула содержала какие-то кванторы всеобщности, так что квантификатор over находился в их пределах, то эти кванторы, очевидно, были удалены применением правила для кванторов всеобщности. ${\displaystyle c}$ ${\displaystyle x}$ ${\displaystyle x}$

Правило для кванторов существования вводит новые постоянные символы. Эти символы могут использоваться по правилу для кванторов всеобщности, так что они могут генерироваться, даже если не были в исходной формуле, но являются константой Скулема, созданной правилом для кванторов существования. ${\displaystyle \forall y.\gamma (y)}$ ${\displaystyle \gamma (c)}$ ${\displaystyle c}$

Два приведенных выше правила для кванторов всеобщности и существования верны, как и пропозициональные правила: если набор формул порождает замкнутую таблицу, этот набор невыполним. Полноту также можно доказать: если набор формул невыполним, то существует замкнутая таблица, построенная из него по этим правилам. Однако на самом деле обнаружение такой закрытой таблицы требует подходящей политики применения правил. В противном случае неудовлетворительный набор может породить бесконечно растущую таблицу. Например, набор неудовлетворителен, но закрытая таблица никогда не будет получена, если неразумно продолжать применять правило для кванторов универсальности к , генерируя, например , . Закрытую таблицу всегда можно найти, исключив эту и подобные «несправедливые» политики применения правил таблицы. ${\displaystyle \{\neg P(f(c)),\forall x.P(x)\}}$ ${\displaystyle \forall x.P(x)}$ ${\displaystyle P(c),P(f(c)),P(f(f(c))),\ldots }$

Правило для кванторов универсальности является единственным недетерминированным правилом, поскольку оно не определяет, какой термин создавать. Более того, хотя другие правила необходимо применять только один раз для каждой формулы и каждого пути, по которому находится формула, это правило может потребовать многократного применения. Однако применение этого правила можно ограничить, отложив его применение до тех пор, пока не перестанет применяться другое правило, а также ограничив применение правила основными терминами, которые уже появляются на пути таблицы. Показанный ниже вариант таблиц с унификацией направлен на решение проблемы недетерминизма. ${\displaystyle (\forall )}$

Таблица первого порядка с объединением

Основная проблема таблиц без унификации заключается в том, как выбрать основной термин для правила квантора универсальности. Действительно, можно использовать все возможные основные термины, но очевидно, что большинство из них могут быть бесполезны для завершения таблицы. ${\displaystyle t}$

Решением этой проблемы является «отсрочка» выбора термина до того момента, когда консеквент правила позволит закрыть хотя бы ветвь таблицы. Это можно сделать, используя переменную вместо термина, чтобы генерировать , а затем разрешить замены для последующей замены термином. Правило для кванторов универсальности выглядит следующим образом: ${\displaystyle \forall x.\gamma (x)}$ ${\displaystyle \gamma (x')}$ ${\displaystyle x'}$

${\displaystyle (\forall ){\frac {\forall x.\gamma (x)}{\gamma (x')}}}$где переменная не встречается нигде в таблице ${\displaystyle x'}$

Хотя предполагается, что исходный набор формул не содержит свободных переменных, формула таблицы может содержать свободные переменные, созданные по этому правилу. Эти свободные переменные неявно считаются универсально выраженными количественно.

В этом правиле вместо основного термина используется переменная. Этим изменением достигается то, что этим переменным можно будет затем присвоить значение, когда ветвь таблицы может быть закрыта, что решает проблему генерации термов, которые могут быть бесполезными.

Например, невыполнимость можно доказать, сначала сгенерировав ; отрицание этого литерала можно объединить с , наиболее общим унификатором является замена на ; применение этой замены приводит к замене на , которая закрывает таблицу. ${\displaystyle \{\neg P(a),\forall x.P(x)\}}$ ${\displaystyle P(x_{1})}$ ${\displaystyle \neg P(a)}$ ${\displaystyle x_{1}}$ ${\displaystyle a}$ ${\displaystyle P(x_{1})}$ ${\displaystyle P(a)}$

Это правило закрывает как минимум ветвь таблицы — ту, которая содержит рассматриваемую пару литералов. Однако замену необходимо применить ко всей таблице, а не только к этим двум литералам. Это выражается в том, что свободные переменные таблицы являются жесткими : если вхождение переменной заменяется чем-то другим, все остальные вхождения той же переменной должны быть заменены таким же образом. Формально свободные переменные (неявно) имеют универсальную количественную оценку, и все формулы таблицы находятся в пределах действия этих кванторов.

Экзистенциальные кванторы рассматриваются посредством сколемизации. В отличие от таблицы без унификации, скулемские термины не могут быть простыми константами. Действительно, формулы в таблице с унификацией могут содержать свободные переменные, которые неявно считаются универсально квантифицированными. В результате такая формула может входить в сферу действия кванторов всеобщности; если это так, то скулемский термин - это не простая константа, а термин, состоящий из нового функционального символа и свободных переменных формулы. ${\displaystyle \exists x.\delta (x)}$

${\displaystyle (\exists ){\frac {\exists x.\delta (x)}{\delta (f(x_{1},\ldots ,x_{n}))}}}$где — новый символ функции и свободные переменные ${\displaystyle f}$ ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle \delta }$

Таблица первого порядка с объединением для {∀xP(x), ∃x.(¬P(x)⋁¬P(f(x)))}. Для наглядности формулы пронумерованы слева, а формула и правило, используемые на каждом этапе, — справа.

Это правило включает в себя упрощение по сравнению с правилом, где являются свободными переменными ветви, а не одной. Это правило можно еще больше упростить за счет повторного использования символа функции, если он уже использовался в формуле, идентичной с точностью до переименования переменной. ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle \delta }$ ${\displaystyle \delta }$

Формула, представленная таблицей, получается способом, аналогичным пропозициональному случаю, с дополнительным предположением, что свободные переменные считаются универсально квантифицированными. Что касается пропозиционального случая, то формулы в каждой ветви соединяются, а полученные формулы разъединяются. Кроме того, все свободные переменные полученной формулы имеют универсальную количественную оценку. Все эти кванторы включают в себя всю формулу. Другими словами, если – формула, полученная расчленением конъюнкции формул каждой ветви, и – свободные переменные в ней, то – формула, представленная таблицей. Применимы следующие соображения: ${\displaystyle F}$ ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle \forall x_{1},\ldots ,x_{n}.F}$

• Предположение о том, что свободные переменные имеют универсальную количественную оценку, делает применение наиболее общего унификатора здравым правилом: поскольку означает, что это верно для любого возможного значения , то это верно и для термина , которым заменяет наиболее общий унификатор . ${\displaystyle \gamma (x')}$ ${\displaystyle \gamma }$ ${\displaystyle x'}$ ${\displaystyle \gamma (t)}$ ${\displaystyle t}$ ${\displaystyle x}$
• Свободные переменные в таблице являются жесткими: все вхождения одной и той же переменной должны быть заменены одним и тем же термином. Каждую переменную можно рассматривать как символ, обозначающий термин, решение по которому еще предстоит определить. Это следствие того, что свободные переменные считаются универсально квантифицированными по всей формуле, представленной таблицей: если одна и та же переменная встречается бесплатно в двух разных узлах, оба вхождения находятся в области действия одного и того же квантора. Например, если формулы в двух узлах — это и , где в обоих свободно, формула, представленная таблицей, имеет вид . Эта формула подразумевает, что это верно для любого значения , но, как правило, не подразумевает двух разных членов и , поскольку эти два термина обычно могут принимать разные значения. Это означает, что его нельзя заменить двумя разными терминами в и . ${\displaystyle A(x)}$ ${\displaystyle B(x)}$ ${\displaystyle x}$ ${\displaystyle \forall x.(...A(x)...B(x)...)}$ ${\displaystyle (...A(x)...B(x)...)}$ ${\displaystyle x}$ ${\displaystyle (...A(t)...A(t')...)}$ ${\displaystyle t}$ ${\displaystyle t'}$ ${\displaystyle x}$ ${\displaystyle A(x)}$ ${\displaystyle B(x)}$
• Свободные переменные в формуле для проверки достоверности также считаются универсально выраженными. Однако эти переменные нельзя оставлять свободными при построении таблицы, поскольку правила таблиц работают по принципу, обратному формуле, но по-прежнему рассматривают свободные переменные как универсально количественно определяемые. Например, неверно (неверно в модели где и интерпретации где ). Следовательно, выполнимо (оно удовлетворяется той же моделью и интерпретацией). Однако закрытую таблицу можно создать с помощью и , а замена на приведет к замыканию. Правильная процедура — сначала сделать явными кванторы универсальности, генерируя таким образом . ${\displaystyle P(x)\rightarrow P(c)}$ ${\displaystyle D=\{1,2\},P(1)=\bot ,P(2)=\top ,c=1}$ ${\displaystyle x=2}$ ${\displaystyle \{P(x),\neg P(c)\}}$ ${\displaystyle P(x)}$ ${\displaystyle \neg P(c)}$ ${\displaystyle x}$ ${\displaystyle c}$ ${\displaystyle \forall x.(P(x)\rightarrow P(c))}$

Следующие два варианта также верны.

• Применение замены свободных переменных таблицы ко всей таблице является правильным правилом при условии, что эта замена свободна для формулы, представляющей таблицу. В других мирах применение такой замены приводит к таблице, формула которой по-прежнему является следствием входного набора. Использование большинства общих унификаторов автоматически гарантирует выполнение условия свободы таблицы.
• Хотя обычно каждую переменную во всей таблице необходимо заменять одним и тем же термином, в некоторых особых случаях в этом нет необходимости.

Таблицы с объединением можно доказать полными: если набор формул невыполним, у него есть доказательство в виде таблицы с объединением. Однако на самом деле найти такое доказательство может оказаться трудной проблемой. В отличие от случая без унификации, применение замены может изменить существующую часть таблицы; хотя применение замены закрывает хотя бы одну ветвь, это может сделать невозможным закрытие других ветвей (даже если набор невыполним).

Решением этой проблемы является отложенное создание экземпляров : замена не применяется до тех пор, пока не будет найдена та, которая закроет все ветки одновременно. В этом варианте доказательство неудовлетворительного множества всегда можно найти с помощью подходящей политики применения других правил. Однако этот метод требует хранения всей таблицы в памяти: общий метод закрывает ветки, которые затем можно отбросить, а этот вариант не закрывает ни одну ветку до конца.

Проблема, заключающаяся в том, что некоторые таблицы, которые можно сгенерировать, невозможно закрыть, даже если множество невыполнимо, является общей для других наборов правил расширения таблиц: даже если некоторые конкретные последовательности применения этих правил позволяют построить замкнутую таблицу (если множество невыполнимо ), некоторые другие последовательности приводят к таблицам, которые невозможно закрыть. Общие решения для этих случаев изложены в разделе «Поиск таблицы».

Табличные исчисления и их свойства

Табличное исчисление — это набор правил, позволяющий строить и изменять таблицы. Пропозициональные правила таблиц, правила таблиц без унификации и правила таблиц с унификацией — все это табличные исчисления. Некоторые важные свойства, которыми табличное исчисление может обладать или не обладать, — это полнота, деструктивность и слияние доказательств.

Табличное исчисление называется полным, если оно позволяет построить табличное доказательство для каждого заданного невыполнимого набора формул. Упомянутое выше табличное исчисление можно доказать полным.

Замечательная разница между таблицей с объединением и двумя другими исчислениями состоит в том, что последние два исчисления изменяют таблицу только путем добавления к ней новых узлов, тогда как первое позволяет заменами изменять существующую часть таблицы. В более общем смысле табличные исчисления классифицируются как деструктивные или неразрушающие в зависимости от того, добавляют ли они только новые узлы в таблицу или нет. Таким образом, таблица с унификацией деструктивна, тогда как пропозициональная таблица и таблица без унификации недеструктивны.

Слияние доказательств - это свойство табличного исчисления, позволяющее получить доказательство для произвольного невыполнимого множества из произвольной таблицы, предполагая, что эта таблица сама была получена путем применения правил исчисления. Другими словами, в табличном исчислении с конфлюэнтными доказательствами к невыполнимому множеству можно применить любой набор правил и при этом получить таблицу, из которой можно получить замкнутую таблицу, применив некоторые другие правила.

Процедуры доказательства

Табличное исчисление — это просто набор правил, которые предписывают, как можно изменить таблицу. Процедура доказательства — это метод фактического поиска доказательства (если оно существует). Другими словами, табличное исчисление — это набор правил, а процедура доказательства — это политика применения этих правил. Даже если исчисление является полным, не каждый возможный выбор применения правил приводит к доказательству невыполнимого множества. Например, является невыполнимой, но как таблицы с объединением, так и таблицы без объединения допускают повторное применение правила кванторов всеобщности к последней формуле, тогда как простое применение правила дизъюнкции к третьей непосредственно привело бы к замыканию. ${\displaystyle \{P(f(c)),R(c),\neg P(f(c))\vee \neg R(c),\forall x.Q(x)\}}$

Для процедур доказательства дано определение полноты: процедура доказательства является сильно полной, если она позволяет найти замкнутую таблицу для любого заданного невыполнимого набора формул. Слияние доказательств основного исчисления имеет отношение к полноте: слияние доказательств - это гарантия того, что замкнутая таблица всегда может быть сгенерирована из произвольной частично построенной таблицы (если множество невыполнимо). Без слияния доказательств применение «неправильного» правила может привести к невозможности сделать таблицу полной за счет применения других правил.

Пропозициональные таблицы и таблицы без унификации имеют строго полные процедуры доказательства. В частности, полная процедура доказательства – это справедливое применение правил . Это связано с тем, что единственный способ, которым такие исчисления не могут создать замкнутую таблицу из невыполнимого множества, — это не применять некоторые применимые правила.

Для пропозициональных таблиц справедливость означает расширение каждой формулы в каждой ветви. Точнее, для каждой формулы и каждой ветви, в которой находится формула, правило, в котором формула является предварительным условием, используется для расширения ветви. Процедура справедливого доказательства для пропозициональных таблиц является строго полной.

Для таблиц первого порядка без унификации условие справедливости аналогичное, за исключением того, что правило для кванторов универсальности может потребовать более одного применения. Справедливость означает бесконечное расширение каждого квантора универсальности. Другими словами, справедливая политика применения правил не может продолжать применять другие правила без расширения каждого квантора универсальности в каждой ветви, которая все еще открыта время от времени.

Поиск закрытой таблицы

Если табличное исчисление является полным, каждому невыполнимому набору формул соответствует соответствующая закрытая таблица. Хотя эту таблицу всегда можно получить, применив некоторые правила исчисления, проблема того, какие правила применить к данной формуле, все еще остается. В результате полнота не означает автоматически существование осуществимой политики применения правил, которая всегда приводит к закрытой таблице для каждого данного невыполнимого набора формул. Хотя процедура справедливого доказательства является полной для основной таблицы и таблицы без объединения, это не относится к таблице с объединением.

Дерево поиска в пространстве таблиц для {∀xP(x), ¬P(c)⋁¬Q(c), ∃yQ(c)}. Для простоты формулы набора опущены во всех таблицах на рисунке, а вместо них использован прямоугольник. Закрытая таблица выделена жирным шрифтом; другие отрасли могут быть еще расширены.

Общим решением этой проблемы является поиск в пространстве таблиц до тех пор, пока не будет найдена замкнутая таблица (если она существует, то есть множество невыполнимо). В этом подходе мы начинаем с пустой таблицы, а затем рекурсивно применяем все возможные применимые правила. Эта процедура посещает (неявное) дерево, узлы которого помечены таблицами, и таблица в узле получается из таблицы в его родительском элементе путем применения одного из допустимых правил.

Поскольку каждая ветвь может быть бесконечной, это дерево необходимо посещать в ширину, а не в глубину. Для этого требуется большое пространство, так как ширина дерева может расти в геометрической прогрессии. Метод, который может посещать некоторые узлы более одного раза, но работает в полиномиальном пространстве, заключается в посещении в глубину с итеративным углублением : сначала посещается глубина дерева до определенной глубины, затем увеличивается глубина и выполняется посещение снова. . Эта конкретная процедура использует глубину (которая также представляет собой количество примененных правил таблицы) для принятия решения о том, когда остановиться на каждом шаге. Вместо этого использовались различные другие параметры (например, размер таблицы, маркирующей узел).

Сокращение поиска

Размер дерева поиска зависит от количества (дочерних) таблиц, которые можно сгенерировать из заданной (родительской) таблицы. Таким образом, уменьшение количества таких таблиц уменьшает требуемый поиск.

Способ уменьшить это число — запретить создание некоторых таблиц на основе их внутренней структуры. Примером может служить условие регулярности: если ветвь содержит литерал, использование правила расширения, генерирующего тот же литерал, бесполезно, поскольку ветвь, содержащая две копии литералов, будет иметь тот же набор формул, что и исходная. Это расширение можно запретить, поскольку если закрытая таблица существует, ее можно найти и без нее. Это ограничение является структурным, поскольку его можно проверить, просмотрев структуру таблицы только для ее расширения.

Различные методы сокращения поиска не позволяют создавать некоторые таблицы на том основании, что закрытую таблицу все же можно найти, расширив другие. Эти ограничения называются глобальными. В качестве примера глобального ограничения можно использовать правило, определяющее, какая из открытых ветвей должна быть расширена. В результате, если таблица имеет, например, две незакрытые ветви, правило определяет, какая из них должна быть расширена, запрещая расширение второй. Это ограничение уменьшает пространство поиска, поскольку теперь запрещен один возможный выбор; однако полнота не пострадает, поскольку вторая ветвь все равно будет расширена, если первая в конечном итоге закроется. Например, таблица с корнем , дочерним элементом и двумя листьями , которую можно закрыть двумя способами: применить сначала к , а затем к или наоборот. Очевидно, нет необходимости использовать обе возможности; можно рассматривать только случай, в котором оно применяется впервые, и игнорировать случай, в котором оно впервые применяется к . Это глобальное ограничение, поскольку пренебречь вторым расширением позволяет наличие другой таблицы, к которой расширение применяется сначала и потом. ${\displaystyle \neg a\wedge \neg b}$ ${\displaystyle a\vee b}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle (\wedge )}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle (\wedge )}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle b}$

Таблицы предложений

При применении к наборам предложений (а не к произвольным формулам) табличные методы позволяют повысить эффективность. Предложение первого порядка — это формула , которая не содержит свободных переменных и каждая из которых является литералом. Кванторы универсальности часто опускаются для ясности, так что, например, на самом деле это означает . Обратите внимание, что, если понимать эти две формулы буквально, это не то же самое, что и для выполнимости: скорее, выполнимость такая же, как у . То, что свободные переменные имеют универсальную количественную оценку, не является следствием определения выполнимости первого порядка; оно скорее используется как неявное общее предположение при работе с предложениями. ${\displaystyle \forall x_{1},\ldots ,x_{n}L_{1}\vee \cdots \vee L_{m}}$ ${\displaystyle L_{i}}$ ${\displaystyle P(x,y)\vee Q(f(x))}$ ${\displaystyle \forall x,y.P(x,y)\vee Q(f(x))}$ ${\displaystyle P(x,y)\vee Q(f(x))}$ ${\displaystyle \exists x,y.P(x,y)\vee Q(f(x))}$

Единственные правила расширения, применимые к предложению, — это и ; эти два правила можно заменить их комбинацией без потери полноты. В частности, следующее правило соответствует последовательному применению правил исчисления первого порядка с унификацией. ${\displaystyle (\forall )}$ ${\displaystyle (\vee )}$ ${\displaystyle (\forall )}$ ${\displaystyle (\vee )}$

${\displaystyle (C){\frac {L_{1}\vee \cdots \vee L_{n}}{L_{1}'|\cdots |L_{n}'}}}$где получается заменой каждой переменной новой в ${\displaystyle L_{1}'\vee \cdots \vee L_{n}'}$ ${\displaystyle L_{1}\vee \cdots \vee L_{n}}$

Когда набор, подлежащий проверке на выполнимость, состоит только из предложений, этого и правил унификации достаточно для доказательства невыполнимости. В других мирах таблица исчислений состоит из и является полной. ${\displaystyle (C)}$ ${\displaystyle (\sigma )}$

Поскольку правило расширения предложений генерирует только литералы и никогда не генерирует новые предложения, предложения, к которым оно может быть применено, являются только предложениями входного набора. В результате правило расширения предложения может быть дополнительно ограничено случаем, когда предложение находится во входном наборе.

${\displaystyle (C){\frac {L_{1}\vee \cdots \vee L_{n}}{L_{1}'|\cdots |L_{n}'}}}$где получается заменой каждой переменной новой в , которая является частью входного набора ${\displaystyle L_{1}'\vee \cdots \vee L_{n}'}$ ${\displaystyle L_{1}\vee \cdots \vee L_{n}}$

Поскольку это правило напрямую использует предложения входного набора, нет необходимости инициализировать таблицу цепочкой входных предложений. Таким образом, исходную таблицу можно инициализировать с помощью единственного узла с меткой ; этот ярлык часто опускается как неявный. В результате этого дальнейшего упрощения каждый узел таблицы (кроме корня) помечен литералом. ${\displaystyle true}$

Для таблицы предложений можно использовать ряд оптимизаций. Эта оптимизация направлена ​​на уменьшение количества возможных таблиц, которые необходимо исследовать при поиске закрытой таблицы, как описано в разделе «Поиск закрытой таблицы» выше.

Таблица соединений

Соединение — это условие таблицы, которое запрещает расширение ветки с помощью предложений, не связанных с литералами, которые уже находятся в ветке. Соединение можно определить двумя способами:

сильная связанность

при расширении ветки используйте входное предложение только в том случае, если оно содержит литерал, который можно унифицировать с отрицанием литерала в текущем листе

слабая связность

allow the use of clauses that contain a literal that unifies with the negation of a literal on the branch

Both conditions apply only to branches consisting not only of the root. The second definition allows for the use of a clause containing a literal that unifies with the negation of a literal in the branch, while the first only further constraint that literal to be in leaf of the current branch.

If clause expansion is restricted by connectedness (either strong or weak), its application produces a tableau in which substitution can applied to one of the new leaves, closing its branch. In particular, this is the leaf containing the literal of the clause that unifies with the negation of a literal in the branch (or the negation of the literal in the parent, in case of strong connection).

Both conditions of connectedness lead to a complete first-order calculus: if a set of clauses is unsatisfiable, it has a closed connected (strongly or weakly) tableau. Such a closed tableau can be found by searching in the space of tableaux as explained in the "Searching for a closed tableau" section. During this search, connectedness eliminates some possible choices of expansion, thus reducing search. In other worlds, while the tableau in a node of the tree can be in general expanded in several different ways, connection may allow only few of them, thus reducing the number of resulting tableaux that need to be further expanded.

This can be seen on the following (propositional) example. The tableau made of a chain ${\displaystyle true-a}$ for the set of clauses ${\displaystyle \{a,\neg a\vee b,\neg c\vee d,\neg b\}}$ can be in general expanded using each of the four input clauses, but connection only allows the expansion that uses ${\displaystyle \neg a\vee b}$. This means that the tree of tableaux has four leaves in general but only one if connectedness is imposed. This means that connectedness leaves only one tableau to try to expand, instead of the four ones to consider in general. In spite of this reduction of choices, the completeness theorem implies that a closed tableau can be found if the set is unsatisfiable.

Условия связности, примененные к пропозициональному (клаузальному) падежу, делают результирующее исчисление несливным. Как пример, невыполнимо, но применение к порождает цепочку , которая не является замкнутой и к которой нельзя применить никакое другое правило разложения без нарушения ни сильной, ни слабой связности. В случае слабой связности слияние имеет место при условии, что предложение, используемое для расширения корня, релевантно невыполнимости, то есть содержится в минимально невыполнимом подмножестве множества предложений. К сожалению, проблема проверки того, соответствует ли предложение этому условию, сама по себе является сложной проблемой. Несмотря на несовпадение, закрытую таблицу можно найти с помощью поиска, как показано в разделе «Поиск закрытой таблицы» выше. Хотя поиск необходим, связность уменьшает возможные варианты расширения, что делает поиск более эффективным. ${\displaystyle \{a,b,\neg b\}}$ ${\displaystyle (C)}$ ${\displaystyle a}$ ${\displaystyle true-a}$

Регулярные таблицы

Таблица является регулярной, если ни один литерал не встречается дважды в одной и той же ветви. Обеспечение соблюдения этого условия позволяет сократить количество возможных вариантов расширения таблицы, поскольку предложения, которые могут создать нерегулярную таблицу, не могут быть расширены.

Однако эти запрещенные шаги расширения бесполезны. Если — ветвь, содержащая литерал , и предложение, раскрытие которого нарушает регулярность, то содержит . Чтобы закрыть таблицу, необходимо, среди прочего, развернуть и закрыть ветку, где , где встречается дважды. Однако формулы в этой ветке точно такие же, как и формулы в одиночестве. В результате те же шаги расширения, которые закрываются, также закрываются . Это означает, что расширение было ненужным; более того, если он содержал другие литералы, его раскрытие порождало другие листы, которые нужно было закрыть. В пропозициональном случае расширение, необходимое для закрытия этих листьев, совершенно бесполезно; в случае первого порядка они могут повлиять на остальную часть таблицы только из-за некоторых унификаций; однако их можно объединить с заменами, используемыми для закрытия остальной части таблицы. ${\displaystyle B}$ ${\displaystyle L}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle L}$ ${\displaystyle B-L}$ ${\displaystyle L}$ ${\displaystyle B}$ ${\displaystyle B-L}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle C}$

Таблицы для модальной логики

В модальной логике модель включает в себя набор возможных миров , каждый из которых связан с оценкой истинности; отношение доступности определяет, когда один мир доступен из другого. Модальная формула может задавать не только условия над возможным миром, но и над теми, которые доступны из него. Например, верно в мире, если верно во всех мирах, доступных из него. ${\displaystyle \Box A}$ ${\displaystyle A}$

Что касается логики высказываний, то таблицы модальной логики основаны на рекурсивном разбиении формул на их основные компоненты. Однако расширение модальной формулы может потребовать указания условий в разных мирах. Например, если в мире истинно, то существует мир, доступный из него, где оно ложно. Однако нельзя просто добавить к пропозициональным следующее правило. ${\displaystyle \neg \Box A}$ ${\displaystyle A}$

${\displaystyle {\frac {\neg \Box A}{\neg A}}}$

В пропозициональных таблицах все формулы относятся к одной и той же оценке истинности, но предварительное условие приведенного выше правила справедливо в одном мире, а следствие — в другом. Если не принять это во внимание, результаты будут неверными. Например, формула утверждает, что это истинно в текущем мире и ложно в мире, доступном из нее. Простое применение приведенного выше правила разложения приведет к получению и , но эти две формулы в целом не должны вызывать противоречия, поскольку они справедливы в разных мирах. Модальные табличные исчисления содержат правила, подобные приведенным выше, но включают в себя механизмы, позволяющие избежать неправильного взаимодействия формул, относящихся к разным мирам. ${\displaystyle a\wedge \neg \Box a}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle (\wedge )}$ ${\displaystyle a}$ ${\displaystyle \neg a}$

Технически таблицы модальной логики проверяют выполнимость набора формул: они проверяют, существует ли модель и мир , в которых формулы в наборе истинны в этой модели и мире. В приведенном выше примере, хотя формула утверждает истинность in , формула устанавливает истинность некоторого мира , который доступен из и который в целом может отличаться от . Табличные исчисления для модальной логики учитывают, что формулы могут относиться к разным мирам. ${\displaystyle M}$ ${\displaystyle w}$ ${\displaystyle a}$ ${\displaystyle a}$ ${\displaystyle w}$ ${\displaystyle \neg \Box a}$ ${\displaystyle \neg a}$ ${\displaystyle w'}$ ${\displaystyle w}$ ${\displaystyle w}$

Этот факт имеет важное следствие: формулы, действующие в мире, могут подразумевать условия для различных преемников этого мира. Невыполнимость затем можно доказать с помощью подмножества формул, относящихся к одному преемнику. Это справедливо, если мир может иметь более одного преемника, что верно для большинства модальных логик. В этом случае формула типа true будет верна, если существует преемник, в котором выполняется удержание, и преемник, в котором существует удержание. И наоборот, если можно показать невыполнимость для произвольного преемника, формула оказывается невыполнимой без проверки миров, в которых она выполняется. В то же время, если можно показать невыполнимость , нет необходимости проверять . В результате, хотя существует два возможных способа разложения , одного из этих двух способов всегда достаточно, чтобы доказать невыполнимость, если формула невыполнима. Например, можно расширить таблицу, рассмотрев произвольный мир, в котором выполняется. Если это расширение приводит к невыполнимости, исходная формула невыполнима. Однако также возможно, что невыполнимость не может быть доказана таким способом и вместо этого следует рассматривать мир, в котором выполняется. В результате всегда можно доказать невыполнимость, расширяя либо только, либо только; однако, если сделан неправильный выбор, результирующую таблицу нельзя закрыть. Расширение любой подформулы приводит к табличным исчислениям, которые являются полными, но не слитными по доказательству. Поэтому может потребоваться поиск, как описано в разделе «Поиск закрытой таблицы». ${\displaystyle \neg \Box A\wedge \neg \Box B}$ ${\displaystyle \neg A}$ ${\displaystyle \neg B}$ ${\displaystyle \neg A}$ ${\displaystyle \neg B}$ ${\displaystyle \neg B}$ ${\displaystyle \neg A}$ ${\displaystyle \neg \Box A\wedge \neg \Box B}$ ${\displaystyle \neg A}$ ${\displaystyle \neg B}$ ${\displaystyle \neg \Box A}$ ${\displaystyle \neg \Box B}$

В зависимости от того, относятся ли предварительное условие и следствие правила расширения таблицы к одному и тому же миру или нет, правило называется статическим или транзакционным. Хотя все правила для пропозициональных связок статичны, не все правила для модальных связок являются транзакционными: например, в каждой модальной логике, включая аксиому T , выполняется утверждение, что подразумевается в одном и том же мире. В результате правило относительного (модального) расширения таблицы является статическим, поскольку и его предусловие, и следствие относятся к одному и тому же миру. ${\displaystyle \Box A}$ ${\displaystyle A}$

Таблица удаления формул

Способ избежать неправильного взаимодействия формул, относящихся к разным мирам, состоит в том, чтобы убедиться, что все формулы ветки относятся к одному и тому же миру. Изначально это условие верно, поскольку предполагается, что все формулы в наборе, проверяемом на непротиворечивость, относятся к одному и тому же миру. При расширении ветки возможны две ситуации: либо новые формулы относятся к тому же миру, что и другая в ветке, либо нет. В первом случае правило применяется нормально. Во втором случае все формулы ветви, которые не выполняются также в новом мире, удаляются из ветви и, возможно, добавляются ко всем другим ветвям, которые все еще относятся к старому миру.

Например, в S5 каждая формула , которая верна в мире, также верна и во всех доступных мирах (то есть во всех доступных мирах истинны оба и ). Следовательно, при применении , последствия которого справедливы в другом мире, можно удалить все формулы из ветви, но можно сохранить все формулы , поскольку они справедливы и в новом мире. Чтобы сохранить полноту, удаленные формулы затем добавляются ко всем другим ветвям, которые все еще относятся к старому миру. ${\displaystyle \Box A}$ ${\displaystyle A}$ ${\displaystyle \Box A}$ ${\displaystyle {\frac {\neg \Box B}{\neg B}}}$ ${\displaystyle \Box A}$

Всемирно известная картина

Другой механизм обеспечения правильного взаимодействия между формулами, относящимися к разным мирам, заключается в переключении от формул к помеченным формулам: вместо написания можно было бы написать, чтобы явно указать, что справедливо в world . ${\displaystyle A}$ ${\displaystyle w:A}$ ${\displaystyle A}$ ${\displaystyle w}$

Все правила пропозиционального расширения адаптируются к этому варианту, утверждая, что все они относятся к формулам с одним и тем же мировым ярлыком. Например, генерирует два узла, помеченные значками и ; ветка закрывается только в том случае, если она содержит два противоположных литерала одного мира, например и ; замыкание не генерируется, если две мировые метки различны, например, в и . ${\displaystyle w:A\wedge B}$ ${\displaystyle w:A}$ ${\displaystyle w:B}$ ${\displaystyle w:a}$ ${\displaystyle w:\neg a}$ ${\displaystyle w:a}$ ${\displaystyle w':\neg a}$

Правило модального расширения может иметь последствия, относящиеся к различным мирам. Например, правило для будет записано следующим образом ${\displaystyle \neg \Box A}$

${\displaystyle {\frac {w:\neg \Box A}{w':\neg A}}}$

Предусловие и следствие этого правила относятся к мирам и соответственно. Различные исчисления используют разные методы для отслеживания доступности миров, используемых в качестве меток. Некоторые включают псевдоформулы, обозначающие, что они доступны из . Некоторые другие используют последовательности целых чисел в качестве мировых меток, причем это обозначение неявно представляет отношение доступности (например, доступно из .) ${\displaystyle w}$ ${\displaystyle w'}$ ${\displaystyle wRw'}$ ${\displaystyle w'}$ ${\displaystyle w}$ ${\displaystyle (1,4,2,3)}$ ${\displaystyle (1,4,2)}$

Таблицы маркировки множеств

Проблему взаимодействия между формулами, содержащимися в разных мирах, можно решить, используя таблицы маркировки множеств. Это деревья, узлы которых помечены наборами формул; правила расширения объясняют, как присоединять к листу новые узлы, основываясь только на метке листа (а не на метках других узлов ветки).

Таблицы модальных логик используются для проверки выполнимости набора модальных формул в данной модальной логике. По набору формул они проверяют существование модели и мира такого, что . ${\displaystyle S}$ ${\displaystyle M}$ ${\displaystyle w}$ ${\displaystyle M,w\models S}$

Правила расширения зависят от конкретной используемой модальной логики. Систему таблиц для базовой модальной логики K можно получить, добавив к правилам пропозициональных таблиц следующее:

${\displaystyle (K){\frac {\Box A_{1};\ldots ;\Box A_{n};\neg \Box B}{A_{1};\ldots ;A_{n};\neg B}}}$

Интуитивно предусловие этого правила выражает истинность всех формул во всех доступных мирах и истинность некоторых доступных миров. Следствием этого правила является формула, которая должна быть верной в одном из тех миров, где она истинна. ${\displaystyle A_{1},\ldots ,A_{n}}$ ${\displaystyle \neg B}$ ${\displaystyle \neg B}$

С технической точки зрения, методы модальных таблиц проверяют существование модели и мира , которые делают набор формул истинным. Если они верны в , то должен существовать мир , доступный из которого и который делает их истинными. Таким образом, это правило сводится к выводу набора формул, которым должны удовлетворяться такие . ${\displaystyle M}$ ${\displaystyle w}$ ${\displaystyle \Box A_{1};\ldots ;\Box A_{n};\neg \Box B}$ ${\displaystyle w}$ ${\displaystyle w'}$ ${\displaystyle w}$ ${\displaystyle A_{1};\ldots ;A_{n};\neg B}$ ${\displaystyle w'}$

В то время как предварительные условия считаются удовлетворенными , последствия считаются удовлетворенными в : той же модели, но, возможно, в разных мирах. Таблицы с метками множества не отслеживают явным образом мир, в котором каждая формула считается истинной: два узла могут относиться или не относиться к одному и тому же миру. Однако формулы, обозначающие любой данный узел, считаются верными в том же мире. ${\displaystyle \Box A_{1};\ldots ;\Box A_{n};\neg \Box B}$ ${\displaystyle M,w}$ ${\displaystyle A_{1};\ldots ;A_{n};\neg B}$ ${\displaystyle M,w'}$

В результате возможного существования разных миров, в которых формулы считаются истинными, формула в узле не является автоматически допустимой для всех ее потомков, поскольку каждое применение модального правила соответствует переходу из одного мира в другой. Это условие автоматически фиксируется таблицами маркировки наборов, поскольку правила расширения основаны только на листе, к которому они применяются, а не на его предках.

Примечательно, что это не распространяется напрямую на несколько отрицательных формул в рамке, таких как : хотя существует доступный мир, в котором ложно, и мир, в котором ложно, эти два мира не обязательно одинаковы. ${\displaystyle (K)}$ ${\displaystyle \Box A_{1};\ldots ;\Box A_{n};\neg \Box B_{1};\neg \Box B_{2}}$ ${\displaystyle B_{1}}$ ${\displaystyle B_{2}}$

В отличие от пропозициональных правил, условия формулируются поверх всех своих предусловий. Например, его нельзя применить к узлу, помеченному ; хотя этот набор несовместен и это можно легко доказать, применив , это правило не может быть применено из-за формулы , которая даже не имеет отношения к несогласованности. Удаление таких формул возможно по правилу: ${\displaystyle (K)}$ ${\displaystyle a;\Box b;\Box (b\rightarrow c);\neg \Box c}$ ${\displaystyle (K)}$ ${\displaystyle a}$

${\displaystyle (\theta ){\frac {A_{1};\ldots ;A_{n};B_{1};\ldots ;B_{m}}{A_{1};\ldots ;A_{n}}}}$

Добавление этого правила (правила прореживания) делает полученное исчисление неслитным: таблицу для противоречивого набора может быть невозможно закрыть, даже если закрытая таблица для того же набора существует.

Правило недетерминировано: набор формул, которые нужно удалить (или сохранить), можно выбрать произвольно; это создает проблему выбора набора формул для отбрасывания, который не настолько велик, чтобы сделать результирующий набор выполнимым, и не настолько мал, чтобы сделать необходимые правила расширения неприменимыми. Наличие большого количества возможных вариантов усложняет задачу поиска закрытой таблицы. ${\displaystyle (\theta )}$

Этого недетерминизма можно избежать, ограничив использование так, чтобы оно применялось только перед правилом модального расширения и чтобы оно удаляло только формулы, которые делают это другое правило неприменимым. Это условие также можно сформулировать путем объединения двух правил в одно. Полученное правило дает тот же результат, что и старое, но неявно отбрасывает все формулы, которые делали старое правило неприменимым. Доказано, что этот механизм удаления сохраняет полноту для многих модальных логик. ${\displaystyle (\theta )}$ ${\displaystyle (\theta )}$

Аксиома Т выражает рефлексивность отношения доступности: каждый мир доступен сам по себе. Соответствующее правило расширения таблицы:

${\displaystyle (T){\frac {A_{1};\ldots ;A_{n};\Box B}{A_{1};\ldots ;A_{n};\Box B;B}}}$

Это правило связывает условия в одном и том же мире: если оно истинно в каком-то мире, то в силу рефлексивности оно также истинно и в том же мире . Это правило является статическим, а не транзакционным, поскольку и его предварительное условие, и последующее относятся к одному и тому же миру. ${\displaystyle \Box B}$ ${\displaystyle B}$

Это правило копирует предусловие в последующее, несмотря на то, что эта формула «использовалась» для генерации . Это верно, поскольку рассматриваемый мир один и тот же, поэтому и там сохраняется. Такое «копирование» необходимо в некоторых случаях. Например, необходимо доказать несостоятельность : единственные применимые правила - в порядке , из которых одно блокируется, если не скопировано. ${\displaystyle \Box B}$ ${\displaystyle B}$ ${\displaystyle \Box B}$ ${\displaystyle \Box (a\wedge \neg \Box a)}$ ${\displaystyle (T),(\wedge ),(\theta ),(K)}$ ${\displaystyle \Box a}$

Вспомогательные таблицы

Другой метод работы с формулами, содержащимися в альтернативных мирах, заключается в создании новой таблицы для каждого нового мира, который вводится в таблицу. Например, подразумевается, что это ложно в доступном мире, поэтому начинается новая таблица, корнем которой является . Эта новая таблица прикрепляется к узлу исходной таблицы, к которому было применено правило расширения; закрытие этой таблицы немедленно порождает закрытие всех ветвей, где находится этот узел, независимо от того, связаны ли с этим же узлом другие вспомогательные таблицы. Правила раскрытия вспомогательных таблиц такие же, как и для исходной; следовательно, вспомогательная таблица может, в свою очередь, иметь другие (под)вспомогательные таблицы. ${\displaystyle \neg \Box A}$ ${\displaystyle A}$ ${\displaystyle \neg A}$

Глобальные предположения

Приведенные выше модальные таблицы устанавливают согласованность набора формул и могут использоваться для решения локальной проблемы логических следствий . Это проблема определения того, является ли для каждой модели истинной в определенном мире то , что она истинна и в том же мире. Это то же самое, что проверять, верно ли предположение в мире той же модели, которое верно и в том же мире той же модели. ${\displaystyle M}$ ${\displaystyle A}$ ${\displaystyle w}$ ${\displaystyle B}$ ${\displaystyle B}$ ${\displaystyle A}$

Связанная с этим проблема — это проблема глобальных последствий, когда предполагается, что формула (или набор формул) верна во всех возможных мирах модели. Проблема состоит в том, чтобы проверить, верно ли во всех мирах то , что истинно во всех мирах. ${\displaystyle G}$ ${\displaystyle M}$ ${\displaystyle G}$ ${\displaystyle B}$

Локальные и глобальные предположения различаются в моделях, где предполагаемая формула верна в одних мирах, но не верна в других. Например, влечет за собой глобальный, но не локальный характер. Локальное следствие не выполняется в модели, состоящей из двух миров, создающих и истинных соответственно, и где второй доступен из первого; в первом мире предположения верны, но ложны. Этот контрпример работает, потому что его можно считать истинным в одном мире и ложным в другом. Однако если одно и то же предположение считается глобальным, оно не допускается ни в одном мире модели. ${\displaystyle \{P,\neg \Box (P\wedge Q)\}}$ ${\displaystyle \neg \Box Q}$ ${\displaystyle P}$ ${\displaystyle \neg P,Q}$ ${\displaystyle \neg \Box Q}$ ${\displaystyle P}$ ${\displaystyle \neg P}$

Эти две проблемы можно объединить, чтобы можно было проверить, является ли локальным следствием глобального предположения . Табличные исчисления могут обрабатывать глобальные предположения с помощью правила, позволяющего добавлять их к каждому узлу, независимо от мира, к которому оно относится. ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle G}$

Обозначения

Иногда используются следующие соглашения.

Единые обозначения

При написании правил расширения таблиц формулы часто обозначаются с использованием соглашения, так что, например, всегда считается . В следующей таблице представлены обозначения формул в пропозициональной логике, логике первого порядка и модальной логике. ${\displaystyle \alpha }$ ${\displaystyle \alpha _{1}\wedge \alpha _{2}}$

Каждая метка в первом столбце принимается за любую формулу в других столбцах. Перечеркнутая формула, такая как указывает, что является отрицанием любой формулы, появляющейся на ее месте, так что, например, в формуле подформула является отрицанием . ${\displaystyle {\overline {\alpha _{1}}}}$ ${\displaystyle \alpha _{1}}$ ${\displaystyle \neg (a\vee b)}$ ${\displaystyle \alpha _{1}}$ ${\displaystyle a}$

Поскольку каждая метка указывает на множество эквивалентных формул, такое обозначение позволяет написать одно правило для всех этих эквивалентных формул. Например, правило расширения конъюнкции формулируется так:

${\displaystyle (\alpha ){\frac {\alpha }{\begin{array}{c}\alpha _{1}\\\alpha _{2}\end{array}}}}$

Формулы со знаком

Формула в таблице считается истинной. Таблицы со знаком позволяют утверждать, что формула неверна. Обычно это достигается путем добавления метки к каждой формуле, где метка T указывает на формулы, которые считаются истинными, а F — на ложные. Другое, но эквивалентное обозначение заключается в записи формул, которые считаются истинными слева от узла, и формул, которые считаются ложными, справа.

Смотрите также

• Разрешение (логика)

Примечания

1. Хаусон, Колин (1997). Логика с деревьями: введение в символическую логику . Лондон; Нью-Йорк: Рутледж. стр. ix, x, 24–29, 47. ISBN. 978-0-415-13342-5.
2. Ресталл, Грег (2006). Логика: введение. Основы философии. Лондон; Нью-Йорк: Рутледж. стр. 5, 42, 55. ISBN. 978-0-415-40067-1. ОСЛК  63115330.
3. Хаусон 2005, с. 27.
4. Девушка 2014.
5. Энциклопедия философии 2023.
6. Бет 1955.
7. Смуллян 1995.
8. Карниелли 1987.
9. Карниелли 1991.
10. Платон, Ян фон (2013). Элементы логических рассуждений (1. изд.). Кембридж: Издательство Кембриджского университета. п. 9. ISBN 978-1-107-03659-8.
11. Вайсштейн, Эрик В. «Соединительный». mathworld.wolfram.com . Проверено 22 марта 2024 г.
12. Вариант этого начального шага — начать с дерева с одним узлом, корень которого помечен значком . Во втором случае процедура всегда может скопировать формулу из набора под листом. В качестве рабочего примера показана таблица для набора . ${\displaystyle \top }$ ${\displaystyle \{(a\vee \neg b)\wedge b,\neg a\}}$
13. Применимый узел — это узел , самая внешняя связка которого соответствует правилу расширения и который еще не применялся ни на одном предыдущем узле в ветви выбранного листового узла.
14. Смуллян 2014, стр. 88–89.

Рекомендации

• Бет, Эверт В. (1955). «Семантическая следствие и формальная выводимость». Mededelingen van de Koninklijke Nederlandse Akademie van Wetenschappen, Afdeling Letterkunde . 18 (13): 309–42.Перепечатано в Intikka, Jaakko, изд. (1969). Философия математики . Издательство Оксфордского университета. ISBN 978-0-19-875011-6.
• Босток, Дэвид (1997). Промежуточная логика. Издательство Оксфордского университета. ISBN 978-0-19-156707-0.
• Карниелли, Уолтер А. (1987). «Систематизация конечной многозначной логики методом таблиц». Журнал символической логики . 52 (2): 473–493. дои : 10.2307/2274395. JSTOR  2274395. S2CID  42822367.
• Карниелли, Уолтер А. (1991). «О секвенциях и таблицах многозначной логики» (PDF) . Журнал неклассической логики . 8 (1): 59–76. Архивировано из оригинала (PDF) 5 марта 2016 г. Проверено 11 октября 2014 г.
• Д'Агостино, М.; Габбай, Д .; Хенле, Р.; Посегга, Дж., ред. (1999). Справочник по табличным методам. Клювер. ISBN 978-94-017-1754-0.
• Фиттинг, Мелвин (1996) [1990]. Логика первого порядка и автоматическое доказательство теорем (2-е изд.). Нью-Йорк: Спрингер. дои : 10.1007/978-1-4612-2360-3. ISBN 978-1-4612-7515-2. S2CID  10411039.
• Гирле, Род (2014). Модальная логика и философия (2-е изд.). Тейлор и Фрэнсис. ISBN 978-1-317-49217-7.
• Горе, Раджив. «Табличные методы для модальной и темпоральной логики». Справочник по табличным методам . стр. 297–396.
• Хэнле, Райнер (2001). «3. Таблицы и связанные с ними методы». В Робинсоне, Алан Дж.А.; Воронков, Андрей (ред.). Справочник по автоматизированному рассуждению . Эльзевир. стр. 101–179. ISBN 978-0-08-053279-0.
• Хаусон, Колин (11 октября 2005 г.) [1997]. Логика с деревьями: введение в символическую логику. Рутледж. ISBN 978-1-134-78550-6.
• Джеффри, Ричард (2006) [1967]. Формальная логика: ее объем и пределы (4-е изд.). Хакетт. ISBN 978-0-87220-813-1.
• Летц, Рейнхольд; Стенц, Гернот. «28. Процедуры исключения модели и таблицы соединений». Справочник по автоматизированному рассуждению . стр. 2015–2114 гг.
• Смалльян, Раймонд (1995) [1968]. Логика первого порядка. Дувр. ISBN 978-0-486-68370-6.
• Смуллян, Раймонд (2014). Руководство для начинающих по математической логике . Дувр. ISBN 978-0486492377.
• Энциклопедия философии, изд. (11 декабря 2023 г.). «Современная логика: логический период: Кэрролл». Энциклопедия философии . Проверено 26 декабря 2023 г.
• Земан, Джозеф Джей (1973). Модальная логика: модальные системы Льюиса. Кларендон Пресс. ISBN 978-0-19-824374-8. ОСЛК  641504.

Внешние ссылки

• TABLEAUX: ежегодная международная конференция по автоматизированному рассуждению с помощью аналитических таблиц и связанных с ними методов.
• JAR: Журнал автоматизированного рассуждения
• Пакет tableaux: интерактивное средство доказательства пропозициональной логики и логики первого порядка с использованием таблиц.
• Генератор доказательств дерева: еще одно интерактивное средство доказательства для логики высказываний и логики первого порядка с использованием таблиц.
• LoTREC: универсальное средство доказательства модальной логики на основе таблиц от IRIT/Тулузского университета.
• Знакомство с деревьями истины на YouTube