Timsort — это гибридный , стабильный алгоритм сортировки , полученный из сортировки слиянием и сортировки вставкой , разработанный для хорошей работы со многими типами реальных данных. Он был реализован Тимом Питерсом в 2002 году для использования в языке программирования Python . Алгоритм находит подпоследовательности данных, которые уже упорядочены (прогоны), и использует их для более эффективной сортировки остатка. Это делается путем слияния прогонов до тех пор, пока не будут выполнены определенные критерии. Timsort является стандартным алгоритмом сортировки Python с версии 2.3 (с версии 3.11 с использованием политики слияния Powersort [5] ), и используется для сортировки массивов непримитивного типа в Java SE 7 , [6] на платформе Android , [7] в GNU Octave , [8] на V8 , [9] Swift , [10] и вдохновил алгоритм сортировки, используемый в Rust . [11]
Он использует методы из статьи Питера Макилроя 1993 года «Оптимистическая сортировка и теоретическая сложность информации». [12]
Timsort был разработан для использования преимуществ серий последовательных упорядоченных элементов, которые уже существуют в большинстве реальных данных, естественных серий . Он выполняет итерации по данным, собирая элементы в серии и одновременно помещая эти серии в стек. Всякий раз, когда серии наверху стека соответствуют критерию слияния, они объединяются. Это продолжается до тех пор, пока все данные не будут пройдены; затем все серии объединяются по две за раз, и остается только одна отсортированная серия. Преимущество объединения упорядоченных серий вместо объединения подсписков фиксированного размера (как это делается традиционной сортировкой слиянием) заключается в том, что это уменьшает общее количество сравнений, необходимых для сортировки всего списка.
Каждый запуск имеет минимальный размер, который основан на размере входных данных и определяется в начале алгоритма. Если запуск меньше этого минимального размера запуска, сортировка вставкой используется для добавления дополнительных элементов в запуск, пока не будет достигнут минимальный размер запуска.

Timsort — это стабильный алгоритм сортировки (сохраняется порядок элементов с одинаковым ключом), который стремится выполнять сбалансированные слияния (таким образом, слияние объединяет серии схожих размеров).
Для достижения стабильности сортировки объединяются только последовательные прогоны. Между двумя непоследовательными прогонами может быть элемент с одинаковым ключом внутри прогонов. Объединение этих двух прогонов изменит порядок равных ключей. Пример такой ситуации ([] — упорядоченные прогоны): [1 2 2] 1 4 2 [0 1 2]
В поисках сбалансированных слияний Timsort рассматривает три прохода на вершине стека, X , Y , Z , и сохраняет инварианты:
Если какой-либо из этих инвариантов нарушается, Y объединяется с меньшим из X или Z , и инварианты проверяются снова. Как только инварианты соблюдаются, можно начинать поиск нового запуска в данных. [14] Эти инварианты поддерживают слияния как приблизительно сбалансированные, поддерживая компромисс между задержкой слияния для баланса, использованием новых вхождений запусков в кэш-память и относительно простым принятием решений о слиянии.
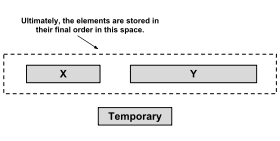
Исходная реализация сортировки слиянием не является in-place и имеет накладные расходы пространства N (размер данных). Реализации сортировки слиянием in-place существуют, но имеют высокие накладные расходы времени. Для достижения среднего термина Timsort выполняет сортировку слиянием с небольшими накладными расходами времени и меньшими накладными расходами пространства, чем N.
Сначала Timsort выполняет бинарный поиск , чтобы найти место, где первый элемент второго запуска будет вставлен в первый упорядоченный запуск, сохраняя его упорядоченным. Затем он выполняет тот же алгоритм, чтобы найти место, где последний элемент первого запуска будет вставлен во второй упорядоченный запуск, сохраняя его упорядоченным. Элементы до и после этих мест уже находятся на своих правильных местах и не нуждаются в объединении. Затем меньший из этих сокращенных запусков копируется во временную память, а скопированные элементы объединяются с большим сокращенным запуском в теперь свободное пространство. Если самый левый сокращенный запуск меньше, объединение продолжается слева направо. Если самый правый сокращенный запуск меньше, объединение продолжается справа налево (т. е. начинается с элементов на концах временного пространства и самого левого запуска и заполняется свободное пространство с его конца). Эта оптимизация уменьшает количество требуемых перемещений элементов, время выполнения и накладные расходы на временное пространство в общем случае.
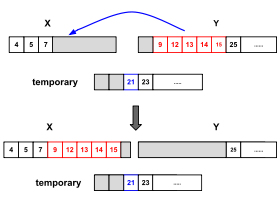
Пример: необходимо объединить два прогона [1, 2, 3, 6, 10] и [4, 5, 7, 9, 12, 14, 17]. Обратите внимание, что оба прогона уже отсортированы по отдельности. Наименьший элемент второго прогона — 4, и его нужно добавить на четвертую позицию первого прогона, чтобы сохранить его порядок (предполагая, что первая позиция прогона — 1). Наибольший элемент первого прогона — 10, и его нужно добавить на пятую позицию второго прогона, чтобы сохранить его порядок. Таким образом, [1, 2, 3] и [12, 14, 17] уже находятся в своих конечных позициях, а прогоны, в которых требуется перемещение элементов, — [6, 10] и [4, 5, 7, 9]. Зная это, нам нужно только выделить временный буфер размером 2 вместо 4.
Слияние может выполняться в обоих направлениях: слева направо, как при традиционной сортировке слиянием, или справа налево.

Индивидуальное слияние запусков R1 и R2 сохраняет количество последовательных элементов, выбранных из запуска. Когда это число достигает минимального порога галопирования ( min_gallop ), Timsort считает, что, вероятно, из этого запуска все еще может быть выбрано много последовательных элементов, и переключается в режим галопирования. Предположим, что за его запуск отвечает R1. В этом режиме алгоритм выполняет двухэтапный поиск места в запуске R1, куда будет вставлен следующий элемент x запуска R2. На первом этапе он выполняет экспоненциальный поиск , также известный как галопирующий поиск, пока не найдет k, такой что R1[2 k−1 − 1] < x <= R1[2 k − 1], т. е. область неопределенности, включающую 2 k−1 − 1 последовательных элементов R1. На втором этапе выполняется прямой двоичный поиск этой области, чтобы найти точное местоположение в R1 для x . Режим галопирования — это попытка адаптировать алгоритм слияния к шаблону интервалов между элементами в сериях.
Галопирование не всегда эффективно. В некоторых случаях галопирующий режим требует больше сравнений, чем простой линейный поиск . Согласно тестам, проведенным разработчиком, галопирование выгодно только тогда, когда начальный элемент одного запуска не является одним из первых семи элементов другого запуска. Это подразумевает начальный порог 7. Чтобы избежать недостатков галопирующего режима, предпринимаются два действия: (1) Когда галопирование оказывается менее эффективным, чем бинарный поиск , галопирующий режим выходит. (2) Успех или неудача галопирования используется для корректировки min_gallop . Если выбранный элемент находится в том же массиве, который ранее возвращал элемент, min_gallop уменьшается на единицу, тем самым поощряя возврат в галопирующий режим. В противном случае значение увеличивается на единицу, тем самым препятствуя возврату в галопирующий режим. В случае случайных данных значение min_gallop становится настолько большим, что галопирующий режим никогда не повторяется. [15]
Чтобы также воспользоваться данными, отсортированными по убыванию, Timsort переворачивает строго нисходящие прогоны, когда находит их, и добавляет их в стек прогонов. Поскольку нисходящие прогоны позже слепо переворачиваются, исключение прогонов с равными элементами сохраняет устойчивость алгоритма; т. е. равные элементы не будут переворачиваться.
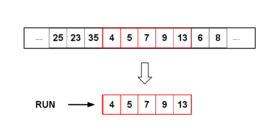
Поскольку слияние наиболее эффективно, когда количество запусков равно или немного меньше степени двойки, и заметно менее эффективно, когда количество запусков немного больше степени двойки, Timsort выбирает minrun , чтобы попытаться обеспечить первое условие. [13]
Minrun выбирается из диапазона от 32 до 64 включительно, так что размер данных, деленный на minrun , равен или немного меньше степени двойки. Окончательный алгоритм берет шесть самых значимых бит размера массива, добавляет один, если любой из оставшихся битов установлен, и использует этот результат как minrun . Этот алгоритм работает для всех массивов, включая те, которые меньше 64; для массивов размером 63 или меньше это устанавливает minrun равным размеру массива, и Timsort сводится к сортировке вставкой. [13]
В худшем случае Timsort использует сравнения для сортировки массива из n элементов. В лучшем случае, когда входные данные уже отсортированы, он работает за линейное время, что означает, что это адаптивный алгоритм сортировки . [3]
Он превосходит быструю сортировку для сортировки ссылок на объекты или указателей, поскольку для доступа к данным и выполнения сравнений требуется дорогостоящее косвенное обращение к памяти, а преимущества быстрой сортировки в плане когерентности кэша значительно снижаются.
В 2015 году голландские и немецкие исследователи в проекте EU FP7 ENVISAGE обнаружили ошибку в стандартной реализации Timsort. [16] Она была исправлена в 2015 году в Python, Java и Android.
В частности, инварианты размеров стекированных запусков обеспечивают узкую верхнюю границу максимального размера требуемого стека. Реализация предварительно выделила стек, достаточный для сортировки 2 64 байт входных данных, и избежала дальнейших проверок переполнения.
Однако гарантия требует, чтобы инварианты применялись к каждой группе из трех последовательных запусков, но реализация проверяла это только для первых трех. [16] Используя инструмент KeY для формальной проверки программного обеспечения Java, исследователи обнаружили, что этой проверки недостаточно, и им удалось найти длины запусков (и входные данные, которые генерировали эти длины запусков), которые привели бы к нарушению инвариантов глубже в стеке после объединения вершины стека. [17]
В результате для некоторых входов выделенный размер недостаточен для хранения всех не объединенных запусков. В Java это создает для этих входов исключение выхода за пределы массива. Наименьший вход, который вызывает это исключение в Java и Android v7, имеет размер67 108 864 (2 26 ). (Старые версии Android уже вызывали это исключение для определенных входных данных размером65 536 (2 16 ))
Реализация Java была исправлена путем увеличения размера предварительно выделенного стека на основе обновленного анализа наихудшего случая. В статье также было показано формальными методами, как установить предполагаемый инвариант, проверив, что четыре верхних запуска в стеке удовлетворяют двум правилам выше. Этот подход был первоначально принят Python [18] , пока он не перешел на Powersort в 2022 году с выпуском Python 3.11. [5]
Timsort] также имеет хорошие аспекты: он стабилен (элементы, которые сравниваются как равные, сохраняют свой относительный порядок, поэтому, например, если вы сначала сортируете по почтовому индексу, а затем по имени, люди с одинаковыми именами все равно отображаются в порядке увеличения почтового индекса; это важно в приложениях, которые, например, уточняют результаты запросов на основе ввода пользователя). ... Он не имеет плохих случаев (O(N log N) — худший случай; N−1 сравнений — лучший).
TimSort — это интригующий алгоритм сортировки, разработанный в 2002 г. для Python, сложность которого в наихудшем случае была объявлена, но не доказана до нашего недавнего препринта.
в значительной степени украден из Python, listobject.c, который сам по себе не имел заголовка лицензии. Тем не менее, спасибо Тиму Питерсу за части кода, которые я украл.
Текущий алгоритм представляет собой адаптивную итеративную сортировку слиянием, вдохновленную timsort. Он разработан так, чтобы быть очень быстрым в случаях, когда срез почти отсортирован или состоит из двух или более отсортированных последовательностей, соединенных одна за другой.