
В комбинаторной математике тор Де Брейна , названный в честь голландского математика Николаса Говерта де Брейна , представляет собой массив символов из алфавита (часто просто 0 и 1), содержащий каждую возможную матрицу заданных размеров m × n ровно один раз. Это тор, потому что ребра считаются обертывающими с целью нахождения матриц. Его название происходит от последовательности Де Брейна , которую можно считать особым случаем, когда n = 1 (одно измерение).
Один из главных открытых вопросов относительно торов Де Брейна заключается в том, можно ли построить тор Де Брейна для определенного размера алфавита для заданных m и n . Известно, что они всегда существуют при n = 1 , поскольку тогда мы просто получаем последовательности Де Брейна, которые всегда существуют. Также известно, что «квадратные» торы существуют, когда m = n и четно (для нечетного случая полученные торы не могут быть квадратными). [1] [2] [3]
Наименьший возможный бинарный «квадратный» тор де Брейна, изображенный справа вверху, обозначаемый как (4,4;2,2) 2 тор де Брейна (или просто как B 2 ), содержит все бинарные матрицы 2×2 .

За исключением «трансляции», «инверсии» (перестановки нулей и единиц) и «вращения» (на 90 градусов), никакие другие (4,4;2,2) 2 тора де Брейна невозможны – это можно показать путем полного просмотра всех 2 16 двоичных матриц (или подмножества, удовлетворяющего ограничениям, таким как равное количество нулей и единиц). [4]

Тор можно развернуть, повторяя n −1 строк и столбцов. Все n × n подматрицы без обертывания, такие как закрашенная желтым, затем образуют полный набор:

Пример следующего возможного бинарного «квадратного» тора де Брейна, (256,256;4,4) 2 (сокращенно B 4 ), был явно построен. [5]
На изображении справа показан пример тора/массива де Брейна (256,256;4,4) 2 , где нули закодированы как белые, а единицы — как красные пиксели соответственно.
Статья, в которой был построен пример тора де Брейна (256,256;4,4) 2 , содержала более 10 страниц двоичного текста, несмотря на уменьшенный размер шрифта, требующий трех строк на строку массива.
Последующий возможный двоичный тор де Брейна, содержащий все двоичные матрицы 6×6 , имел бы 2 36 = 68 719 476 736 записей, что дало бы квадратный массив размерностью 262 144 × 262 144 , обозначаемый как (262144,262144;6,6) 2 тор де Брейна или просто B 6 . Это можно было бы легко сохранить на компьютере — если бы оно было напечатано пикселями со стороной 0,1 мм, такая матрица потребовала бы площади приблизительно 26 × 26 квадратных метров .
Объект B 8 , содержащий все бинарные матрицы 8×8 и обозначенный (4294967296,4294967296;8,8) 2 , имеет в общей сложности 2 64 ≈ 18.447×10 18 записей: для хранения такой матрицы потребуется 18.5 экзабит или 2.3 экзабайт памяти. В указанном выше масштабе он покроет 429×429 квадратных километров .
Следующая таблица иллюстрирует сверхэкспоненциальный рост.
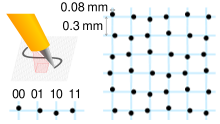
Торы Де Брейна используются в контексте пространственного кодирования, например, для локализации камеры [6] , робота [7] или материального объекта [8] на основе некоторого оптического рисунка земли.
Они также используются в качестве основы PuzzleBoard [9] , оптической калибровочной мишени камеры, которая добавляет кодировку положения к шаблону калибровки шахматной доски. [10]
Торы Де Брейна могут быть использованы для реализации цифровой бумаги , подобно системе Anoto . Однако каждая ячейка Anoto имеет четыре возможных состояния вместо двух в торах Де Брейна. Он также использует повторяющуюся 6-битную последовательность Де Брейна с различными смещениями в качестве столбцов. [11]