Цветовое пространство CIE 1931

В 1931 году Международная комиссия по освещению (CIE) опубликовала цветовые пространства CIE 1931 , которые определяют связь между видимым спектром и зрительным восприятием определенных цветов человеческим цветовым зрением . ^[1]^[2] Цветовые пространства CIE представляют собой математические модели, которые создают «стандартного наблюдателя», который пытается предсказать восприятие уникальных оттенков цвета. Эти цветовые пространства являются важными инструментами, которые обеспечивают основу для измерения цвета в промышленности, включая чернила, красители и краски, освещение, цветное изображение и т. д. Цветовые пространства CIE способствовали развитию цветного телевидения, созданию инструментов для поддержания постоянного цвета в производственных процессах и других методов управления цветом .

Аббревиатура CIE происходит от французского названия «Commission Internationale de l'éclairage» , которая поддерживала и развивала многие из используемых сегодня стандартов, связанных с колориметрией . Цветовые пространства CIE были созданы с использованием данных из серии экспериментов, в которых испытуемые люди корректировали основные цвета красного, зеленого и синего, чтобы найти визуальное соответствие второму, чистому цвету. Первоначальные эксперименты были проведены в середине 1920-х годов Уильямом Дэвидом Райтом с использованием десяти наблюдателей ^[3] и Джоном Гилдом с использованием семи наблюдателей ^[4] . Экспериментальные результаты были объединены, создав цветовое пространство CIE RGB. Цветовое пространство CIE XYZ было получено из CIE RGB в попытке упростить математику.

Цветовое пространство CIE 1931 XYZ по-прежнему широко используется, хотя оно не является перцептивно однородным по отношению к человеческому зрению. В 1976 году CIE опубликовала цветовые пространства CIELUV и CIELAB , которые являются производными от XYZ и предназначены для предоставления более однородных прогнозов относительно человеческого восприятия.

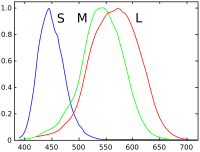
Предыстория: человеческий глаз и трехцветные значения

Человеческий глаз с нормальным зрением имеет три вида колбочек , которые воспринимают свет, имея пики спектральной чувствительности в коротких («S», 420 нм – 440 нм ), средних («M», 530 нм – 540 нм ) и длинных («L», 560 нм – 580 нм ) длинах волн. Эти колбочки лежат в основе восприятия цвета человеком в условиях средней и высокой яркости; при очень тусклом свете цветовое зрение ухудшается, и становятся эффективными низкояркие, монохроматические рецепторы «ночного видения», называемые « палочками ». Таким образом, три параметра, соответствующие уровням стимула трех видов колбочек, в принципе описывают любое цветовое ощущение человека. Взвешивание общего спектра мощности света с помощью индивидуальной спектральной чувствительности трех видов колбочек дает три эффективных значения стимула ; эти три значения составляют трехстимульную спецификацию объективного цвета светового спектра. Три параметра, обозначенные «S», «M» и «L», указываются с использованием трехмерного пространства, называемого « цветовым пространством LMS », которое является одним из многих цветовых пространств, разработанных для количественной оценки цветового зрения человека .

Цветовое пространство отображает диапазон физически созданных цветов из смешанного света, пигментов и т. д. в объективное описание цветовых ощущений, регистрируемых человеческим глазом, как правило, в терминах трехцветных значений, но обычно не в цветовом пространстве LMS, определяемом спектральной чувствительностью колбочек . Трехцветные значения , связанные с цветовым пространством, можно концептуализировать как суммы трех основных цветов в трехцветной аддитивной цветовой модели . В некоторых цветовых пространствах, включая пространства LMS и XYZ, используемые основные цвета не являются реальными цветами в том смысле, что они не могут быть созданы ни в каком световом спектре.

Цветовое пространство CIE XYZ охватывает все цветовые ощущения, которые видит человек со средним зрением. Вот почему трехцветные значения CIE XYZ являются инвариантным к устройству представлением цвета. ^[5] Оно служит стандартным эталоном, относительно которого определяются многие другие цветовые пространства. Набор функций сопоставления цветов, таких как кривые спектральной чувствительности цветового пространства LMS , но не ограничиваясь неотрицательными чувствительностью, связывает физически произведенные световые спектры с определенными трехцветными значениями.

Рассмотрим два источника света, составленных из различных смесей волн разной длины. Такие источники света могут казаться одного цвета; этот эффект называется « метамерией ». Такие источники света имеют одинаковый видимый цвет для наблюдателя, когда они создают одинаковые тристимульные значения, независимо от спектрального распределения мощности источников.

Большинство длин волн стимулируют два или все три типа колбочек , поскольку кривые спектральной чувствительности трех типов перекрываются. Таким образом, некоторые трехцветные значения физически невозможны: например, трехцветные значения LMS, которые не равны нулю для компонента M и равны нулю для компонентов L и S. Кроме того, чистые спектральные цвета в любом нормальном трихроматическом аддитивном цветовом пространстве, например, цветовых пространствах RGB , подразумевали бы отрицательные значения по крайней мере для одного из трех основных цветов , поскольку цветность находилась бы за пределами цветового треугольника, определяемого основными цветами. Чтобы избежать этих отрицательных значений RGB и иметь один компонент, описывающий воспринимаемую яркость , были сформулированы «мнимые» основные цвета и соответствующие функции сопоставления цветов. Цветовое пространство CIE 1931 определяет результирующие трехцветные значения, в которых они обозначены как «X», «Y» и «Z». ^[6] В пространстве XYZ все комбинации неотрицательных координат имеют смысл, но многие из них, такие как основные местоположения [1, 0, 0], [0, 1, 0] и [0, 0, 1], соответствуют воображаемым цветам за пределами пространства возможных координат LMS; воображаемые цвета не соответствуют никакому спектральному распределению длин волн и, следовательно, не имеют физической реальности.

ЗначениеХ,ИиЗ

В модели CIE 1931 Y — это яркость , Z почти равно синему (CIE RGB), а X — это смесь трех кривых CIE RGB, выбранных неотрицательными (см. § Определение цветового пространства CIE XYZ). Установка Y в качестве яркости имеет полезный результат: для любого заданного значения Y плоскость XZ будет содержать все возможные цветности при этой яркости.

Единица измерения трехцветных значений $X$ , $Y$ и $Z$ часто выбирается произвольно, так что $Y = 1$ или $Y = 100$ — это самый яркий белый цвет, поддерживаемый цветным дисплеем. В этом случае значение Y известно как относительная яркость . Соответствующие значения белой точки для $X$ и $Z$ затем могут быть выведены с использованием стандартных источников света .

Поскольку значения XYZ были определены гораздо раньше, чем характеристика колбочек в 1950-х годах ( Рагнаром Гранитом ), ^[7] физиологическое значение этих значений стало известно гораздо позже. Матрица Ханта-Пойнтера-Эстевеса из 1980-х годов связывает XYZ с LMS. ^[8] При инвертировании она показывает, как три ответа колбочек складываются в функции XYZ:

{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}=\left[{\begin{aligned}1&.910\,20\!\!\!&\!\!-1&.112\,12\!\!\!&\!\!0&.201\,91\\0&.370\,95\!\!\!&\!\!0&.629\,05\!\!\!&\!\!0&\\0&\!\!&\!\!0&\!\!\!&\!\!1&.000\,00\end{aligned}}\right]{\begin{bmatrix}L\\M\\S\end{bmatrix}}_{\rm {HPE}}

Другими словами, значение Z состоит исключительно из ответа колбочки S, значение Y — из смеси ответов L и M, а значение X — из смеси всех трех. Этот факт делает значения XYZ аналогичными ответам колбочки LMS человеческого глаза, но отличными от них.

наблюдатель стандарта CIE

Из-за распределения колбочек в глазу значения трехстимула зависят от поля зрения наблюдателя . Чтобы устранить эту переменную, CIE определила функцию цветового картирования, называемую стандартным (колориметрическим) наблюдателем , для представления средней хроматической реакции человека в пределах дуги 2° внутри фовеа . Этот угол был выбран из-за убеждения, что цветочувствительные колбочки находятся в пределах дуги 2° фовеа. Таким образом, функция CIE 1931 Standard Observer также известна как CIE 1931 2° Standard Observer . Более современной, но менее используемой альтернативой является CIE 1964 10° Standard Observer , которая получена из работы Стайлза и Берча ^[9] и Сперанской. ^[10]

Для экспериментов с углом 10° наблюдателям было поручено игнорировать центральное пятно 2°. Функция дополнительного стандартного наблюдателя 1964 года рекомендуется при работе с полем зрения более 4°. Обе стандартные функции наблюдателя дискретизируются на интервалах длин волн 5 нм от 380 нм до 780 нм и распределяются CIE . ^[11] Все соответствующие значения были рассчитаны на основе экспериментально полученных данных с использованием интерполяции . Стандартный наблюдатель характеризуется тремя функциями сопоставления цветов .

Существует также набор данных с интервалом 1 нм для CIE 1931 и CIE 1964, предоставленный Вышецким в 1982 году. ^[12] В публикации CIE за 1986 год также, по-видимому, имеется набор данных с интервалом 1 нм, вероятно, использующий те же данные. ^[13] Как и обычный набор данных с интервалом 5 нм , этот набор данных также получен путем интерполяции.

Вывод стандартного наблюдателя CIE из экспериментов по сопоставлению цветов приведен ниже после описания пространства CIE RGB.

Функции сопоставления цветов

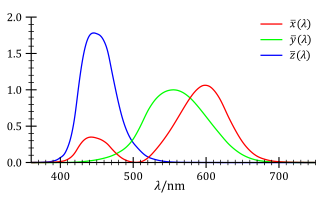
Функции цветового соответствия CIE и являются числовым описанием хроматической реакции наблюдателя ( описанной выше). Их можно рассматривать как спектральные кривые чувствительности трех линейных детекторов света, дающие трехцветные значения CIE X , Y и Z. В совокупности эти три функции описывают стандартного наблюдателя CIE. ^[14] ${\overline {x}}(\лямбда)$ ${\overline {y}}(\лямбда)$ ${\overline {z}}(\lambda )$

Аналитическое приближение

Поиск по таблице может стать непрактичным для некоторых вычислительных задач. Вместо того, чтобы ссылаться на опубликованную таблицу, функции сопоставления цветов CIE XYZ могут быть аппроксимированы суммой гауссовых функций следующим образом: ^[15]

Пусть g ( x ) обозначает кусочно-гауссову функцию, определяемую формулой

g(x;\mu ,\tau _{1},\tau _{2})={\begin{cases}\exp {\bigl (}{-\tau _{1}^{2}(x-\mu )^{2}/2}{\bigr )},&x<\mu ,\\[2mu]\exp {\bigl (}{-\tau _{2}^{2}(x-\mu )^{2}/2}{\bigr )},&x\geq \mu .\end{cases}}

То есть, g ( x ) напоминает кривую колокола с пиком при $x = μ$ , разбросом/стандартным отклонением слева от среднего значения и разбросом справа от среднего значения. При длине волны λ, измеренной в нанометрах , мы затем аппроксимируем 1931 функцию сопоставления цветов: $1/\tau _{1}$ $1/\tau _{2}$

{\begin{aligned}{\overline {x}}(\lambda )&=1.056\,g(\lambda ;599.8,0.0264,0.0323)+0.362\,g(\lambda ;442.0,0.0624,0.0374)\\[2mu]&\quad -0.065\,g(\lambda ;501.1,0.0490,0.0382),\\[5mu]{\overline {y}}(\lambda )&=0.821\,g(\lambda ;568.8,0.0213,0.0247)+0.286\,g(\lambda ;530.9,0.0613,0.0322),\\[5mu]{\overline {z}}(\lambda )&=1.217\,g(\lambda ;437.0,0.0845,0.0278)+0.681\,g(\lambda ;459.0,0.0385,0.0725).\end{aligned}}

Квадратичные разности между приведенным выше приближением и измеренными функциями сопоставления цветов CIE xyz меньше, чем дисперсия внутри наблюдателя, обнаруженная в экспериментальных измерениях, используемых для формирования стандартов CIE. Также возможно использовать меньше гауссовых функций, с одной гауссовой для каждой «доли». CIE 1964 хорошо соответствует однодолевой функции. ^[15]

Функции сопоставления цветов CIE XYZ неотрицательны и приводят к неотрицательным координатам XYZ для всех реальных цветов (то есть для неотрицательных спектров света). Другие наблюдатели, такие как для пространства CIE RGB или других цветовых пространств RGB , определяются другими наборами из трех функций сопоставления цветов, которые, как правило, не являются неотрицательными, и приводят к трехцветным значениям в этих других пространствах, которые могут включать отрицательные координаты для некоторых реальных цветов.

Вычисление XYZ по спектральным данным

Эмиссионный корпус

Трехцветные значения для цвета со спектральной яркостью L _e,Ω,λ задаются в терминах стандартного наблюдателя следующим образом:

{\begin{aligned}X&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {x}}(\lambda )\,d\lambda ,\\[6mu]Y&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,\\[6mu]Z&=\int _{\lambda }L_{\mathrm {e} ,\Omega ,\lambda }(\lambda )\,{\overline {z}}(\lambda )\,d\lambda .\end{aligned}}

где — длина волны эквивалентного монохроматического света (измеряется в нанометрах ), а обычные пределы интеграла равны . $\lambda$ $\lambda \in [380,780]$

Значения X , Y и Z ограничены, если ограничен спектр яркости L _{e,Ω,λ .}

Светоотражающие и пропускающие корпуса

Отражательный и пропускающий случаи очень похожи на излучательный случай, с несколькими отличиями. Спектральная яркость L _e,Ω,λ заменяется спектральным отражением (или пропусканием ) S(λ) измеряемого объекта, умноженным на спектральное распределение мощности источника света I(λ) .

{\begin{aligned}X&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {x}}(\lambda )\,d\lambda ,\\[8mu]Y&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,\\[8mu]Z&={\frac {K}{N}}\int _{\lambda }S(\lambda )\,I(\lambda )\,{\overline {z}}(\lambda )\,d\lambda ,\end{aligned}}

где

N=\int _{\lambda }I(\lambda )\,{\overline {y}}(\lambda )\,d\lambda ,

K — масштабный коэффициент (обычно 1 или 100) и длина волны эквивалентного монохроматического света (измеряется в нанометрах ), а стандартные пределы интеграла равны . $\lambda$ $\lambda \in [380,780]$

МКО ху.mw-parser-output .vanchor>:target~.vanchor-text{background-color:#b1d2ff}@media screen{html.skin-theme-clientpref-night .mw-parser-output .vanchor>:target~.vanchor-text{background-color:#0f4dc9}}@media screen and (prefers-color-scheme:dark){html.skin-theme-clientpref-os .mw-parser-output .vanchor>:target~.vanchor-text{background-color:#0f4dc9}}диаграмма цветностии цветовое пространство CIE xyY

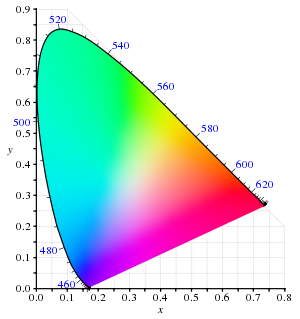
Поскольку человеческий глаз имеет три типа цветовых датчиков, которые реагируют на разные диапазоны длин волн , полный график всех видимых цветов представляет собой трехмерную фигуру. Однако концепцию цвета можно разделить на две части: яркость и цветность . Например, белый цвет является ярким цветом, в то время как серый цвет считается менее яркой версией того же белого. Другими словами, цветность белого и серого цветов одинакова, а их яркость различается.

Цветовое пространство CIE XYZ было намеренно разработано таким образом, чтобы параметр Y также был мерой яркости цвета. Затем цветность определяется двумя производными параметрами x и y , причем два из трех нормализованных значений являются функциями всех трех трехцветных значений X , Y и Z : ^[16]^{[ необходимо дополнительное объяснение ]}

{\begin{aligned}x&={\frac {X}{X+Y+Z}}\\[5mu]y&={\frac {Y}{X+Y+Z}}\\[5mu]z&={\frac {Z}{X+Y+Z}}=1-x-y\end{aligned}}

То есть, поскольку каждый трехцветный параметр X , Y , Z делится на сумму всех трех, то полученные значения x , y , z представляют собой долю целого, и поэтому их сумма должна быть равна единице. Таким образом, значение z можно вывести, зная x и y , и, следовательно, последних двух значений достаточно для описания цветности любого цвета.

Производное цветовое пространство, определяемое x , y и Y, известно как цветовое пространство CIE xyY и широко используется для указания цветов на практике.

Значения цветности X и Z можно рассчитать обратно из значений цветности x и y и значения цветности Y : ^[17]

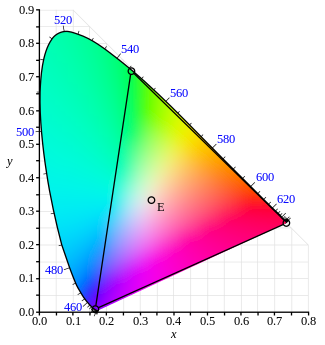
{\begin{aligned}X&={\frac {Y}{y}}x,\\[5mu]Z&={\frac {Y}{y}}(1-x-y).\end{aligned}}

На рисунке справа показана соответствующая диаграмма цветности. Внешняя изогнутая граница — это спектральное локус , где длины волн показаны в нанометрах. Диаграмма цветности — это инструмент для указания того, как человеческий глаз будет воспринимать свет с заданным спектром. Она не может определять цвета объектов (или печатных красок), поскольку цветность, наблюдаемая при взгляде на объект, зависит также от источника света.

Математически цвета диаграммы цветности занимают область действительной проективной плоскости .

Диаграмма цветности иллюстрирует ряд интересных свойств цветового пространства CIE XYZ:

Диаграмма представляет все цветности, видимые среднестатистическому человеку. Они показаны в цвете, и эта область называется гаммой человеческого зрения. Гамма всех видимых цветностей на графике CIE представляет собой фигуру в форме языка или подковы, показанную в цвете. Изогнутый край гаммы называется спектральным локусом и соответствует монохроматическому свету (каждая точка представляет собой чистый оттенок одной длины волны), с длинами волн, указанными в нанометрах. Прямой край в нижней части гаммы называется линией пурпурных цветов . Эти цвета, хотя они и находятся на границе гаммы, не имеют аналогов в монохроматическом свете. Менее насыщенные цвета появляются внутри фигуры с белым в центре.
Видно, что все видимые цветности соответствуют неотрицательным значениям x , y и z (и, следовательно, неотрицательным значениям X , Y и Z ).
Если выбрать любые две точки цвета на диаграмме цветности, то все цвета, которые лежат на прямой линии между двумя точками, могут быть образованы путем смешивания этих двух цветов. Из этого следует, что цветовая гамма должна иметь выпуклую форму. Все цвета, которые могут быть образованы путем смешивания трех источников, находятся внутри треугольника, образованного точками источника на диаграмме цветности (и так далее для нескольких источников).
Равная смесь двух одинаково ярких цветов, как правило, не будет лежать на середине этого отрезка линии . В более общих чертах, расстояние на диаграмме цветности CIE xy не соответствует степени различия между двумя цветами. В начале 1940-х годов Дэвид МакАдам изучал природу зрительной чувствительности к цветовым различиям и обобщил свои результаты в концепции эллипса МакАдама . На основе работы МакАдама были разработаны цветовые пространства CIE 1960 , CIE 1964 и CIE 1976 с целью достижения перцептивной однородности (имеют равное расстояние в цветовом пространстве, соответствующее равным различиям в цвете). Хотя они были явным улучшением по сравнению с системой CIE 1931, они не были полностью свободны от искажений.
Видно, что при наличии трех реальных источников эти источники не могут покрыть гамму человеческого зрения. Геометрически говоря, нет трех точек внутри гаммы, которые образуют треугольник, включающий всю гамму; или, проще говоря, гамма человеческого зрения не является треугольником.
Свет с плоским спектром мощности по длине волны (одинаковая мощность в каждом интервале 1 нм ) соответствует точке ( x , y ) = (1/3, 1/3) .

Смешивание цветов, указанных в диаграмме цветности CIE xy

При аддитивном смешивании двух или более цветов координаты цветности x и y результирующего цвета (x _mix ,y _mix ) могут быть рассчитаны из цветностей компонентов смеси (x ₁ ,y ₁ ; x ₂ ,y ₂ ; …; x _n ,y _n ) и соответствующих им яркостей (L ₁ , L ₂ , …, L _n ) по следующим формулам: ^[18]

x_{\mathrm {mix} }={\frac {{\dfrac {x_{1}}{y_{1}}}L_{1}+{\dfrac {x_{2}}{y_{2}}}L_{2}+\dots +{\dfrac {x_{n}}{y_{n}}}L_{n}}{{\dfrac {L_{1}}{y_{1}}}+{\dfrac {L_{2}}{y_{2}}}+\dots +{\dfrac {L_{n}}{y_{n}}}}}\quad ,\quad y_{\mathrm {mix} }={\frac {L_{1}+L_{2}+\dots +L_{n}}{{\dfrac {L_{1}}{y_{1}}}+{\dfrac {L_{2}}{y_{2}}}+\dots +{\dfrac {L_{n}}{y_{n}}}}}

Эти формулы могут быть получены из ранее представленных определений координат цветности x и y, используя тот факт, что трехцветные значения X, Y и Z отдельных компонентов смеси являются непосредственно аддитивными. Вместо значений яркости (L ₁ , L ₂ и т. д.) можно альтернативно использовать любую другую фотометрическую величину, которая прямо пропорциональна трехцветному значению Y (естественно, что само Y также может быть использовано).

Как уже упоминалось, при смешивании двух цветов результирующий цвет x _mix , y _mix будет лежать на отрезке прямой, соединяющей эти цвета на диаграмме цветности CIE xy. Для расчета соотношения смешивания компонентов цветов x ₁ ,y ₁ и x ₂ ,y ₂ , дающего определенный x _mix ,y _mix на этом отрезке, можно воспользоваться формулой

{\frac {L_{1}}{L_{2}}}={\frac {y_{1}\left(x_{2}-x_{\mathrm {mix} }\right)}{y_{2}\left(x_{\mathrm {mix} }-x_{1}\right)}}={\frac {y_{1}\left(y_{2}-y_{\mathrm {mix} }\right)}{y_{2}\left(y_{\mathrm {mix} }-y_{1}\right)}}

где L ₁ — яркость цвета x ₁ ,y ₁ , а L ₂ — яркость цвета x ₂ ,y ₂ . Поскольку y _mix однозначно определяется x _mix и наоборот, для расчета соотношения смешивания достаточно знать только одно из них. В соответствии с замечаниями относительно формул для x _mix и y _mix , соотношение смешивания L ₁ /L ₂ вполне может быть выражено через другие фотометрические величины, нежели яркость.

Определение цветового пространства CIE XYZ

Цветовое пространство CIE RGB

Первым шагом в разработке цветового пространства CIE XYZ является измерение цветового пространства CIE RGB. Цветовое пространство CIE RGB является одним из многих цветовых пространств RGB , отличающихся определенным набором монохроматических (одноволновых) основных цветов .

В 1920-х годах два независимых эксперимента по восприятию цвета человеком были проведены У. Дэвидом Райтом ^[3] с десятью наблюдателями и Джоном Гилдом ^[4] с семью наблюдателями. Их результаты заложили основу для спецификации трихроматического цветового пространства CIE XYZ.

Эксперименты проводились с использованием круглого разделенного экрана (двухчастного поля) диаметром 2 градуса, что соответствует угловому размеру человеческой ямки. С одной стороны проецировался тестовый цвет, а с другой — цвет, настраиваемый наблюдателем. Настраиваемый цвет представлял собой смесь трех монохроматических основных цветов, каждый с настраиваемой яркостью. Наблюдатель изменял яркость каждого из трех основных лучей до тех пор, пока не наблюдалось совпадение с тестовым цветом.

Если бы тестовый цвет был просто монохроматическим цветом на длине волны λ, и если бы он мог быть сопоставлен с комбинацией трех основных цветов с относительной интенсивностью , и соответственно, то табулирование этих значений при различных λ оценит три функции длины волны. Это функции сопоставления цветов RGB. Любое спектральное распределение можно рассматривать как комбинацию ряда монохроматических источников с различной интенсивностью, так что (по законам Грассмана ) интегрирование функций сопоставления цветов с этим спектральным распределением даст интенсивности трех основных цветов, необходимые для сопоставления. Проблема в том, что три основных цвета могут производить только цвета, которые лежат в пределах их гаммы - треугольника в цветовом пространстве, образованного основными цветами, который никогда не касается монохроматического локуса или фиолетовой линии , за исключением трех основных цветов. Другими словами, нет монохроматического источника, который мог бы быть сопоставлен с комбинацией трех основных цветов, за исключением длин волн самих трех основных цветов. Однако, добавляя один из основных цветов к монохроматическому тестовому цвету, тестовый цвет можно ввести в гамму RGB, что позволит выполнить сопоставление. Добавление основного цвета к монохроматическому тестовому цвету фактически то же самое, что и вычитание его из регулируемого цвета, что, конечно, невозможно сделать, поскольку невозможно иметь отрицательную интенсивность для любого из основных цветов. ${\bar {r}}(\lambda )$ ${\bar {g}}(\lambda )$ ${\bar {b}}(\lambda )$

Для длин волн между синим и зеленым основными цветами необходимо добавить немного красного основного цвета, чтобы обеспечить сопоставление, что приводит к отрицательным значениям . Аналогично, между зеленым и красным основными цветами необходимо добавить немного синего цвета, и это будет отрицательно. Для длин волн ниже длины волны синего основного цвета или выше длины волны красного основного цвета необходимо добавить немного зеленого цвета, и это будет отрицательно. В каждом случае оставшиеся две функции сопоставления цветов будут положительными. Можно видеть, что отклонение гаммы RGB от полной гаммы довольно мало, за исключением области между синим и зеленым основными цветами при 435,8 и 546,1 нм. В этом диапазоне длин волн необходимо добавить довольно большое количество красного основного цвета к тестовому цвету, и именно в этом диапазоне функция сопоставления красного цвета имеет довольно большие отрицательные значения. В своих областях отрицательных значений функции сопоставления зеленого и синего цветов имеют довольно маленькие отрицательные значения. ${\bar {r}}(\lambda )$ ${\bar {b}}(\lambda )$ ${\bar {g}}(\lambda )$

Хотя эксперименты Райта и Гилда проводились с использованием различных основных цветов различной интенсивности и хотя они использовали ряд различных наблюдателей, все их результаты были обобщены стандартизированными функциями сопоставления цветов CIE RGB , , и , полученными с использованием трех монохроматических основных цветов на стандартизированных длинах волн 700 нм (красный), 546,1 нм (зеленый) и 435,8 нм (синий). (Ненормализованные) функции сопоставления цветов представляют собой количество основных цветов, необходимое для сопоставления монохроматического тестового основного цвета. Эти функции показаны на графике справа (CIE 1931). и равны нулю при 435,8 нм , и равны нулю при 546,1 нм и и равны нулю при 700 нм , поскольку в этих случаях тестовый цвет является одним из основных цветов. Основные цвета с длинами волн 546,1 нм и 435,8 нм были выбраны потому, что они являются легко воспроизводимыми монохроматическими линиями разряда паров ртути. Длина волны 700 нм , которую в 1931 году было трудно воспроизвести в виде монохроматического луча, была выбрана потому, что восприятие цвета глазом при этой длине волны довольно неизменно, и поэтому небольшие ошибки в длине волны этого основного луча не оказали бы существенного влияния на результаты. ${\overline {r}}(\lambda )$ ${\overline {g}}(\lambda )$ ${\overline {b}}(\lambda )$ ${\overline {r}}(\lambda )$ ${\overline {g}}(\lambda )$ ${\overline {r}}(\lambda )$ ${\overline {b}}(\lambda )$ ${\overline {g}}(\lambda )$ ${\overline {b}}(\lambda )$

Функции цветового соответствия и основные цвета были установлены специальной комиссией CIE после значительных обсуждений. ^[19] Отсечки на коротковолновой и длинноволновой стороне диаграммы выбраны несколько произвольно; человеческий глаз на самом деле может видеть свет с длиной волны до примерно 810 нм , но с чувствительностью, которая во много тысяч раз ниже, чем для зеленого света. Эти функции цветового соответствия определяют то, что известно как «стандартный наблюдатель CIE 1931 года». Вместо того, чтобы указывать яркость каждого основного цвета, кривые нормализуются так, чтобы иметь постоянную площадь под ними. Эта площадь фиксируется на определенном значении, указывая, что

\int _{0}^{\infty }{\overline {r}}(\lambda )\,d\lambda =\int _{0}^{\infty }{\overline {g}}(\lambda )\,d\lambda =\int _{0}^{\infty }{\overline {b}}(\lambda )\,d\lambda .

Полученные нормализованные функции сопоставления цветов затем масштабируются в соотношении r:g:b 1:4,5907:0,0601 для яркости источника и 72,0962:1,3791:1 для сияния источника для воспроизведения истинных функций сопоставления цветов. Предложив стандартизировать основные цвета, CIE создала международную систему объективной цветовой нотации.

При наличии этих масштабированных функций сопоставления цветов трехцветные значения RGB для цвета со спектральным распределением мощности будут определяться следующим образом: $S(\lambda )$

{\begin{aligned}R&=\int _{0}^{\infty }S(\lambda )\,{\overline {r}}(\lambda )\,d\lambda ,\\[6mu]G&=\int _{0}^{\infty }S(\lambda )\,{\overline {g}}(\lambda )\,d\lambda ,\\[6mu]B&=\int _{0}^{\infty }S(\lambda )\,{\overline {b}}(\lambda )\,d\lambda .\end{aligned}}

Все это внутренние продукты , и их можно рассматривать как проекцию бесконечномерного спектра на трехмерный цвет .

Законы Грассмана

Можно задать вопрос: «Почему результаты Райта и Гилда можно обобщить, используя другие основные цвета и другие интенсивности, нежели те, которые используются на самом деле?» Можно также задать вопрос: «А как быть в случае, когда сопоставляемые тестовые цвета не являются монохроматическими?» Ответ на оба этих вопроса заключается в (почти) линейности человеческого восприятия цвета. Эта линейность выражена в законах цвета Грассмана.

Пространство CIE RGB можно использовать для определения цветности обычным способом: координаты цветности — r , g и b , где:

{\begin{aligned}r&={\frac {R}{R+G+B}},\\[5mu]g&={\frac {G}{R+G+B}},\\[5mu]b&={\frac {B}{R+G+B}}.\end{aligned}}

Построение цветового пространства CIE XYZ на основе данных Райта–Гилда

Цветовой охват sRGB ( слева ) и видимый цветовой охват при освещении D65 ( справа ), спроецированные в цветовом пространстве CIEXYZ. X и Z — горизонтальные оси; Y — вертикальная ось.

Цветовой охват sRGB ( слева ) и видимый цветовой охват при освещении D65 ( справа ), спроецированные в цветовом пространстве CIExyY. x и y — горизонтальные оси; Y — вертикальная ось.

Разработав модель RGB человеческого зрения с использованием функций сопоставления CIE RGB, члены специальной комиссии захотели разработать другое цветовое пространство, которое будет связано с цветовым пространством CIE RGB. Предполагалось, что закон Грассмана будет выполнен, и новое пространство будет связано с пространством CIE RGB линейным преобразованием. Новое пространство будет определено в терминах трех новых функций сопоставления цветов , , и как описано выше. Новое цветовое пространство будет выбрано таким образом, чтобы оно имело следующие желаемые свойства: ${\overline {x}}(\lambda )$ ${\overline {y}}(\lambda )$ ${\overline {z}}(\lambda )$

Новые функции сопоставления цветов должны были быть везде больше или равны нулю. В 1931 году вычисления выполнялись вручную или с помощью логарифмической линейки, а спецификация положительных значений была полезным вычислительным упрощением.
Функция сопоставления цветов будет точно равна функции фотопической световой эффективности V ( λ ) для «стандартного фотопического наблюдателя CIE». ^[20] Функция яркости описывает изменение воспринимаемой яркости в зависимости от длины волны. Тот факт, что функция яркости может быть построена с помощью линейной комбинации функций сопоставления цветов RGB, не гарантировался никакими средствами, но можно было ожидать, что это будет почти верно из-за почти линейной природы человеческого зрения. Опять же, основной причиной этого требования было вычислительное упрощение. ${\overline {y}}(\lambda )$
Для постоянной энергии белой точки требовалось, чтобы x = y = z = 1/3 .
В силу определения цветности и требования положительных значений x и y видно, что гамма всех цветов будет лежать внутри треугольника [1, 0], [0, 0], [0, 1]. Требовалось, чтобы гамма заполняла это пространство практически полностью.
Было обнаружено, что функция сопоставления цветов может быть установлена на ноль выше 650 нм , оставаясь в пределах экспериментальной погрешности. Для простоты вычислений было указано, что это так. ${\overline {z}}(\lambda )$

В геометрических терминах выбор нового цветового пространства равносилен выбору нового треугольника в пространстве цветности rg . На рисунке справа вверху координаты цветности rg показаны на двух осях черным цветом вместе с гаммой стандартного наблюдателя 1931 года. Красным цветом показаны оси цветности CIE xy , которые были определены вышеуказанными требованиями. Требование, чтобы координаты XYZ были неотрицательными, означает, что треугольник, образованный C _r , C _g , C _{b ,} должен охватывать всю гамму стандартного наблюдателя. Линия, соединяющая C _r и C _{b ,} фиксируется требованием, чтобы функция была равна функции яркости. Эта линия является линией нулевой яркости и называется алихной. Требование, чтобы функция была равна нулю выше 650 нм, означает, что линия, соединяющая C _g и C _{r ,} должна быть касательной к гамме в области K _r . Это определяет местоположение точки C _r . Требование, чтобы точка равной энергии определялась как x = y = 1/3, накладывает ограничение на линию, соединяющую C _b и C _g , и, наконец, требование, чтобы гамма заполняла пространство, накладывает второе ограничение на эту линию, чтобы она была очень близка к гамме в зеленой области, которая определяет местоположение C _g и C _b . Описанное выше преобразование является линейным преобразованием из пространства CIE RGB в пространство XYZ. Стандартизированное преобразование, принятое специальной комиссией CIE, было следующим: ${\overline {y}}(\lambda )$ ${\overline {z}}(\lambda )$

Числа в матрице преобразования ниже являются точными, с количеством цифр, указанным в стандартах CIE. ^[19]

{\begin{aligned}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}&={\begin{bmatrix}b_{11}&b_{12}&b_{13}\\b_{21}&b_{22}&b_{23}\\b_{31}&b_{32}&b_{33}\end{bmatrix}}{\begin{bmatrix}R\\G\\B\end{bmatrix}}\\[10mu]&={\begin{bmatrix}0.490\,00&0.310\,00&0.200\,00\\0.176\,97&0.812\,40&0.010\,63\\0.000\,00&0.010\,00&0.990\,00\end{bmatrix}}{\begin{bmatrix}R\\G\\B\end{bmatrix}}\end{aligned}}

Приведенная выше матрица сбалансирована для равноэнергетического стимула: она имеет координаты (1,1,1) как в координатах RGB, так и в координатах XYZ.

В то время как указанная выше матрица точно указана в стандартах, обратная матрица остается неопределенной, чтобы ее можно было аппроксимировать с точностью машины для уменьшения ошибок округления. Ее значения можно точно вычислить с использованием рациональных чисел:

{\begin{bmatrix}R\\G\\B\end{bmatrix}}={\frac {1}{3400850}}{\begin{bmatrix}8041697&-3049000&-1591847\\-1752003&4851000&301853\\17697&-49000&3432153\end{bmatrix}}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}

Который имеет следующие приблизительные значения:

{\begin{bmatrix}R\\G\\B\end{bmatrix}}\approx {\begin{bmatrix}2.364\,61385&-0.896\,54057&-0.468\,07328\\-0.515\,16621&1.426\,4081&0.088\,7581\\0.005\,2037&-0.014\,40816&1.009\,20446\end{bmatrix}}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}

Основные цвета XYZ будут иметь координаты XYZ [1,0,0], [0,1,0] и [0,0,1] в пространстве XYZ, поэтому столбцы обратной матрицы выше определяют основные цвета XYZ (Cr, Cg и Cb) в пространстве RGB. Разделив каждый столбец на его сумму, получим координаты основных цветов XYZ в пространстве RGB, что дает:

Кр = {1,27496, -0,27777, 0,00280576}

Сг = {-1,7393, 2,76726, -0,0279521}

Сб = {-0,743104, 0,140911, 1,60219}

Координаты r и g основных цветов XYZ указаны на диаграмме пространства цветности rg выше.

Интегралы функций цветового соответствия XYZ должны быть равны согласно требованию 3 выше, и это устанавливается интегралом функции фотопической световой эффективности согласно требованию 2 выше. Табличные кривые чувствительности имеют определенную долю произвольности. Формы отдельных кривых чувствительности X , Y и Z могут быть измерены с разумной точностью. Однако общая кривая светимости (которая на самом деле является взвешенной суммой этих трех кривых) субъективна, поскольку она включает в себя вопрос к испытуемому, имеют ли два источника света одинаковую яркость, даже если они совершенно разных цветов. В том же духе относительные величины кривых X , Y и Z произвольны. Более того, можно определить действительное цветовое пространство с помощью кривой чувствительности X , которая имеет вдвое большую амплитуду. Это новое цветовое пространство будет иметь другую форму. Кривые чувствительности в цветовых пространствах CIE 1931 и 1964 XYZ масштабируются так, чтобы иметь равные площади под кривыми.

Последующие уточнения

Доступно несколько других функций сопоставления цветов в стиле XYZ, исправляющих известные проблемы в исходном цветовом пространстве 1931 года. Эти функции подразумевают собственные цветовые пространства в стиле XYZ и xyY. ^[21]

Поправки Джадда и Воса для 2° CMF: Самой серьезной проблемой функций сопоставления цветов CIE XYZ 1931 года является ошибка в фотопическом Y (или функции на синем конце спектра). ^[22] Исправления Джадда (1951) и его последующих исправлений Воса (1978) ^[23] были направлены на исправление этой проблемы без отклонения от первоначальной методологии. ^[21] $V(\lambda )$
МКО 1964 X ₁₀ Y ₁₀ Z ₁₀: X ₁₀ Y ₁₀ Z ₁₀ (также пишется как XYZ ₁₀ и аналогично для следующего) — это цветовое пространство в стиле XYZ, определенное с использованием CIE 1964 10° наблюдателя CMF. ^[24] 3 CMF в основном получены из функций сопоставления цветов RGB Стайлза и Берча, ^[25] которые в отличие от функций Райта–Гилда (и последующих поправок Джадда–Воса) «непосредственно измеряются», что освобождает их от ошибок реконструкции функций 1931 года. ^[21]; Стайлз и Берч также опубликовали набор 2° функций сопоставления цветов RGB; однако ни одно пространство XYZ, полученное из них, не было официально признано CIE. ^[21]
МКО 170-2 X _F Y _F Z _F: X _F Y _F Z _F — это цветовое пространство в стиле XYZ, определенное с использованием физиологического наблюдателя Stockman & Sharpe (2000) 2°, который, в свою очередь, является линейной комбинацией функций отклика колбочек LMS . ^[26] Данные CMF, наряду с набором физиологических данных 10°, доступны в лаборатории исследований цвета и зрения Университетского колледжа Лондона с разрешением до 0,1 нм. ^[27]
CIE 170-2 X _F,10 Y _F,10 Z _F,10: Это пространство основано на физиологическом 10-градусном наблюдателе Стокмана и Шарпа (2000). ^[26]

По данным Konica Minolta , более старая модель CIE 1931 CMF демонстрирует ошибку метамеризма (неспособность предсказать, когда цвета будут выглядеть одинаково) для дисплеев с широким цветовым охватом , содержащих узкополосные излучатели, такие как OLED , тогда как модель XYZ _F CMF 2015 года не подвержена этому. ^[28] В более старых руководствах Sony рекомендуется использовать коррекцию Джадда-Воса, применяя смещение к белой точке в зависимости от используемой технологии отображения.

Смотрите также

Трихроматия
Невозможный цвет
Цветовое пространство CIELAB
Стандартный источник света , определение белой точки, используемое CIE и обычно отображаемое на диаграммах цветового пространства как E, D50 или D65.

Ссылки

^ CIE (1932). Протоколы Международной комиссии по освещению, 1931 год . Кембридж: Издательство Кембриджского университета .
^ Смит, Томас; Гилд, Джон (1931–32). «Колориметрические стандарты CIE и их использование». Труды Оптического общества . 33 (3): 73–134. Bibcode : 1931TrOS...33...73S. doi : 10.1088/1475-4878/33/3/301.
^ ab Райт, Уильям Дэвид (1928). «Переопределение трихроматических коэффициентов спектральных цветов». Труды Оптического общества . 30 (4): 141–164. doi :10.1088/1475-4878/30/4/301.
^ ab Guild, J. (1932). "Колориметрические свойства спектра". Philosophical Transactions of the Royal Society of London. Серия A, содержащая статьи математического или физического характера . 230 (681–693): 149–187. Bibcode : 1932RSPTA.230..149G. doi : 10.1098/rsta.1932.0005 . JSTOR 91229. Трихроматические коэффициенты для десяти наблюдателей [Райта] так близко совпадали с коэффициентами семи наблюдателей, обследованных в Национальной физической лаборатории, что это указывает на то, что обе группы должны давать результаты, приближающиеся к "нормальным" более близко, чем можно было бы ожидать, исходя из размера любой из групп
^ "- YouTube". YouTube . Архивировано из оригинала 2016-03-17 . Получено 2015-10-17 .Трехцветное значение цвета: независимое от устройства представление цвета
^ Хант, Р. В. (1998). Измерение цвета (3-е изд.). Англия: Fountain Press. ISBN 0-86343-387-1.. См. стр. 39–46 для получения информации об основах трехкомпонентных цветовых моделей в физиологии человеческого глаза и 54–7 для координат цветности.
^ «Рагнар Гранит — Сенсорная структура сетчатки и зрения». www.japi.org .
^ Шанда, Янош, изд. (27 июля 2007 г.). Колориметрия . п. 305. дои : 10.1002/9780470175637. ISBN 9780470175637.
^ Stiles, WS; Birch, JM (1959). "Исследование соответствия цветов NPL: Заключительный отчет (1958)". Optica Acta . 6 (1): 1–26. Bibcode : 1959AcOpt...6....1S. doi : 10.1080/713826267.
^ Сперанская, Н.И. (1959). «Определение координат цвета спектра для двадцати семи нормальных наблюдателей». Оптика и спектроскопия . 7 : 424–428.
^ "CIE Free Documents for Download". Архивировано из оригинала 2017-08-28 . Получено 2017-08-28 .
^ Глинн, Эрл Ф. «Отчет по лабораторной работе по диаграммам цветности».
^ "CIE 15: Технический отчет: Колориметрия, 3-е издание". Окончательные данные, относящиеся к стандартным колориметрическим источникам света и наблюдателям, даны с интервалом в 1 нм в соответствующих стандартах CIE [CIE, 1998c (будет заменено на CIE, 2004a); CIE, 1986a].
^ Harris, AC; Weatherall, IL (сентябрь 1990 г.). «Объективная оценка вариации цвета у жука-песочника Chaerodes trachyscelides White (Coleoptera: Tenebrionidae) с помощью инструментального определения значений CIE LAB». Журнал Королевского общества Новой Зеландии . 20 (3). Королевское общество Новой Зеландии: 253–259. Bibcode : 1990JRSNZ..20..253H. doi : 10.1080/03036758.1990.10416819 . Архивировано из оригинала 08.03.2017.
^ ab Wyman, Chris; Sloan, Peter-Pike; Shirley, Peter (12 июля 2013 г.). «Простые аналитические аппроксимации функций сопоставления цветов CIE XYZ». Журнал компьютерных графических технологий . 2 (2): 1-11. ISSN 2331-7418.
^ Пойнтон, Чарльз (2012). Цифровое видео и HD - Алгоритмы и интерфейсы (2-е изд.). С. 275. Уравнение 25.1
^ Пойнтон, Чарльз (2012). Цифровое видео и HD - Алгоритмы и интерфейсы (2-е изд.). С. 275. Уравнение 25.2
^ «Изучите науку о цвете, чтобы добиться максимального успеха при использовании светодиодов – часть 2 – Журнал LEDs, выпуск 7/2012». 18 июля 2012 г. Архивировано из оригинала 11.11.2017.
^ ab Fairman, HS; Brill, MH; Hemmendinger, H. (февраль 1997 г.). «Как функции сопоставления цветов CIE 1931 г. были получены из данных Райта–Гилда». Color Research and Application . 22 (1): 11–23. doi :10.1002/(SICI)1520-6378(199702)22:1<11::AID-COL4>3.0.CO;2-7. и Фэрман, Х.С.; Брилл, М.Х.; Хеммендингер, Х. (август 1998 г.). «Исправление: как функции сопоставления цветов CIE 1931 г. были получены из данных Райта–Гильда». Color Research and Application . 23 (4): 259. doi : 10.1002/(SICI)1520-6378(199808)23:4<259::AID-COL18>3.0.CO;2-7 .
^ CIE (1926). Дела Международной комиссии по освещению, 1924 год . Кембридж: Издательство Кембриджского университета .Функция световой эффективности 1924 года серьезно занижала чувствительность на длинах волн ниже 460 нм и была дополнена более новыми и точными кривыми светимости; см. Функция светимости#Усовершенствования стандарта .
^ abcd "CMF introduction". Лаборатория исследований цвета и зрения . Институт офтальмологии, Университетский колледж Лондона. Архивировано из оригинала 19 ноября 2023 г.
^ Стокман, Эндрю (декабрь 2019 г.). «Основы конуса и стандарты CIE» (PDF) . Current Opinion in Behavioral Sciences . 30 : 87–93. doi :10.1016/j.cobeha.2019.06.005 . Получено 27 октября 2023 г. .
^ Вос, Дж. Дж. (сентябрь 1978 г.). «Колориметрические и фотометрические свойства 2° фундаментального наблюдателя». Color Research & Application . 3 (3): 104–156. doi :10.1002/col.5080030309.
^ "XYZ Tristimulus Value (CIE 1931) / Tristimulus Value (CIE 1964) - Часть IV - Точная цветовая связь". KONICA MINOLTA . Архивировано из оригинала 19 ноября 2023 г.
^ Stiles, WS; Burch, JM (1959). "Исследование соответствия цветов NPL: окончательный отчет". Optica Acta . 6 (1). Bibcode : 1959AcOpt...6....1S. doi : 10.1080/713826267.
^ ab CIE 170-2:2015: Основная диаграмма цветности с физиологическими осями – Часть 2: Функции спектральной световой эффективности и диаграммы цветности. CIE. ISBN 978-3-902842-05-3. Архивировано из оригинала 19 ноября 2023 г.
^ "CIE functions". Исследовательская лаборатория цвета и зрения . Институт офтальмологии, Университетский колледж Лондона. Архивировано из оригинала 19 ноября 2023 г.
^ "Устранение проблемы соответствия цветов дисплея" (PDF) . KONICA MINOLTA .

Дальнейшее чтение

Broadbent, Arthur D. (август 2004 г.). «Критический обзор разработки функций цветового соответствия CIE1931 RGB». Color Research & Application . 29 (4): 267–272. doi :10.1002/col.20020. В этой статье описывается разработка координат цветности CIE1931 и функций цветового соответствия, начиная с исходных экспериментальных данных WD Wright и J. Guild. Приведено достаточно информации, чтобы позволить читателю воспроизвести и проверить результаты, полученные на каждом этапе вычислений, и критически проанализировать используемые процедуры. К сожалению, часть информации, необходимой для преобразования координат, так и не была опубликована, а в прилагаемых таблицах приведены вероятные версии этих недостающих данных.
Trezona, Pat W. (2001). «Вывод функций сопоставления цветов CIE 10° XYZ 1964 года и их применимость в фотометрии». Color Research and Application . 26 (1): 67–75. doi :10.1002/1520-6378(200102)26:1<67::AID-COL7>3.0.CO;2-4.
Райт, Уильям Дэвид (2007). «Золотой юбилей цвета в CIE — исторический и экспериментальный фон для системы колориметрии CIE 1931 года». В Schanda, János (ред.). Колориметрия . Wiley Interscience. стр. 9–24. doi :10.1002/9780470175637.ch2. ISBN 978-0-470-04904-4.(первоначально опубликовано Обществом красильщиков и колористов , Брэдфорд, 1981 г.)

Внешние ссылки

Введение в науку о цвете, Уильям Эндрю Стир.
Отчет по лабораторной работе «Цветовые диаграммы хроматичности» компании efg и исходный код Delphi
Цветовое пространство CIE, Гернот Хоффманн
Аннотированные загружаемые таблицы данных, Эндрю Стокман и Линдси Т. Шарп.
Расчет на основе исходных экспериментальных данных стандартного наблюдателя CIE 1931 RGB спектральных координат цветности и функций цветового соответствия
Colorlab MATLAB toolbox для вычисления цвета и точного воспроизведения цвета (от Jesus Malo и Maria Jose Luque, Universitat de Valencia). Он включает в себя стандартную трехцветную колориметрию CIE и преобразования в ряд нелинейных моделей цветового восприятия (CIE Lab, CIE CAM и т. д.).
Точная цветовая коммуникация. Взгляд на прошлое и будущее светодиодного биннинга.
[1] Измерение цвета в мире света