An existential graph is a type of diagrammatic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote on graphical logic as early as 1882,[1] and continued to develop the method until his death in 1914. They include both a separate graphical notation for logical statements and a logical calculus, i.e. (essentially) a formal system of rules of inference that can be used to derive new theorems from existing ones.
Peirce founded the algebraic notation (i.e. symbolic notation) of logic, especially that of predicate logic[2], which was still very new during his lifetime and which he himself played a major role in developing, to be philosophically unsatisfactory, because the symbols had their meaning by mere convention. In contrast, he strove for a style of writing in which the signs literally carry their meaning within them[3] – in the terminology of his theory of signs: a system of iconic signs that resemble or resemble the represented objects and relations. [4]
Thus, the development of an iconic, graphic and – as he intended – intuitive and easy-to-learn logical system was a project that Peirce worked on throughout his life. After at least one aborted approach – the "Entitative Graphs" – the closed system of Existential Graphs finally emerged from 1896 onwards. Although considered by their creator to be a clearly superior and more intuitive system, as a mode of writing and as a calculus, they had no major influence on the history of logic; On the one hand, this is attributed to the fact that Peirce published little on this topic and that the published texts were not written in a very understandable way;[5] and on the other hand, that the linear formula notation in the hands of experts is the less complex tool to handle[6]. For example, the existential graphs received little attention[7] or were seen as an unwieldy way of writing[8]. From 1963 onwards, works by Don D. Roberts and J. Jay Zeman, in which Peirce's graphic systems were systematically examined and presented, led to a better understanding. Today, however, only one modern application plays a practical role, the conceptual graphs introduced by John F. Sowa in 1976, which are used in computer science to represent knowledge. Existential graphs are increasingly reappearing as a subject of research in connection with a growing interest in graphical logic,[8] which is also expressed in attempts to replace the rules of inference given by Peirce with more intuitive ones. [9]
The overall system of existential graphs is composed of three subsystems that build on each other, the alpha graphs, the beta graphs and the gamma graphs. The alpha graphs are a purely propositional logical system. Building on this, the beta graphs are a first order logical calculus. The gamma graphs, which have not yet been fully researched and were not completed by Peirce, are understood as a further development of the alpha and beta graphs. When interpreted appropriately, the gamma graphs cover higher-level predicate logic as well as modal logic. As late as 1903, Peirce began a new approach, the "Tinctured Existential Graphs," with which he wanted to replace the previous systems of alpha, beta and gamma graphs and combine their expressiveness and performance in a single new system. Like the gamma graphs, the "Tinctured Existential Graphs" remained unfinished.
As calculi, the alpha, beta and gamma graphs are sound (i.e., all expressions derived as graphs are semantically valid). The alpha and beta graphs are also complete (i.e., all propositional or predicate-logically semantically valid expressions can be derived as alpha or beta graphs). [10]
Peirce proposed three systems of existential graphs:
Alpha nests in beta and gamma. Beta does not nest in gamma, quantified modal logic being more general than put forth by Peirce.
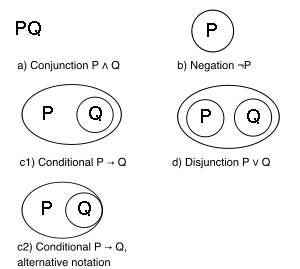
The syntax is:
Any well-formed part of a graph is a subgraph.
The semantics are:
Hence the alpha graphs are a minimalist notation for sentential logic, grounded in the expressive adequacy of And and Not. The alpha graphs constitute a radical simplification of the two-element Boolean algebra and the truth functors.
The depth of an object is the number of cuts that enclose it.
Rules of inference:
Rules of equivalence:
A proof manipulates a graph by a series of steps, with each step justified by one of the above rules. If a graph can be reduced by steps to the blank page or an empty cut, it is what is now called a tautology (or the complement thereof, a contradiction). Graphs that cannot be simplified beyond a certain point are analogues of the satisfiable formulas of first-order logic.

Peirce notated predicates using intuitive English phrases; the standard notation of contemporary logic, capital Latin letters, may also be employed. A dot asserts the existence of some individual in the domain of discourse. Multiple instances of the same object are linked by a line, called the "line of identity". There are no literal variables or quantifiers in the sense of first-order logic. A line of identity connecting two or more predicates can be read as asserting that the predicates share a common variable. The presence of lines of identity requires modifying the alpha rules of Equivalence.
The beta graphs can be read as a system in which all formula are to be taken as closed, because all variables are implicitly quantified. If the "shallowest" part of a line of identity has even (odd) depth, the associated variable is tacitly existentially (universally) quantified.
Zeman (1964) was the first to note that the beta graphs are isomorphic to first-order logic with equality (also see Zeman 1967). However, the secondary literature, especially Roberts (1973) and Shin (2002), does not agree on how this is. Peirce's writings do not address this question, because first-order logic was first clearly articulated only some years after his death, in the 1928 first edition of David Hilbert and Wilhelm Ackermann's Principles of Mathematical Logic.
Add to the syntax of alpha a second kind of simple closed curve, written using a dashed rather than a solid line. Peirce proposed rules for this second style of cut, which can be read as the primitive unary operator of modal logic.
Zeman (1964) was the first to note that straightforward emendations of the gamma graph rules yield the well-known modal logics S4 and S5. Hence the gamma graphs can be read as a peculiar form of normal modal logic. This finding of Zeman's has gone unremarked to this day, but is nonetheless included here as a point of interest.
The existential graphs are a curious offspring of Peirce the logician/mathematician with Peirce the founder of a major strand of semiotics. Peirce's graphical logic is but one of his many accomplishments in logic and mathematics. In a series of papers beginning in 1867, and culminating with his classic paper in the 1885 American Journal of Mathematics, Peirce developed much of the two-element Boolean algebra, propositional calculus, quantification and the predicate calculus, and some rudimentary set theory. Model theorists consider Peirce the first of their kind. He also extended De Morgan's relation algebra. He stopped short of metalogic (which eluded even Principia Mathematica).
But Peirce's evolving semiotic theory led him to doubt the value of logic formulated using conventional linear notation, and to prefer that logic and mathematics be notated in two (or even three) dimensions. His work went beyond Euler's diagrams and Venn's 1880 revision thereof. Frege's 1879 Begriffsschrift also employed a two-dimensional notation for logic, but one very different from Peirce's.
Peirce's first published paper on graphical logic (reprinted in Vol. 3 of his Collected Papers) proposed a system dual (in effect) to the alpha existential graphs, called the entitative graphs. He very soon abandoned this formalism in favor of the existential graphs. In 1911 Victoria, Lady Welby showed the existential graphs to C. K. Ogden who felt they could usefully be combined with Welby's thoughts in a "less abstruse form."[9] Otherwise they attracted little attention during his life and were invariably denigrated or ignored after his death, until the PhD theses by Roberts (1964) and Zeman (1964).
Currently, the chronological critical edition of Peirce's works, the Writings, extends only to 1892. Much of Peirce's work on logical graphs consists of manuscripts written after that date and still unpublished. Hence our understanding of Peirce's graphical logic is likely to change as the remaining 23 volumes of the chronological edition appear.