ША-2

Набор криптографических хеш-функций, разработанных АНБ

SHA-2 ( Secure Hash Algorithm 2 ) — это набор криптографических хеш-функций, разработанных Агентством национальной безопасности США (АНБ) и впервые опубликованных в 2001 году. ^{[3] [4]} Они построены с использованием конструкции Меркла–Дамгарда , из односторонней функции сжатия, построенной с использованием структуры Дэвиса–Майера из специализированного блочного шифра.

SHA-2 включает в себя значительные изменения по сравнению со своим предшественником SHA-1 . Семейство SHA-2 состоит из шести хэш-функций с дайджестами (хэш-значениями), которые составляют 224, 256, 384 или 512 бит: ^[5] SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, SHA-512/256 . SHA-256 и SHA-512 — это новые хэш-функции, дайджесты которых составляют восемь 32-битных и 64-битных слов соответственно. Они используют разные величины сдвига и аддитивные константы, но в остальном их структуры практически идентичны, отличаясь только количеством раундов. SHA-224 и SHA-384 — это усеченные версии SHA-256 и SHA-512 соответственно, вычисленные с разными начальными значениями. SHA-512/224 и SHA-512/256 также являются усеченными версиями SHA-512, но начальные значения генерируются с использованием метода, описанного в Федеральных стандартах обработки информации (FIPS) PUB 180-4.

SHA-2 был впервые опубликован Национальным институтом стандартов и технологий (NIST) в качестве федерального стандарта США. Семейство алгоритмов SHA-2 запатентовано в США ^[6] Соединенные Штаты выпустили патент по бесплатной лицензии. ^[5]

По состоянию на 2011 год ^{[обновлять]}лучшие публичные атаки преодолевают сопротивление прообраза для 52 из 64 раундов SHA-256 или 57 из 80 раундов SHA-512, а также сопротивление коллизии для 46 из 64 раундов SHA-256. ^{[1] [2]}

Стандарт хэширования

Одна итерация в функции сжатия семейства SHA-2. Синие компоненты выполняют следующие операции: Побитовое вращение использует различные константы для SHA-512. Указанные числа относятся к SHA-256. Красный — это сложение по модулю 2 ³² для SHA-256 или 2 ⁶⁴ для SHA-512.
     ${\displaystyle \operatorname {Ch} (E,F,G)=(E\land F)\oplus (\neg E\land G)}$
     ${\displaystyle \operatorname {Ma} (A,B,C)=(A\land B)\oplus (A\land C)\oplus (B\land C)}$
     ${\displaystyle \Sigma _{0}(A)=(A\!\ggg \!2)\oplus (A\!\ggg \!13)\oplus (A\!\ggg \!22)}$
     ${\displaystyle \Sigma _{1}(E)=(E\!\ggg \!6)\oplus (E\!\ggg \!11)\oplus (E\!\ggg \!25)}$

${\displaystyle \color {red}\boxplus }$

С публикацией FIPS PUB 180-2 NIST добавил три дополнительные хэш-функции в семейство SHA. Алгоритмы известны под общим названием SHA-2, по названию их длины дайджеста (в битах): SHA-256, SHA-384 и SHA-512.

Алгоритмы были впервые опубликованы в 2001 году в проекте FIPS PUB 180-2, в то время были приняты публичные обзоры и комментарии. В августе 2002 года FIPS PUB 180-2 стал новым стандартом Secure Hash , заменив FIPS PUB 180-1, выпущенный в апреле 1995 года. Обновленный стандарт включал оригинальный алгоритм SHA-1 с обновленной технической нотацией, соответствующей описанию внутренней работы семейства SHA-2. ^[4]

В феврале 2004 года было опубликовано уведомление об изменении для FIPS PUB 180-2, в котором был указан дополнительный вариант, SHA-224, определенный для соответствия длине ключа двухключевого Triple DES . ^[7] В октябре 2008 года стандарт был обновлен в FIPS PUB 180-3, включая SHA-224 из уведомления об изменении, но в остальном не внося никаких фундаментальных изменений в стандарт. Основной мотивацией для обновления стандарта было перемещение информации о безопасности об алгоритмах хэширования и рекомендаций по их использованию в Специальные публикации 800-107 и 800-57. ^{[8] [9] [10]} Подробные тестовые данные и примеры дайджестов сообщений также были удалены из стандарта и предоставлены в виде отдельных документов. ^[11]

В январе 2011 года NIST опубликовал SP800-131A, в котором был указан переход от действующего на тот момент минимума в 80 бит безопасности (обеспечиваемого SHA-1), допустимого для использования федеральным правительством до конца 2013 года, к 112 бит безопасности (обеспечиваемой SHA-2), являющейся как минимальным требованием (начиная с 2014 года), так и рекомендуемым уровнем безопасности (начиная с даты публикации в 2011 году). ^[12]

В марте 2012 года стандарт был обновлен в FIPS PUB 180-4, добавив хэш-функции SHA-512/224 и SHA-512/256, и описав метод генерации начальных значений для усеченных версий SHA-512. Кроме того, было снято ограничение на заполнение входных данных перед вычислением хэша, что позволило вычислять хэш-данные одновременно с генерацией контента, такого как видео или аудиопоток в реальном времени. Заполнение конечного блока данных все равно должно происходить до вывода хэша. ^[13]

В июле 2012 года NIST пересмотрел SP800-57, который содержит руководство по управлению криптографическими ключами. Публикация запретила создание цифровых подписей с хэш-безопасностью ниже 112 бит после 2013 года. Предыдущая редакция от 2007 года указывала конец 2010 года. ^[10] В августе 2012 года NIST пересмотрел SP800-107 таким же образом. ^[9]

В 2012 году на конкурсе хэш-функций NIST была выбрана новая хэш-функция SHA-3 . ^[14] Алгоритм SHA-3 не является производным от SHA-2.

Приложения

Функция хэширования SHA-2 реализована в некоторых широко используемых приложениях и протоколах безопасности, включая TLS и SSL , PGP , SSH , S/MIME и IPsec . Собственная вычислительная потребность алгоритмов SHA-2 привела к предложению более эффективных решений, таких как те, которые основаны на аппаратных ускорителях специализированных интегральных схем (ASIC). ^[15]

SHA-256 используется для аутентификации пакетов программного обеспечения Debian ^[16] и в стандарте подписи сообщений DKIM ; SHA-512 является частью системы аутентификации архивного видео Международного уголовного трибунала по геноциду в Руанде . ^[17] SHA-256 и SHA-512 предложены для использования в DNSSEC . ^[18] Поставщики Unix и Linux переходят на использование 256- и 512-битного SHA-2 для безопасного хеширования паролей. ^[19]

Несколько криптовалют , включая Bitcoin , используют SHA-256 для проверки транзакций и расчета доказательства работы ^[20] или доказательства доли . ^[21] Рост числа микросхем-ускорителей ASIC SHA-2 привел к использованию схем доказательства работы на основе scrypt .

SHA-1 и SHA-2 — это алгоритмы безопасного хэширования , требуемые законом для использования в некоторых приложениях правительства США , включая использование в других криптографических алгоритмах и протоколах, для защиты конфиденциальной несекретной информации. FIPS PUB 180-1 также поощрял принятие и использование SHA-1 частными и коммерческими организациями. SHA-1 выводится из обращения для большинства правительственных целей; Национальный институт стандартов и технологий США заявляет: «Федеральные агентства должны прекратить использование SHA-1 для... приложений, требующих устойчивости к коллизиям, как только это станет практически возможным, и должны использовать семейство хэш-функций SHA-2 для этих приложений после 2010 года» (выделено в оригинале). ^[22] Директива NIST о том, что правительственные агентства США должны, но не обязаны явно, прекратить использование SHA-1 после 2010 года ^[23] , как предполагалось, ускорит переход от SHA-1.

Функции SHA-2 не были быстро приняты изначально, несмотря на лучшую безопасность, чем SHA-1. Причины могут включать отсутствие поддержки SHA-2 в системах под управлением Windows XP SP2 или более ранних версий ^[24] и отсутствие воспринимаемой срочности, поскольку коллизии SHA-1 еще не были обнаружены. Команда Google Chrome объявила о плане постепенного прекращения поддержки их веб-браузером сертификатов TLS, зависящих от SHA-1, в течение периода с конца 2014 года и начала 2015 года. ^{[25] [26] [27]} Аналогичным образом, Microsoft объявила ^[28] , что Internet Explorer и Edge прекратят поддерживать публичные сертификаты TLS, подписанные SHA-1, с февраля 2017 года. Mozilla отключила SHA-1 в начале января 2016 года, но была вынуждена временно включить его через обновление Firefox после проблем с веб-интерфейсами пользователя некоторых моделей маршрутизаторов и устройств безопасности . ^[29]

Криптоанализ и проверка

Для хэш-функции, для которой L — это число бит в дайджесте сообщения , нахождение сообщения, соответствующего данному дайджесту сообщения, всегда можно выполнить с помощью поиска методом перебора за 2 ^L оценок. Это называется атакой прообраза и может быть или не быть практичным в зависимости от L и конкретной вычислительной среды. Второй критерий, нахождение двух разных сообщений, которые производят один и тот же дайджест сообщения, известный как столкновение , требует в среднем только 2 ^{L /2} оценок с использованием атаки дня рождения .

Некоторые приложения, использующие криптографические хэши, такие как хранилище паролей, лишь в минимальной степени подвержены атаке коллизии . Создание пароля, который работает для данной учетной записи, требует атаки прообраза, а также доступа к хэшу исходного пароля (обычно в файле shadow), что может быть или не быть тривиальным. Обратное шифрование пароля (например, для получения пароля для попытки взломать учетную запись пользователя в другом месте) не становится возможным из-за атак. (Однако даже безопасный хэш пароля не может предотвратить атаки методом подбора на слабые пароли .)

В случае подписания документа злоумышленник не мог просто подделать подпись существующего документа — злоумышленнику пришлось бы создать пару документов, один безобидный и один вредоносный, и заставить владельца закрытого ключа подписать безобидный документ. Существуют практические обстоятельства, в которых это возможно; до конца 2008 года можно было создавать поддельные SSL- сертификаты с использованием коллизии MD5 , которые принимались бы широко используемыми веб-браузерами. ^[30]

Повышенный интерес к криптографическому хэш-анализу во время соревнования SHA-3 породил несколько новых атак на семейство SHA-2, лучшие из которых приведены в таблице ниже. Только атаки коллизий имеют практическую сложность; ни одна из атак не распространяется на полную раундовую хэш-функцию.

На конференции FSE 2012 исследователи из Sony выступили с докладом, в котором предположили, что атаки псевдоколлизий могут быть расширены до 52 раундов на SHA-256 и до 57 раундов на SHA-512, основываясь на атаке с бикликовым псевдопрообразом. ^[31]

Официальное подтверждение

Реализации всех функций безопасности, одобренных FIPS, могут быть официально проверены с помощью программы CMVP , совместно проводимой Национальным институтом стандартов и технологий (NIST) и Communications Security Establishment (CSE). Для неформальной проверки пакет для генерации большого количества тестовых векторов доступен для загрузки на сайте NIST; полученная проверка, однако, не заменяет формальную проверку CMVP, которая требуется по закону ^{[ требуется ссылка ]} для определенных приложений.

По состоянию на декабрь 2013 года ^{[обновлять]}существует более 1300 проверенных реализаций SHA-256 и более 900 реализаций SHA-512, при этом только 5 из них способны обрабатывать сообщения с длиной в битах, не кратной восьми, при этом поддерживая оба варианта. ^[40]

Тестовые векторы

Хэш-значения пустой строки (т.е. входного текста нулевой длины).

SHA224("")0x d14a028c2a3a2bc9476102bb288234c415a2b01f828ea62ac5b3e42fSHA256("")0x e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855SHA384("")0x 38b060a751ac96384cd9327eb1b1e36a21fdb71114be07434c0cc7bf63f6e1da274edebfe76f65fbd51ad2f14898b95bSHA512("")0x cf83e1357eefb8bdf1542850d66d8007d620e4050b5715dc83f4a921d36ce9ce 47d0d13c5d85f2b0ff8318d2877eec2f63b931bd47417a81a538327af927da3eSHA512/224("")0x 6ed0dd02806fa89e25de060c19d3ac86cabb87d6a0ddd05c333b84f4SHA512/256("")0x c672b8d1ef56ed28ab87c3622c5114069bdd3ad7b8f9737498d0c01ecef0967a

Даже небольшое изменение в сообщении (с подавляющей вероятностью) приведет к другому хешу из-за эффекта лавины . Например, добавление точки в конец следующего предложения изменяет примерно половину (111 из 224) битов в хеше, что эквивалентно выбору нового хеша наугад:

SHA224(" Быстрая коричневая лиса перепрыгивает через ленивую собаку ")0x 730e109bd7a8a32b1cb9d9a09aa2325d2430587ddbc0c38bad911525SHA224(" Быстрая коричневая лиса перепрыгивает через ленивую собаку . ")0x 619cba8e8e05826e9b8c519c0a5c68f4fb653e8a3d8aa04bb2c8cd4c

Псевдокод

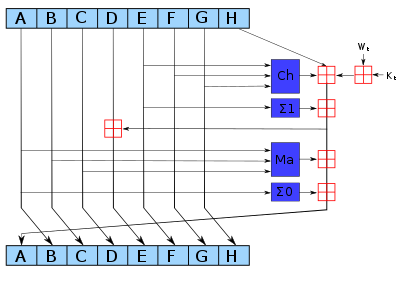
Ниже приведен псевдокод для алгоритма SHA-256. Обратите внимание на значительное увеличение смешивания между битами слов w[16..63]по сравнению с SHA-1.

Примечание 1: Все переменные являются 32-битными целыми числами без знака, а сложение вычисляется по модулю 2 32. Примечание 2: Для каждого раунда существует одна константа раунда k[i] и одна запись в массиве расписания сообщений w[i], 0 ≤ i ≤ 63. Примечание 3: Функция сжатия использует 8 рабочих переменных, от a до h. Примечание 4: При выражении констант в этом псевдокоде и при разборе данных блока сообщения из байтов в слова используется соглашение о порядке байтов от старшего к младшему, например, первое слово входного сообщения "abc" после заполнения равно 0x61626380.  Инициализируем хеш-значения: (первые 32 бита дробных частей квадратных корней первых 8 простых чисел 2..19):h0 := 0x6a09e667h1 := 0xbb67ae85h2 := 0x3c6ef372h3 := 0xa54ff53ah4 := 0x510e527fh5 := 0x9b05688ch6 := 0x1f83d9abh7 := 0x5be0cd19Инициализируем массив раундовых констант: (первые 32 бита дробных частей кубических корней первых 64 простых чисел 2..311):к[0..63] := 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5, 0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174, 0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da, 0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967, 0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85, 0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070, 0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3, 0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2Предварительная обработка (заполнение):начать с исходного сообщения длиной L битдобавить один бит «1»добавить K битов «0», где K — минимальное число >= 0, такое, что (L + 1 + K + 64) кратно 512добавить L как 64-битное целое число с обратным порядком байтов, делая общую длину после обработки кратной 512 битамтаким образом, что биты в сообщении будут следующими: <исходное сообщение длиной L> 1 <K нулей> <L как 64-битное целое число> , (количество бит будет кратно 512)Обрабатываем сообщение последовательными 512-битными фрагментами:разбить сообщение на 512-битные фрагментыдля каждого куска создать массив расписания сообщений из 64 записей w[0..63] из 32-битных слов (Начальные значения в w[0..63] не имеют значения, поэтому многие реализации обнуляют их здесь) копировать фрагмент в первые 16 слов w[0..15] массива расписания сообщений Расширить первые 16 слов до оставшихся 48 слов w[16..63] массива расписания сообщений:  для i от 16 до 63 s0 := (w[i-15] поворот вправо 7) xor (w[i-15] поворот вправо 18) xor (w[i-15] сдвиг вправо 3) s1 := (w[i-2] поворот вправо 17) xor (w[i-2] поворот вправо 19) xor (w[i-2] сдвиг вправо 10) w[i] := w[i-16] + s0 + w[i-7] + s1 Инициализируйте рабочие переменные текущим значением хэша: а := h0 б := h1 с := h2 д := х3 е := h4 ф := h5 г := h6 ч := ч7 Основной цикл функции сжатия:  для i от 0 до 63 S1 := (e поворот вправо 6) xor (e поворот вправо 11) xor (e поворот вправо 25) ch := (e и f) xor (( не e) и g) temp1 := h + S1 + ch + k[i] + w[i] S0 := (поворот вправо 2) xor (поворот вправо 13) xor (поворот вправо 22) maj := (a и b) xor (a и c) xor (b и c) темп2 := S0 + маж  ч := г г := ф ф := е е := d + темп1 д := с с := б б := а а := темп1 + темп2 Добавить сжатый фрагмент к текущему значению хеша: h0 := h0 + a h1 := h1 + b h2 := h2 + с h3 := h3 + d h4 := h4 + е х5 := х5 + ф h6 := h6 + г h7 := h7 + hВывести окончательное значение хэша (от старшего к младшему):
digest := hash := h0 append h1 append h2 append h3 append h4 append h5 append h6 append h7

Вычисление значений chи majможно оптимизировать так же , как описано для SHA-1 .

SHA-224 идентичен SHA-256, за исключением того, что:

• начальные значения хэша h0различаются h7, и
• вывод формируется путем пропускания h7.

Начальные значения хэша SHA-224 (в прямом порядке байтов): (Вторые 32 бита дробных частей квадратных корней простых чисел с 9-го по 16-е 23..53)ч[0..7] := 0xc1059ed8, 0x367cd507, 0x3070dd17, 0xf70e5939, 0xffc00b31, 0x68581511, 0x64f98fa7, 0xbefa4fa4

SHA-512 по структуре идентичен SHA-256, но:

• сообщение разбивается на 1024-битные фрагменты,
• начальные значения хэша и константы раунда расширены до 64 бит,
• вместо 64 раундов 80,
• массив расписания сообщений w имеет 80 64-битных слов вместо 64 32-битных слов,
• для расширения массива расписания сообщений w цикл выполняется от 16 до 79 вместо от 16 до 63,
• раундовые константы основаны на первых 80 простых числах 2..409,
• размер слова, используемого для вычислений, составляет 64 бита,
• добавленная длина сообщения (до предварительной обработки) в битах представляет собой 128-битное целое число с обратным порядком байтов, и
• используемые величины сдвига и поворота различны.

Начальные значения хэша SHA-512 (в обратном порядке байтов):h[0..7] := 0x6a09e667f3bcc908, 0xbb67ae8584caa73b, 0x3c6ef372fe94f82b, 0xa54ff53a5f1d36f1, 0x510e527fade682d1, 0x9b05688c2b3e6c1f, ​​0x1f83d9abfb41bd6b, 0x5be0cd19137e2179Константы раунда SHA-512:к[0..79] := 0x428a2f98d728ae22, 0x7137449123ef65cd, 0xb5c0fbcfec4d3b2f, 0xe9b5dba58189dbbc, 0x3956c25bf348b538, 0x59f111f1b605d019, 0x923f82a4af194f9b, 0xab1c5ed5da6d8118, 0xd807aa98a3030242, 0x12835b0145706fbe, 0x243185be4ee4b28c, 0x550c7dc3d5ffb4e2, 0x72be5d74f27b896f, 0x80deb1fe3b1696b1, 0x9bdc06a725c71235, 0xc19bf174cf692694, 0xe49b69c19ef14ad2, 0xefbe4786384f25e3, 0x0fc19dc68b8cd5b5, 0x240ca1cc77ac9c65, 0x2de92c6f592b0275, 0x4a7484aa6ea6e483, 0x5cb0a9dcbd41fbd4, 0x76f988da831153b5, 0x983e5152ee66dfab, 0xa831c66d2db43210, 0xb00327c898fb213f, 0xbf597fc7beef0ee4, 0xc6e00bf33da88fc2, 0xd5a79147930aa725, 0x06ca6351e003826f, 0x142929670a0e6e70, 0x27b70a8546d22ffc, 0x2e1b21385c26c926, 0x4d2c6dfc5ac42aed, 0x53380d139d95b3df, 0x650a73548baf63de, 0x766a0abb3c77b2a8, 0x81c2c92e47edaee6, 0x92722c851482353b, 0xa2bfe8a14cf10364, 0xa81a664bbc423001, 0xc24b8b70d0f89791, 0xc76c51a30654be30, 0xd192e819d6ef5218, 0xd69906245565a910, 0xf40e35855771202a, 0x106aa07032bbd1b8, 0x19a4c116b8d2d0c8, 0x1e376c085141ab53, 0x2748774cdf8eeb99, 0x34b0bcb5e19b48a8, 0x391c0cb3c5c95a63, 0x4ed8aa4ae3418acb, 0x5b9cca4f7763e373, 0x682e6ff3d6b2b8a3, 0x748f82ee5defb2fc, 0x78a5636f43172f60, 0x84c87814a1f0ab72, 0x8cc702081a6439ec, 0x90befffa23631e28, 0xa4506cebde82bde9, 0xbef9a3f7b2c67915, 0xc67178f2e372532b, 0xca273eceea26619c, 0xd186b8c721c0c207, 0xeada7dd6cde0eb1e, 0xf57d4f7fee6ed178, 0x06f067aa72176fba, 0x0a637dc5a2c898a6, 0x113f9804bef90dae, 0x1b710b35131c471b, 0x28db77f523047d84, 0x32caab7b40c72493, 0x3c9ebe0a15c9bebc, 0x431d67c49c100d4c, 0x4cc5d4becb3e42b6, 0x597f299cfc657e2a, 0x5fcb6fab3ad6faec, 0x6c44198c4a475817Сумма и сигма SHA-512:S0 := (поворот вправо 28) xor (поворот вправо 34) xor (поворот вправо 39)S1 := (e поворот вправо 14) xor (e поворот вправо 18) xor (e поворот вправо 41)s0 := (w[i-15] поворот вправо 1) xor (w[i-15] поворот вправо 8) xor (w[i-15] сдвиг вправо 7)s1 := (w[i-2] поворот вправо 19) xor (w[i-2] поворот вправо 61) xor (w[i-2] сдвиг вправо 6)

SHA-384 идентичен SHA-512, за исключением того, что:

• начальные значения хэш- h0функции h7различаются (взяты с 9-го по 16-е простые числа), и
• вывод строится путем исключения h6и h7.

Начальные значения хэша SHA-384 (в обратном порядке байтов):h[0..7] := 0xcbbb9d5dc1059ed8, 0x629a292a367cd507, 0x9159015a3070dd17, 0x152fecd8f70e5939, 0x67332667ffc00b31, 0x8eb44a8768581511, 0xdb0c2e0d64f98fa7, 0x47b5481dbefa4fa4

SHA-512/t идентичен SHA-512, за исключением того, что:

• начальные значения хэша h0задаются h7функцией генерации SHA-512/t IV ,
• выходной сигнал формируется путем усечения конкатенации h0через th7 битов ,
• t равное 384 не допускается, вместо этого следует использовать SHA-384, как указано, и
• Значения t 224 и 256 особо отмечены как одобренные.

Функция генерации SHA-512/t IV оценивает модифицированный SHA-512 на строке ASCII "SHA-512/ t ", замененной десятичным представлением t . Модифицированный SHA-512 такой же, как SHA-512, за исключением того, что его начальные значения h0по h7были подвергнуты операции XOR с шестнадцатеричной константой 0xa5a5a5a5a5a5a5a5.

Пример реализации семейства хэш-функций SHA-2 на языке C можно найти в RFC 6234.

Сравнение функций SHA

В таблице ниже внутреннее состояние означает «внутреннюю хеш-сумму» после каждого сжатия блока данных.

В столбце побитовых операций "Rot" означает поворот без переноса , а "Shr" означает правый логический сдвиг . Все эти алгоритмы используют модульное сложение в той или иной форме, за исключением SHA-3.

Более подробные измерения производительности современных архитектур процессоров приведены в таблице ниже.

Показатели производительности, обозначенные как «x86», работали с использованием 32-битного кода на 64-битных процессорах, тогда как показатели «x86-64» являются собственным 64-битным кодом. Хотя SHA-256 разработан для 32-битных вычислений, он выигрывает от кода, оптимизированного для 64-битных процессоров на архитектуре x86. 32-битные реализации SHA-512 значительно медленнее своих 64-битных аналогов. Варианты обоих алгоритмов с разными размерами выходных данных будут работать одинаково, поскольку функции расширения и сжатия сообщений идентичны, и различаются только начальные значения хэш-функции и размеры выходных данных. Лучшие реализации MD5 и SHA-1 выполняют от 4,5 до 6 циклов на байт на современных процессорах.

Тестирование проводилось в Иллинойсском университете в Чикаго на их системе hydra8, работающей на Intel Xeon E3-1275 V2 с тактовой частотой 3,5 ГГц, и на их системе hydra9, работающей на AMD A10-5800K APU с тактовой частотой 3,8 ГГц. ^[46] Указанные выше скорости циклов на байт являются средней производительностью алгоритма, обрабатывающего сообщение размером 4096 байт с использованием криптографического бенчмаркингового программного обеспечения SUPERCOP. ^[47] Производительность в МиБ/с экстраполируется из тактовой частоты ЦП на одном ядре; реальная производительность будет варьироваться из-за множества факторов.

Реализации

Ниже приведен список криптографических библиотек, поддерживающих SHA-2:

• Ботан
• Надувной замок
• Криптлиб
• Крипто++
• Libgcrypt
• Mbed TLS ^{[48] [49]}
• либсодиум
• Крапива
• LibreSSL
• OpenSSL
• GnuTLS
• wolfSSL

Аппаратное ускорение обеспечивается следующими расширениями процессора:

• Расширения Intel SHA : доступны на некоторых процессорах Intel и AMD x86.
• ЧЕРЕЗ PadLock
• Расширения криптографии ARMv8 ^[50]
• IBM z/Architecture : Доступно с 2005 года как часть Message-Security-Assist Extensions 1 (SHA-256) и 2 (SHA-512) ^[51]
• IBM Power ISA начиная с версии 2.07

Смотрите также

• Сравнение криптографических хеш-функций
• Сравнение криптографических библиотек
• Резюме безопасности хэш-функции
• Хэшкэш
• HMAC
• Международная ассоциация криптологических исследований (IACR)
• Надежная временная метка

Ссылки

1. Дмитрий Ховратович, Кристиан Рехбергер и Александра Савельева (2011). "Bicliques for Proimages: Attacks on Skein-512 and the SHA-2 family" (PDF) . Архив IACR Cryptology ePrint . 2011 (286). Архивировано (PDF) из оригинала 2022-02-15 . Получено 2022-02-15 .
2. Марио Ламбергер и Флориан Мендель (2011). "Higher-Order Differential Attack on Reduced SHA-256" (PDF) . Архив IACR Cryptology ePrint . 2011 (37). Архивировано (PDF) из оригинала 2022-12-22 . Получено 2022-02-15 .
3. Пенард, Воутер; ван Верховен, Тим. "О семействе алгоритмов безопасного хэширования" (PDF) . staff.science.uu.nl . Архивировано из оригинала (PDF) 2016-03-30.
4. Уведомление Федерального реестра 02-21599, объявляющее об одобрении публикации FIPS 180-2 Архивировано 14 марта 2022 г. на Wayback Machine
5. "Сведения об IPR: Соединенные Штаты Америки, представленные в заявлении о генеральной лицензии Агентства национальной безопасности". IETF Datatracker . 858. Архивировано из оригинала 2016-06-16 . Получено 2008-02-17 .
6. US 6829355, Лилли, Гленн М., «Устройство и метод одностороннего криптографического хеширования», опубликовано 2004-12-07, передано Агентству национальной безопасности 
7. "FIPS 180-2 с уведомлением об изменении 1" (PDF) . csrc.nist.gov . Архивировано (PDF) из оригинала 2017-08-09 . Получено 2022-02-15 .
8. Уведомление Федерального реестра E8-24743, объявляющее об одобрении публикации FIPS 180-3
9. Dang, Quynh (2012-08-24). Рекомендация для приложений, использующих одобренные алгоритмы хэширования (отчет). Национальный институт стандартов и технологий. Архивировано из оригинала 2023-08-28 . Получено 2023-08-28 .
10. Баркер, Элейн; Баркер, Уильям; Берр, Уильям; Полк, У.; Смид, Майлз (2012-07-10). Рекомендации по управлению ключами, часть 1: Общие положения (пересмотр 3) (отчет). Национальный институт стандартов и технологий. Архивировано из оригинала 28.08.2023 . Получено 28.08.2023 .
11. "NIST.gov – Computer Security Division – Computer Security Resource Center". 29 декабря 2016 г. Архивировано из оригинала 9 сентября 2017 г. Получено 15 февраля 2022 г.
12. Баркер, Элейн; Рогински, Аллен (2011-01-13). Переходы: Рекомендации по переходу на использование криптографических алгоритмов и длин ключей (Отчет). Национальный институт стандартов и технологий. Архивировано из оригинала 2023-08-28 . Получено 2023-08-28 .
13. Уведомление Федерального регистра 2012-5400, объявляющее об одобрении публикации FIPS 180-4
14. "NIST выбирает победителя конкурса Secure Hash Algorithm (SHA-3)". NIST . 2 октября 2012 г. Архивировано из оригинала 2 апреля 2015 г. Получено 24 февраля 2015 г.
15. Лукас Даудт Франк; Габриэль Аугусто Гинья; Жоау Паулу Карму; Хосе А. Афонсо; Максимилиам Луппе (2024). «Индивидуальная разработка ASIC для SHA-256 с использованием инструментов с открытым исходным кодом». Компьютеры . 13 (1): 9. doi : 10.3390/computers13010009 . hdl : 1822/89307 .
16. "Проверка подлинности образов Debian". Архивировано из оригинала 2024-02-19 . Получено 2024-02-19 .
17. Маркофф, Джон (27.01.2009). «Инструмент для проверки цифровых записей, даже в условиях смены технологий». The New York Times . ISSN  0362-4331. Архивировано из оригинала 19.09.2023 . Получено 27.08.2023 .
18. Использование алгоритмов SHA-2 с RSA в записях ресурсов DNSKEY и RRSIG для DNSSEC. Октябрь 2009 г. doi : 10.17487/RFC5702 . RFC 5702.
19. "Unix crypt with SHA-256/512". akkadia.org . Архивировано из оригинала 2023-08-20 . Получено 27-08-2023 .
20. Bitcoin, Surplus. «Биткойн не тратит энергию». Surplus Bitcoin . Архивировано из оригинала 2022-05-28 . Получено 2020-04-20 .
21. "Что такое SHA-256 и как он связан с биткоином? - Mycryptopedia". Mycryptopedia . 2017-09-21. Архивировано из оригинала 2018-09-17 . Получено 2018-09-17 .
22. Отдел компьютерной безопасности, Лаборатория информационных технологий (2017-01-04). "Политика NIST в отношении хэш-функций – Хэш-функции | CSRC | CSRC". CSRC | NIST . Архивировано из оригинала 28-08-2023 . Получено 27-08-2023 .
23. "Безопасное хеширование". NIST . Архивировано из оригинала 2011-06-25 . Получено 2010-11-25 .
24. "Обзор Windows XP Service Pack 3" (PDF) . Корпорация Microsoft. Архивировано из оригинала (PDF) 30 мая 2008 г.
25. "Постепенное прекращение работы SHA-1". Блог Chromium . Архивировано из оригинала 2023-08-07 . Получено 2023-08-27 .
26. Эрик Милл. "SHAAAAAAAAAAAAA". SHAAAAAAAAAAAAA.com . Архивировано из оригинала 2017-03-01 . Получено 2015-08-26 .
27. "Часто задаваемые вопросы об устаревании SHA1 в Chrome". Филиппо Вальсорда . 2015-04-08. Архивировано из оригинала 2023-08-28 . Получено 2023-08-27 .
28. "Обновление нашей дорожной карты устаревания SHA-1 – Блог разработчиков Microsoft EdgeБлог разработчиков Microsoft Edge". blogs.windows.com . 29 апреля 2016 г. Архивировано из оригинала 28.11.2016 . Получено 28.11.2016 .
29. онлайн, Хайзе (08 января 2016 г.). «Firefox: Mozilla использует SHA-1 ab… und Direct Wieder An». Безопасность (на немецком языке). Архивировано из оригинала 28 августа 2023 г. Проверено 27 августа 2023 г.
30. Александр Сотиров, Марк Стивенс, Джейкоб Аппельбаум, Арьен Ленстра, Дэвид Молнар, Даг Арне Освик, Бенне де Вегер, MD5 сегодня считается вредоносным: создание мошеннического сертификата CA. Архивировано 23 марта 2022 г. на Wayback Machine , дата обращения 29 марта 2009 г.
31. Цзи Ли, Таканори Исобе и Кёдзи Шибутани, Sony China Research Laboratory и Sony Corporation, Преобразование атаки Meet-in-the-Middle Proimage в атаку Pseudo Collision: применение к SHA-2. Архивировано 24 февраля 2022 г. на Wayback Machine.
32. Санадхья, Сомитра Кумар; Саркар, Палаш (2008), Новые атаки столкновений против 24-шагового SHA-2, Lecture Notes in Computer Science, т. 5365, Springer-Verlag, стр. 91–103, doi :10.1007/978-3-540-89754-5_8, ISBN 978-3-540-89753-8, заархивировано из оригинала 21.01.2022 , извлечено 12.02.2024
33. Санадхья, Сомитра Кумар; Саркар, Палаш (2009). «Комбинаторный анализ недавних атак на семейство алгоритмов SHA-2 с уменьшенным шагом». Криптография и коммуникации . doi :10.1007/s12095-009-0011-5. Архивировано из оригинала 2023-08-02 . Получено 2024-02-12 .
34. Kazumaro Aoki; Jian Guo; Krystian Matusiewicz; Yu Sasaki & Lei Wang (2009). "Прообразы для Step-Reduced SHA-2". Advances in Cryptology – ASIACRYPT 2009. Lecture Notes in Computer Science. Vol. 5912. Springer Berlin Heidelberg. pp. 578–597. doi :10.1007/978-3-642-10366-7_34. ISBN 978-3-642-10366-7. ISSN  0302-9743.
35. Цзянь Го; Сань Лин; Кристиан Рехбергер и Хуасюн Ван (2010). «Расширенные атаки на прообразы Meet-in-the-Middle: первые результаты по Full Tiger и улучшенные результаты по MD4 и SHA-2». Достижения в криптологии — ASIACRYPT 2010 (PDF) . Конспект лекций по информатике. Том 6477. Springer Berlin Heidelberg. С. 56–75. doi :10.1007/978-3-642-17373-8_4. ISBN 978-3-642-17373-8. ISSN  0302-9743. Архивировано (PDF) из оригинала 2022-03-03 . Получено 2022-02-15 .
36. Флориан Мендель; Томислав Над; Мартин Шлеффер (2013). «Улучшение локальных коллизий: новые атаки на сокращенный SHA-256». Достижения в криптологии – EUROCRYPT 2013. Конспект лекций по информатике. Том 7881. Springer Berlin Heidelberg. С. 262–278. doi :10.1007/978-3-642-38348-9_16. ISBN 978-3-642-38348-9. ISSN  0302-9743. Архивировано из оригинала 2018-11-06 . Получено 2014-12-13 .
37. Мария Эйхлзедер и Флориан Мендель и Мартин Шлеффер (2014). «Ветвление эвристики в дифференциальном поиске коллизий с приложениями к SHA-512» (PDF) . Архив IACR Cryptology ePrint . 2014 (302). Архивировано (PDF) из оригинала 2022-01-20 . Получено 15-02-2022 .
38. Кристоф Добрауниг; Мария Эйхлзедер и Флориан Мендель (2016). "Анализ SHA-512/224 и SHA-512/256" (PDF) . Международная ассоциация криптологических исследований . Архивировано (PDF) из оригинала 2017-07-15 . Получено 2016-04-15 .
39. Ли, Инсинь; Лю, Фукан; Ван, Гаоли (2024). «Новые записи в атаках с коллизиями на SHA-2». Архив Cryptology ePrint . Архивировано из оригинала 2024-03-02 . Получено 2024-03-02 .
40. "SHS Validation List". NIST . 2017-06-16. Архивировано из оригинала 2017-06-17.
41. "Таблица измерений". bench.cr.yp.to .
42. Тао, Се; Лю, Фаньбао; Фэн, Дэнго (2013). Быстрая коллизионная атака на MD5 (PDF) . Архив Cryptology ePrint (технический отчет). IACR .
43. Стивенс, Марк ; Бурштейн, Эли ; Карпман, Пьер; Альбертини, Анж; Марков, Ярик. Первое столкновение для полного SHA-1 (PDF) (Технический отчет). Google Research .
    • Марк Стивенс; Эли Бурштейн; Пьер Карпман; Анж Альбертини; Ярик Марков; Алекс Пети Бьянко; Клемент Бейсс (23 февраля 2017 г.). «Анонс первой коллизии SHA1». Блог безопасности Google .
44. Без усечения полное внутреннее состояние хэш-функции известно, независимо от устойчивости к коллизиям. Если вывод усечен, удаленная часть состояния должна быть найдена, прежде чем хэш-функция может быть возобновлена, что позволяет продолжить атаку.
45. "Семейство функций губки Кеккака" . Получено 27.01.2016 .
46. SUPERCOP Benchmarks Измерения хэш-функций, индексированных машиной
47. "SUPERCOP". Архивировано из оригинала 15 февраля 2015 года . Получено 24 февраля 2015 года .
48. "Поддерживаемые наборы шифров SSL / TLS". Архивировано из оригинала 2019-05-12 . Получено 2019-10-19 .
49. "Mbed TLS Changelog, 7 июля 2007 г.". Архивировано из оригинала 4 февраля 2019 г. Получено 19 октября 2019 г.
50. "ARM Cortex-A53 MPCore Processor Technical Reference Manual Cryptography Extension". Архивировано из оригинала 2020-06-01 . Получено 2022-02-15 .
51. IBM z/Architecture Principles of Operation, номер публикации SA22-7832. См. инструкции KIMD и KLMD в Главе 7.

Дальнейшее чтение

• Анри Жильбер, Хелена Хандшу: Анализ безопасности SHA-256 и сестер. Избранные области в криптографии 2003: стр. 175–193
• «Предлагаемая редакция Федерального стандарта обработки информации (FIPS) 180, Стандарт безопасного хэширования». Федеральный реестр . 59 (131): 35317–35318. 11 июля 1994 г. Архивировано из оригинала 28 июля 2020 г. Получено 26 апреля 2007 г.

Внешние ссылки

• Описания SHA-256, SHA-384 и SHA-512 от NIST
• SHA-2 Checker – SHAChecker для проверки совместимости SSL с SHA-2
• Калькулятор SHA-256 – Калькулятор SHA-256
• Генератор хэшей SHA-256 – Генератор SHA256 – Также обслуживает другие критически важные безопасные алгоритмы хэширования
• Спецификации для стандарта безопасного хэширования (SHS) – проект предлагаемого SHS (SHA-0)
• Стандарт безопасного хэширования (SHS) – Предлагаемый SHS (SHA-0)
• CSRC Cryptographic Toolkit – Официальный сайт NIST для стандарта Secure Hash
• FIPS PUB 180-4: Secure Hash Standard (SHS) ( PDF , 834 КБ) – Текущая версия Secure Hash Standard (SHA-1, SHA-224, SHA-256, SHA-384 и SHA-512), август 2015 г.
• Тестовые векторы для SHA-256/384/512 из проекта NESSIE
• Тестовые векторы для SHA-1, SHA-2 с сайта NIST
• Проект криптографического хэша NIST – конкурс SHA-3
• RFC 3874: «224-битная односторонняя хэш-функция: SHA-224»
• RFC 6234: «Алгоритмы безопасного хэширования США (SHA и HMAC и HKDF на основе SHA)»; содержит пример реализации на языке C
• Демонстрация алгоритма SHA-256