Анализ кумулятивной частоты — это анализ частоты появления значений явления, меньших контрольного значения. Явление может зависеть от времени или пространства. Кумулятивная частота также называется частотой непревышения .
Анализ кумулятивной частоты выполняется для получения информации о том, как часто определенное явление (характеристика) находится ниже определенного значения. Это может помочь в описании или объяснении ситуации, в которой участвует явление, или в планировании вмешательств, например, в защиту от наводнений. [1]
Этот статистический метод можно использовать для того, чтобы увидеть, насколько вероятно, что событие, например, наводнение, повторится в будущем, основываясь на том, как часто оно случалось в прошлом. Его можно адаптировать для учета таких вещей, как изменение климата, вызывающее более влажные зимы и более сухое лето.
Частотный анализ [2] — это анализ того, как часто или насколько часто наблюдаемое явление происходит в определенном диапазоне.
Частотный анализ применяется к записи длины N наблюдаемых данных X 1 , X 2 , X 3 . . . X N по изменчивому явлению X. Запись может зависеть от времени (например, количество осадков, измеренное в одном месте) или пространства (например, урожайность в районе) или иным образом.
Кумулятивная частота M Xr эталонного значения Xr — это частота, с которой наблюдаемые значения X меньше или равны Xr .
Относительную кумулятивную частоту Fc можно рассчитать по формуле:
где N — количество данных
Кратко это выражение можно записать так:
Когда Xr = X min , где X min — уникальное минимальное наблюдаемое значение, обнаруживается, что Fc = 1/ N , поскольку M = 1 . С другой стороны, когда Xr = X max , где X max — уникальное максимальное наблюдаемое значение, обнаруживается, что Fc = 1 , поскольку M = N . Следовательно, когда Fc = 1 , это означает, что Xr — это значение, при котором все данные меньше или равны Xr .
В процентах уравнение выглядит так:
Кумулятивную вероятность Pc того , что X будет меньше или равно Xr, можно оценить несколькими способами на основе кумулятивной частоты M.
Один из способов — использовать относительную кумулятивную частоту Fc в качестве оценки.
Другой способ — учесть возможность того, что в редких случаях X может принимать значения, превышающие наблюдаемый максимум X max . Это можно сделать, разделив кумулятивную частоту M на N +1 вместо N . Тогда оценка становится:
Существуют также другие предложения по знаменателю (см. положения графиков ).
Оценка вероятности упрощается путем ранжирования данных.
Когда наблюдаемые данные X расположены в порядке возрастания ( X 1 ≤ X 2 ≤ X 3 ≤ ⋯ ≤ X N , минимум первый, а максимум последний), а Ri — это ранговый номер наблюдения Xi , где приставка i указывает на порядковый номер в диапазоне возрастающих данных, то кумулятивную вероятность можно оценить следующим образом:
С другой стороны, когда наблюдаемые данные из X расположены в порядке убывания , максимум первым, а минимум последним, а Rj — это номер ранга наблюдения Xj , кумулятивную вероятность можно оценить следующим образом:

Чтобы представить кумулятивное распределение частот как непрерывное математическое уравнение вместо дискретного набора данных, можно попытаться подогнать кумулятивное распределение частот к известному кумулятивному распределению вероятностей. [2] [3]
В случае успеха известного уравнения достаточно, чтобы сообщить о распределении частот, и таблица данных не потребуется. Кроме того, уравнение помогает интерполяции и экстраполяции. Однако следует проявлять осторожность при экстраполяции кумулятивного распределения частот, поскольку это может быть источником ошибок. Одна из возможных ошибок заключается в том, что распределение частот больше не следует выбранному распределению вероятностей за пределами диапазона наблюдаемых данных.
Любое уравнение, дающее значение 1 при интегрировании от нижнего предела до верхнего предела, хорошо согласующееся с диапазоном данных, может быть использовано в качестве распределения вероятностей для подгонки. Пример распределений вероятностей, которые могут быть использованы, можно найти в разделе распределения вероятностей .
Распределение вероятностей можно подгонять несколькими методами, [2] например:
Применение обоих типов методов с использованием, например,
часто показывает, что ряд распределений хорошо соответствуют данным и не дают существенно различающихся результатов, в то время как различия между ними могут быть небольшими по сравнению с шириной доверительного интервала. [2] Это иллюстрирует, что может быть сложно определить, какое распределение дает лучшие результаты. Например, приблизительно нормально распределенные наборы данных могут быть подогнаны под большое количество различных распределений вероятностей. [4] в то время как отрицательно перекошенные распределения могут быть подогнаны под квадратично-нормальные и зеркальные распределения Гумбеля. [5]

Иногда можно подогнать один тип распределения вероятностей к нижней части диапазона данных, а другой тип — к верхней части, разделив их точкой разрыва, благодаря чему общее соответствие улучшается.
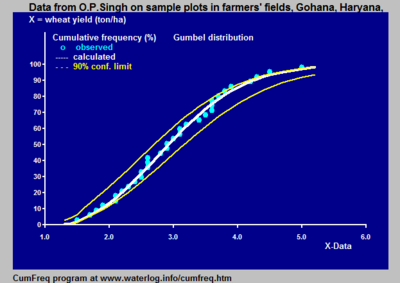
На рисунке показан пример полезного введения такого прерывистого распределения для данных об осадках в северном Перу, где климат зависит от поведения тихоокеанского течения Эль-Ниньо . Когда Ниньо простирается на юг Эквадора и входит в океан вдоль побережья Перу, климат в северном Перу становится тропическим и влажным. Когда Ниньо не достигает Перу, климат полузасушливый. По этой причине более высокие осадки следуют другому распределению частот, чем более низкие. [6]
Когда кумулятивное распределение частот выводится из записи данных, можно усомниться в том, можно ли его использовать для прогнозирования. [7] Например, если задано распределение речных сбросов за 1950–2000 годы, можно ли использовать это распределение для прогнозирования того, как часто определенный речной сброс будет превышен в 2000–50 годах? Ответ — да, при условии, что условия окружающей среды не изменятся. Если условия окружающей среды изменятся, например, изменения в инфраструктуре водораздела реки или в характере осадков из-за климатических изменений, прогноз на основе исторических записей будет подвержен систематической ошибке . Даже когда нет систематической ошибки, может быть случайная ошибка , потому что случайно наблюдаемые сбросы в течение 1950–2000 годов могли быть выше или ниже нормы, в то время как, с другой стороны, сбросы с 2000 по 2050 годы могут случайно быть ниже или выше нормы. Вопросы, связанные с этим, были исследованы в книге «Черный лебедь» .

Теория вероятностей может помочь оценить диапазон, в котором может находиться случайная ошибка. В случае кумулятивной частоты есть только две возможности: определенное опорное значение X превышено или не превышено. Сумма частоты превышения и кумулятивной частоты составляет 1 или 100%. Поэтому биномиальное распределение можно использовать для оценки диапазона случайной ошибки.
Согласно нормальной теории, биномиальное распределение можно аппроксимировать, и для больших N стандартное отклонение Sd можно рассчитать следующим образом:
где Pc — кумулятивная вероятность , а N — количество данных. Видно, что стандартное отклонение Sd уменьшается с увеличением количества наблюдений N.
Определение доверительного интервала Pc осуществляется с помощью t-критерия Стьюдента ( t ). Значение t зависит от количества данных и уровня достоверности оценки доверительного интервала. Затем нижний ( L ) и верхний ( U ) доверительные пределы Pc в симметричном распределении находятся из:
Это известно как интервал Вальда . [8] Однако биномиальное распределение симметрично относительно среднего значения только при Pc = 0,5 , но становится асимметричным и все более и более перекошенным, когда Pc приближается к 0 или 1. Поэтому, путем приближения, Pc и 1− Pc можно использовать в качестве весовых коэффициентов при назначении t.Sd для L и U :
откуда видно, что эти выражения для Pc = 0,5 такие же, как и предыдущие.

Кумулятивную вероятность Pc можно также назвать вероятностью непревышения . Вероятность превышения Pe (также называемая функцией выживания ) находится из:
Период возврата T определяется как:
и указывает ожидаемое количество наблюдений, которые необходимо провести снова , чтобы найти значение переменной в исследовании, превышающее значение, использованное для T. Верхний
( TU ) и нижний ( TL ) доверительные пределы периодов возврата можно найти соответственно как:
Для экстремальных значений исследуемой переменной U близко к 1, а небольшие изменения U вызывают большие изменения T U . Следовательно, предполагаемый период возврата экстремальных значений подвержен большой случайной ошибке. Более того, найденные доверительные интервалы справедливы для долгосрочного прогноза. Для прогнозов на более короткий срок доверительные интервалы U − L и T U − T L могут быть на самом деле шире. Вместе с ограниченной определенностью (менее 100%), используемой в t-тесте , это объясняет, почему, например, 100-летний ливень может выпадать дважды за 10 лет.

Строгое понятие периода повторяемости на самом деле имеет смысл только тогда, когда оно касается зависящего от времени явления, например, точечного выпадения осадков. Период повторяемости тогда соответствует ожидаемому времени ожидания, пока превышение не произойдет снова. Период повторяемости имеет ту же размерность, что и время, для которого каждое наблюдение является репрезентативным. Например, когда наблюдения касаются суточных осадков, период повторяемости выражается в днях, а для годовых осадков — в годах.
На рисунке показано изменение, которое может возникнуть при получении выборок переменной, которая следует определенному распределению вероятностей. Данные предоставлены Бенсоном. [1]
Полоса доверия вокруг экспериментальной кумулятивной частоты или кривой периода повторяемости дает представление о той области, в которой можно найти истинное распределение.
Кроме того, в нем разъясняется, что экспериментально найденное наиболее точное распределение вероятностей может отличаться от истинного распределения.

Наблюдаемые данные могут быть организованы в классы или группы с порядковым номером k . Каждая группа имеет нижний предел ( L k ) и верхний предел ( U k ). Когда класс ( k ) содержит m k данных, а общее количество данных равно N , то относительная частота класса или группы находится из:
или кратко:
или в процентах:
Представление всех частот классов дает распределение частот , или гистограмму . Гистограммы, даже если они сделаны из одной и той же записи, различны для разных пределов классов.
Гистограмму также можно получить из подобранного кумулятивного распределения вероятностей:
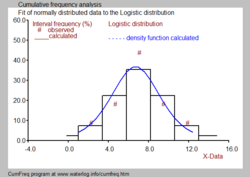
Между Fg k и Pg k может быть разница из-за отклонений наблюдаемых данных от подобранного распределения (см. синий рисунок).
Часто бывает желательно объединить гистограмму с функцией плотности вероятности , как показано на черно-белом рисунке.