Антиподальная точка

Пара диаметрально противоположных точек на окружности, сфере или гиперсфере

Две точки P и P ' (красные) являются антиподами , поскольку они являются концами диаметра PP ' , сегмента оси a ( фиолетовый), проходящего через центр сферы O (черный). P и P ' являются полюсами большого круга g (зеленый), точки которого равноудалены друг от друга (с центральным прямым углом). Любой большой круг s (синий), проходящий через полюса, является вторичным по отношению к g .

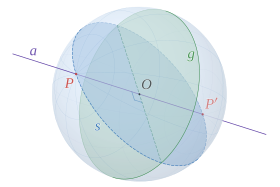
В математике две точки сферы ( или n-сферы , включая окружность ) называются антиподальными или диаметрально противоположными , если они являются концами диаметра , отрезка прямой линии между двумя точками на сфере и проходящего через ее центр . ^[1]

Для любой точки на сфере ее антиподальная точка является единственной точкой на наибольшем расстоянии , независимо от того, измеряется ли она внутренне ( расстояние по большой окружности на поверхности сферы) или внешне ( хордовое расстояние через внутреннюю часть сферы). Каждая большая окружность на сфере, проходящая через точку, также проходит через ее антиподальную точку, и существует бесконечно много больших окружностей, проходящих через пару антиподальных точек (в отличие от ситуации для любой неантиподальной пары точек, у которых есть единственная большая окружность, проходящая через обе). Многие результаты в сферической геометрии зависят от выбора неантиподальных точек и вырождаются , если антиподальные точки разрешены; например, сферический треугольник вырождается в недоопределенную луночку , если две вершины являются антиподальными.

Точка, антиподальная данной точке, называется ее антиподом , от греческого ἀντίποδες ( antípodes ), что означает «противоположные ноги»; см. Антиподы § Этимология . Иногда s опускается, и это передается как антипод , обратная формация .

Высшая математика

Концепция антиподальных точек обобщается на сферы любого измерения: две точки на сфере являются антиподальными, если они противоположны относительно центра . Каждая прямая, проходящая через центр, пересекает сферу в двух точках, по одной для каждого луча, исходящего из центра, и эти две точки являются антиподальными.

Теорема Борсука–Улама является результатом алгебраической топологии, имеющей дело с такими парами точек. Она гласит, что любая непрерывная функция из в отображает некоторую пару антиподальных точек в в ту же точку в Здесь обозначает -мерную сферу, а является -мерным вещественным координатным пространством . ${\displaystyle S^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle S^{n}}$ ${\displaystyle \mathbb {R} ^{n}.}$ ${\displaystyle S^{n}}$ ${\displaystyle n}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$

Антиподальное отображение отправляет каждую точку на сфере в ее антиподальную точку. Если точки на -сфере представлены как векторы смещения из центра сферы в евклидовом -пространстве, то две антиподальные точки представлены аддитивными обратными и и антиподальное отображение можно определить как Антиподальное отображение сохраняет ориентацию ( гомотопно тождественному отображению ) ^[2] , когда нечетно, и меняет ее на противоположную, когда четно. Его степень равна ${\displaystyle A:S^{n}\to S^{n}}$ ${\displaystyle n}$ ${\displaystyle (n+1)}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle -\mathbf {v} ,}$ ${\displaystyle A(\mathbf {x} )=-\mathbf {x} .}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle (-1)^{n+1}.}$

Если идентифицировать антиподальные точки (считающиеся эквивалентными), сфера становится моделью реального проективного пространства .

Смотрите также

• Локус разреза

Ссылки

1. Чисхолм, Хью , ред. (1911). «Антиподы»  . Encyclopaedia Britannica . Том 2 (11-е изд.). Cambridge University Press. С. 133–34.
2. В. Гийемен; А. Поллак (1974). Дифференциальная топология . Prentice-Hall.

Внешние ссылки

• «Антиподы», Энциклопедия математики , EMS Press , 2001 [1994]
• "антиподальный". PlanetMath .