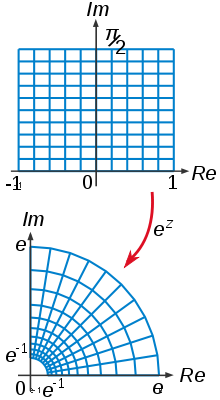
В математической теории функций одной или нескольких комплексных переменных , а также в комплексной алгебраической геометрии биголоморфизм или биголоморфная функция — это биективная голоморфная функция , обратная которой также голоморфна .
Формально, биголоморфная функция — это функция, определенная на открытом подмножестве U -мерного комплексного пространства C n со значениями в C n , которая является голоморфной и взаимно однозначной , такой, что ее образ является открытым множеством в C n , а обратное также голоморфно . В более общем случае U и V могут быть комплексными многообразиями . Как и в случае функций одной комплексной переменной, достаточным условием для того, чтобы голоморфное отображение было биголоморфным на свой образ, является то, что отображение является инъективным, и в этом случае обратное также голоморфно (например, см. Gunning 1990, Theorem I.11 or Corollary E.10 pg. 57).
Если существует биголоморфизм , мы говорим, что U и V биголоморфно эквивалентны или что они биголоморфны .
Если каждое просто связное открытое множество, отличное от всей комплексной плоскости, биголоморфно единичному кругу (это теорема об отображении Римана ). Ситуация сильно отличается в высших размерностях. Например, открытые единичные шары и открытые единичные поликруги не являются биголоморфно эквивалентными для Фактически, не существует даже собственной голоморфной функции из одного в другой.
В случае отображений f : U → C , определенных на открытом подмножестве U комплексной плоскости C , некоторые авторы (например, Freitag 2009, Definition IV.4.1) определяют конформное отображение как инъективное отображение с ненулевой производной, т. е. f '( z )≠ 0 для любого z из U . Согласно этому определению, отображение f : U → C является конформным тогда и только тогда, когда f : U → f ( U ) является биголоморфным. Обратите внимание, что согласно определению биголоморфизмов ничего не предполагается относительно их производных, поэтому эта эквивалентность содержит утверждение, что гомеоморфизм, который является комплексно дифференцируемым, должен фактически иметь ненулевую производную везде. Другие авторы (например, Conway 1978) определяют конформное отображение как отображение с ненулевой производной, но не требуя, чтобы отображение было инъективным. Согласно этому более слабому определению, конформное отображение не обязательно должно быть биголоморфным, даже если оно локально биголоморфно, например, по теореме об обратной функции. Например, если f : U → U определяется как f ( z ) = z 2 с U = C –{0}, то f конформно на U , поскольку его производная f '( z ) = 2 z ≠ 0, но оно не биголоморфно, поскольку оно равно 2-1.
В данной статье использованы материалы из биголоморфно эквивалентного сайта PlanetMath , лицензированного по лицензии Creative Commons Attribution/Share-Alike License .