Теорема о медианном избирателе в политологии и теории социального выбора , разработанная Дунканом Блэком , гласит, что если избиратели и кандидаты распределены по одномерному спектру и предпочтения избирателей имеют один пик , то любой метод голосования, совместимый с правилом большинства , выберет кандидата, которого предпочитает медианный избиратель.
Теорема была впервые сформулирована Дунканом Блэком в 1948 году. [1] Он писал, что увидел большой пробел в экономической теории относительно того, как голосование определяет исход решений, включая политические решения. Статья Блэка положила начало исследованиям того, как экономика может объяснить системы голосования. В 1957 году Энтони Даунс изложил теорему о медианном избирателе в своей книге «Экономическая теория демократии» . [2]
Сходное утверждение было сделано ранее (в 1929 году) Гарольдом Хотеллингом , который утверждал, что политики в представительной демократии будут сходиться к точке зрения медианного избирателя, [3] основывая это на своей модели экономической конкуренции . [3] [4] Однако это утверждение опирается на глубоко упрощенную модель голосования и лишь частично применимо к системам, удовлетворяющим свойству медианного избирателя. Его вообще нельзя применять к таким системам, как рейтинговое голосование по выбору (RCV) или система простого большинства , даже в двухпартийных системах. [5] [6] [примечание 1]

Теорема о медианном избирателе гласит, что в размерных выборах кандидат, наиболее близкий к медианному избирателю, является кандидатом, предпочитаемым большинством ( кандидатом Кондорсе ) , то есть кандидатом, которого большинство избирателей предпочитает всем остальным кандидатам.
В «одномерных» выборах, где мнения кандидатов и избирателей распределены по одномерному спектру, а избиратель ранжирует кандидатов по близости, так что кандидат, наиболее близкий к избирателю, получает его первое предпочтение, следующий по близости получает его второе предпочтение и т. д., теорема о медианном избирателе гласит, что «C», кандидат, наиболее близкий по взглядам к медианному избирателю «M», станет победителем по Кондорсе любых выборов, проводимых с использованием метода, удовлетворяющего критерию Кондорсе. В частности, когда есть только два кандидата, система правила большинства удовлетворяет критерию Кондорсе; для голосов за нескольких кандидатов ему удовлетворяют несколько методов.
Эскиз доказательства: Пусть медианный избиратель — Марлен. Кандидат, который ближе всего к ней, получит ее первый голос предпочтения. Предположим, что этот кандидат — Чарльз и что он находится слева от нее. Марлен и все избиратели слева от нее (по определению большинство электората) предпочтут Чарльза всем кандидатам справа от него, а Марлен и все избиратели справа от нее (тоже большинство) предпочтут Чарльза всем кандидатам слева от него. ◻
Мы скажем, что метод голосования имеет "свойство медианного избирателя в одном измерении", если он всегда выбирает кандидата, ближайшего к медианному избирателю в одномерной пространственной модели. Мы можем суммировать теорему о медианном избирателе, как утверждение, что все методы Кондорсе обладают свойством медианного избирателя в одном измерении.
Оказывается, методы Кондорсе не уникальны в этом: метод Кумбса не является последовательным по Кондорсе, но тем не менее удовлетворяет свойству медианного избирателя в одном измерении. [9] Одобрительное голосование удовлетворяет тому же свойству в рамках нескольких моделей стратегического голосования.
Невозможно полностью обобщить теорему о медианном избирателе на пространственные модели в более чем одном измерении, поскольку больше не существует единственной уникальной «медианы» для всех возможных распределений избирателей. Однако все еще возможно продемонстрировать подобные теоремы при некоторых ограниченных условиях.

Таблица показывает пример выборов, предоставленных маркизом де Кондорсе , который пришел к выводу, что это показало проблему с подсчетом Борда . [10] : 90 Победитель Кондорсе слева - это A, который предпочтительнее B на 41:40 и C на 60:21. Победитель Борда - это B. Однако Дональд Саари строит пример в двух измерениях, где подсчет Борда (но не победитель Кондорсе) правильно определяет кандидата, ближайшего к центру (как определено геометрической медианой ). [11]
Диаграмма показывает возможную конфигурацию избирателей и кандидатов, соответствующую бюллетеням, с избирателями, расположенными на окружности единичного круга. В этом случае среднее абсолютное отклонение A составляет 1,15, тогда как B — 1,09 (а C — 1,70), что делает B пространственным победителем.
Таким образом, выборы неоднозначны в том смысле, что два разных пространственных представления подразумевают двух разных оптимальных победителей. Это неоднозначность, которую мы пытались избежать ранее, приняв срединную метрику для пространственных моделей; но хотя срединная метрика достигает своей цели в одном измерении, свойство не полностью обобщается на более высокие измерения.
Несмотря на этот результат, теорема о медианном избирателе может быть применена к распределениям, которые являются вращательно-симметричными, например, гауссовским , которые имеют одну медиану, которая одинакова во всех направлениях. Всякий раз, когда распределение избирателей имеет уникальную медиану во всех направлениях, и избиратели ранжируют кандидатов в порядке близости, теорема о медианном избирателе применяется: кандидат, ближайший к медиане, будет иметь большинство голосов по сравнению со всеми своими соперниками и будет избран любым методом голосования, удовлетворяющим свойству медианного избирателя в одном измерении. [12]
Отсюда следует, что все методы медианного голосования удовлетворяют одному и тому же свойству в пространствах любой размерности для распределений избирателей с ненаправленными медианами.
Легко построить распределения избирателей, которые не имеют медианы во всех направлениях. Простейший пример состоит из распределения, ограниченного 3 точками, не лежащими на прямой линии, такими как 1, 2 и 3 на второй диаграмме. Каждое местоположение избирателя совпадает с медианой при определенном наборе одномерных проекций. Если кандидатами являются A, B и C, то «1» проголосует за ABC, «2» проголосует за BCA, а «3» проголосует за CAB, что дает цикл Кондорсе. Это предмет теоремы Маккелви–Шофилда .
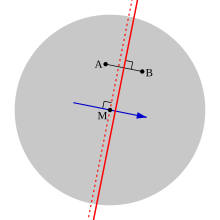
Доказательство . Смотрите диаграмму, на которой серый диск представляет распределение избирателей как равномерное по окружности, а M — медиана во всех направлениях. Пусть A и B — два кандидата, из которых A ближе к медиане. Тогда избиратели, которые ставят A выше B, — это как раз те, кто находится слева (т. е. сторона «A») от сплошной красной линии; и поскольку A ближе, чем B, к M, медиана также находится слева от этой линии.

Теперь, поскольку M является медианой во всех направлениях, она совпадает с одномерной медианой в частном случае направления, показанного синей стрелкой, которая перпендикулярна сплошной красной линии. Таким образом, если мы проведем через M ломаную красную линию, перпендикулярную синей стрелке, то мы можем сказать, что половина избирателей находится слева от этой линии. Но поскольку эта линия сама находится слева от сплошной красной линии, то из этого следует, что более половины избирателей поставят A выше B.
Всякий раз, когда существует уникальная всенаправленная медиана, она определяет результат методов голосования Кондорсе. В то же время геометрическую медиану можно, пожалуй, определить как идеального победителя выборов по ранжированным предпочтениям. Поэтому важно знать взаимосвязь между ними. Фактически, всякий раз, когда существует медиана во всех направлениях (по крайней мере, для случая дискретных распределений), она совпадает с геометрической медианой.

Лемма . Всякий раз, когда дискретное распределение имеет медиану M во всех направлениях, точки данных, не расположенные в M, должны располагаться в сбалансированных парах ( A , A ') по обе стороны от M со свойством, что A – M – A ' является прямой линией (т. е. не такой , как A0 – M – A2 на диаграмме).
Доказательство . Этот результат был алгебраически доказан Чарльзом Плоттом в 1967 году. [13] Здесь мы приводим простое геометрическое доказательство от противного в двух измерениях.
Предположим, напротив, что существует множество точек A i , которые имеют M в качестве медианы во всех направлениях, но для которых точки, не совпадающие с M , не входят в сбалансированные пары. Тогда мы можем удалить из этого множества любые точки в M , и любые сбалансированные пары около M , без того, чтобы M перестала быть медианой в любом направлении; так что M останется всенаправленной медианой.
Если число оставшихся точек нечетно, то мы можем легко провести прямую через M так , чтобы большинство точек лежало по одну сторону от нее, что противоречит свойству медианы M.
Если число четное, скажем, 2 n , то мы можем обозначить точки A 0 , A 1 ,... по часовой стрелке вокруг M, начиная с любой точки (см. диаграмму). Пусть θ будет углом, образуемым дугой от M – A 0 до M – A n . Тогда, если θ < 180°, как показано, мы можем провести линию, похожую на ломаную красную линию через M , которая имеет большинство точек данных на одной стороне, что снова противоречит свойству медианы M ; тогда как если θ > 180°, то же самое применимо к большинству точек на другой стороне. А если θ = 180°, то A 0 и A n образуют сбалансированную пару, что противоречит другому предположению.
Теорема . Всякий раз, когда дискретное распределение имеет медиану M во всех направлениях, она совпадает с его геометрической медианой.
Доказательство . Сумма расстояний от любой точки P до набора точек данных в сбалансированных парах ( A , A ' ) является суммой длин A – P – A '. Каждая отдельная длина этой формы минимизируется по P , когда линия прямая, как это происходит, когда P совпадает с M . Сумма расстояний от P до любых точек данных, расположенных в M , также минимизируется, когда P и M совпадают. Таким образом, сумма расстояний от точек данных до P минимизируется, когда P совпадает с M .
Связанное с этим наблюдение обсуждалось Гарольдом Хотеллингом как его «принцип минимальной дифференциации», также известный как « закон Хотеллинга ». Он гласит, что если:
Тогда все политики будут сходиться к медианному избирателю. В качестве особого случая этот закон применяется к ситуации, когда в гонке участвуют ровно два кандидата, если невозможно или маловероятно, что в гонку вступят еще какие-либо кандидаты, поскольку простое большинство голосов между двумя альтернативами удовлетворяет критерию Кондорсе .
Эта теорема была впервые описана Хотеллингом в 1929 году. [4] На практике ни одно из этих условий не выполняется для современных американских выборов, хотя они могли выполняться во времена Хотеллинга (когда кандидаты были публично неизвестными кандидатами, выбранными закрытыми партийными собраниями в идеологически разнообразных партиях). Самое главное, политики должны победить на первичных выборах , которые часто включают претендентов или конкурентов, чтобы быть выбранными в качестве кандидатов от основных партий. В результате политики должны идти на компромисс между обращением к среднему избирателю в первичном и общем электорате. Аналогичные эффекты подразумевают, что кандидаты не сходятся к среднему избирателю в избирательных системах , которые не удовлетворяют теореме о медианном избирателе, включая большинство голосов , большинство голосов с праймериз , большинство голосов с последним туром или ранжированный последний тур (RCV) . [5] [14]
Теорема ценна тем, что проливает свет на оптимальность (и пределы оптимальности) некоторых систем голосования.
Валерио Дотти указывает на более широкие области применения:
Теорема о медианном избирателе оказалась чрезвычайно популярной в литературе по политической экономии. Основная причина в том, что ее можно использовать для получения проверяемых выводов о связи между некоторыми характеристиками голосующего населения и результатами политики, абстрагируясь от других особенностей политического процесса. [12]
Он добавляет, что...
Медианный результат голосования применялся к невероятному количеству вопросов. Примерами являются анализ взаимосвязи между неравенством доходов и размером государственного вмешательства в политику перераспределения (Meltzer and Richard, 1981), [15] исследование детерминант иммиграционной политики (Razin and Sadka, 1999), [16] масштабов налогообложения различных видов доходов (Bassetto and Benhabib, 2006), [17] и многое другое.