В криптографии блочный шифр — это детерминированный алгоритм , который работает с группами битов фиксированной длины , называемыми блоками . Блочные шифры — это элементарные строительные блоки многих криптографических протоколов . Они повсеместно используются при хранении и обмене данными, где такие данные защищены и аутентифицированы с помощью шифрования .
Блочный шифр использует блоки как неизменяемое преобразование. Даже безопасный блочный шифр подходит для шифрования только одного блока данных за раз с использованием фиксированного ключа. Было разработано множество режимов работы , чтобы обеспечить их повторное использование безопасным способом для достижения целей безопасности конфиденциальности и подлинности . Однако блочные шифры могут также выступать в качестве строительных блоков в других криптографических протоколах, таких как универсальные хэш-функции и генераторы псевдослучайных чисел .

Блочный шифр состоит из двух парных алгоритмов , один для шифрования, E , и другой для расшифровки, D . [1] Оба алгоритма принимают два входа: входной блок размером n бит и ключ размером k бит; и оба выдают n -битный выходной блок. Алгоритм расшифровки D определяется как обратная функция шифрования, т. е. D = E −1 . Более формально, [2] [3] блочный шифр задается функцией шифрования
которая принимает в качестве входных данных ключ K длиной k бит ( называемый размером ключа ) и строку бит P длиной n (называемый размером блока ) и возвращает строку C длиной n бит. P называется открытым текстом , а C называется зашифрованным текстом . Для каждого K функция E K ( P ) должна быть обратимым отображением на {0,1} n . Обратная функция для E определяется как функция
принимая ключ K и зашифрованный текст C, чтобы вернуть значение открытого текста P , такое, что
Например, алгоритм шифрования блочного шифра может принимать 128-битный блок открытого текста в качестве входных данных и выводить соответствующий 128-битный блок зашифрованного текста. Точное преобразование контролируется с помощью второго входа – секретного ключа. Расшифровка аналогична: алгоритм расшифровки принимает, в этом примере, 128-битный блок зашифрованного текста вместе с секретным ключом и выдает исходный 128-битный блок открытого текста. [4]
Для каждого ключа K , E K является перестановкой ( биективным отображением) над набором входных блоков. Каждый ключ выбирает одну перестановку из набора возможных перестановок. [5]
Современная конструкция блочных шифров основана на концепции итеративного шифра произведения . В своей основополагающей публикации 1949 года «Теория связи в секретных системах » Клод Шеннон проанализировал шифры произведения и предложил их в качестве средства эффективного повышения безопасности путем объединения простых операций, таких как подстановки и перестановки . [6] Итеративно-произведенные шифры выполняют шифрование в несколько раундов , каждый из которых использует другой подключ, полученный из исходного ключа. Одна из широко распространенных реализаций таких шифров, названная сетью Фейстеля в честь Хорста Фейстеля , в частности, реализована в шифре DES . [7] Многие другие реализации блочных шифров, такие как AES , классифицируются как сети подстановки-перестановки . [8]
Корень всех криптографических форматов блоков, используемых в стандарте безопасности данных индустрии платежных карт (PCI DSS) и стандартах Американского национального института стандартов (ANSI), лежит в Atalla Key Block (AKB), который был ключевым нововведением Atalla Box , первого аппаратного модуля безопасности (HSM). Он был разработан в 1972 году Мохамедом М. Аталлой , основателем Atalla Corporation (теперь Utimaco Atalla ), и выпущен в 1973 году. AKB был ключевым блоком, который требовался для безопасного обмена симметричными ключами или PIN-кодами с другими участниками банковской отрасли . Этот безопасный обмен выполняется с использованием формата AKB. [9] Atalla Box защищал более 90% всех сетей банкоматов , находящихся в эксплуатации по состоянию на 1998 год, [10] и продукты Atalla по-прежнему защищают большинство транзакций банкоматов в мире по состоянию на 2014 год. [11]
Публикация шифра DES Национальным бюро стандартов США (впоследствии Национальным институтом стандартов и технологий США , NIST) в 1977 году имела основополагающее значение для общественного понимания современного дизайна блочных шифров. Она также повлияла на академическое развитие криптоаналитических атак . Как дифференциальный , так и линейный криптоанализ возникли из исследований дизайна DES. По состоянию на 2016 год [обновлять]существует палитра методов атак, против которых блочный шифр должен быть защищен, в дополнение к тому, чтобы быть устойчивым к атакам методом перебора .
Большинство алгоритмов блочного шифрования классифицируются как итеративные блочные шифры , что означает, что они преобразуют блоки фиксированного размера открытого текста в блоки идентичного размера зашифрованного текста посредством многократного применения обратимого преобразования, известного как функция раунда , при этом каждая итерация называется раундом . [ 12]
Обычно функция раунда R принимает различные ключи раунда K i в качестве второго входа, который выводится из исходного ключа: [13]
где — открытый текст и зашифрованный текст, где r — количество раундов.
Часто в дополнение к этому используется отбеливание ключа . В начале и в конце данные модифицируются ключевым материалом (часто с помощью XOR ):
Учитывая одну из стандартных схем проектирования итерационного блочного шифра, довольно легко построить блочный шифр, который будет криптографически безопасен, просто используя большое количество раундов. Однако это сделает шифр неэффективным. Таким образом, эффективность является наиболее важным дополнительным критерием проектирования для профессиональных шифров. Кроме того, хороший блочный шифр разработан так, чтобы избегать атак по побочным каналам, таких как предсказание ветвлений и доступ к памяти, зависящий от ввода, которые могут привести к утечке секретных данных через состояние кэша или время выполнения. Кроме того, шифр должен быть кратким для небольших аппаратных и программных реализаций.

Один важный тип итерационного блочного шифра, известный как сеть подстановки-перестановки (SPN), берет блок открытого текста и ключ в качестве входных данных и применяет несколько чередующихся раундов, состоящих из этапа подстановки, за которым следует этап перестановки , — для получения каждого блока выходного шифртекста. [14] Нелинейный этап подстановки смешивает биты ключа с битами открытого текста, создавая путаницу Шеннона . Затем линейный этап перестановки рассеивает избыточность, создавая диффузию . [15] [16]
Подстановочный блок ( S-box) заменяет небольшой блок входных бит другим блоком выходных бит. Эта подстановка должна быть один к одному , чтобы обеспечить обратимость (следовательно, расшифровку). Защищенный S-box будет обладать свойством, что изменение одного входного бита изменит в среднем около половины выходных битов, демонстрируя то, что известно как эффект лавины — т. е. он обладает свойством, что каждый выходной бит будет зависеть от каждого входного бита. [17]
Ящик перестановки (P-ящик) — это перестановка всех битов: он берет выходы всех S-ящиков одного раунда, переставляет биты и подает их в S-ящики следующего раунда. Хороший P-ящик обладает тем свойством, что выходные биты любого S-ящика распределяются по максимально возможному количеству входов S-ящиков. [ необходима цитата ]
На каждом раунде ключ раунда (полученный из ключа с помощью некоторых простых операций, например, с использованием S-блоков и P-блоков) объединяется с помощью некоторой групповой операции, обычно XOR . [ необходима цитата ]
Расшифровка выполняется простым обратным процессом (используя инверсии S-блоков и P-блоков и применяя раундовые ключи в обратном порядке). [18]
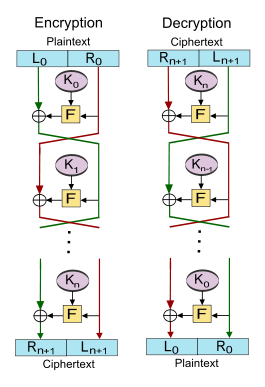
В шифре Фейстеля блок открытого текста, который нужно зашифровать, делится на две равные по размеру половины. Функция раунда применяется к одной половине с использованием подключа, а затем выходной сигнал подвергается операции XOR с другой половиной. Затем две половины меняются местами. [19]
Пусть будет функцией раунда, а пусть будут подключи для раундов соответственно.
Тогда основная операция выглядит следующим образом: [19]
Разделить блок открытого текста на две равные части, ( , )
Для каждого раунда вычислите
Тогда шифртекст будет таким .
Расшифровка зашифрованного текста выполняется путем вычисления
И снова открытый текст.
Одним из преимуществ модели Фейстеля по сравнению с сетью подстановки-перестановки является то, что раундовая функция не обязательно должна быть обратимой. [20]
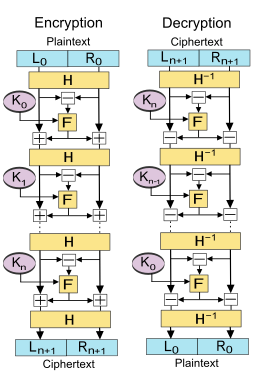
Схема Лая–Месси предлагает свойства безопасности, аналогичные свойствам структуры Фейстеля . Она также разделяет преимущество, заключающееся в том, что функция раунда не обязательно должна быть обратимой. Другое сходство заключается в том, что она также разделяет входной блок на две равные части. Однако функция раунда применяется к разнице между ними, а затем результат добавляется к обоим полублокам.
Пусть — функция раунда и функция полураунда, а — подключи для раундов соответственно.
Тогда основная операция будет следующей:
Разделить блок открытого текста на две равные части, ( , )
Для каждого раунда вычислите
где и
Тогда шифртекст будет таким .
Расшифровка зашифрованного текста выполняется путем вычисления
где и
И снова открытый текст.
Многие современные блочные шифры и хэши являются алгоритмами ARX — их раундовая функция включает всего три операции: (A) модульное сложение, (R) поворот с фиксированными величинами поворота и (X) XOR . Примерами являются ChaCha20 , Speck , XXTEA и BLAKE . Многие авторы рисуют сеть ARX, своего рода диаграмму потока данных , чтобы проиллюстрировать такую раундовую функцию. [21]
Эти операции ARX популярны, потому что они относительно быстры и дешевы в аппаратном и программном обеспечении, их реализация может быть сделана чрезвычайно простой, а также потому, что они работают за постоянное время и, следовательно, невосприимчивы к атакам по времени . Метод ротационного криптоанализа пытается атаковать такие раундовые функции.
Другие операции, часто используемые в блочных шифрах, включают в себя зависящие от данных вращения, как в RC5 и RC6 , блок подстановки, реализованный в виде таблицы поиска , как в Data Encryption Standard и Advanced Encryption Standard , блок перестановки и умножение, как в IDEA .
Блочный шифр сам по себе позволяет шифровать только один блок данных длины блока шифра. Для сообщения переменной длины данные должны быть сначала разделены на отдельные блоки шифра. В простейшем случае, известном как режим электронной кодовой книги (ECB), сообщение сначала разбивается на отдельные блоки размера блока шифра (возможно, расширяя последний блок битами заполнения ), а затем каждый блок шифруется и расшифровывается независимо. Однако такой наивный метод, как правило, небезопасен, поскольку равные блоки открытого текста всегда будут генерировать равные блоки зашифрованного текста (для одного и того же ключа), поэтому шаблоны в сообщении открытого текста становятся очевидными в выходном зашифрованном тексте. [22]
Чтобы преодолеть это ограничение, было разработано несколько так называемых режимов работы блочного шифра [23] [24] и указано в национальных рекомендациях, таких как NIST 800-38A [25] и BSI TR-02102 [26] , и международных стандартах, таких как ISO/IEC 10116. [ 27] Общая концепция заключается в использовании рандомизации данных открытого текста на основе дополнительного входного значения, часто называемого вектором инициализации , для создания того, что называется вероятностным шифрованием . [28] В популярном режиме цепочки блоков шифра (CBC) для обеспечения безопасности шифрования вектор инициализации, передаваемый вместе с сообщением открытого текста, должен быть случайным или псевдослучайным значением, которое добавляется в порядке исключающего ИЛИ к первому блоку открытого текста перед его шифрованием. Полученный блок шифртекста затем используется в качестве нового вектора инициализации для следующего блока открытого текста. В режиме обратной связи шифра (CFB), который эмулирует самосинхронизирующийся потоковый шифр , вектор инициализации сначала шифруется, а затем добавляется к блоку открытого текста. Режим обратной связи выхода (OFB) многократно шифрует вектор инициализации для создания ключевого потока для эмуляции синхронного потокового шифра . Более новый режим счетчика (CTR) аналогичным образом создает ключевой поток, но имеет преимущество в том, что в качестве векторов инициализации требуются только уникальные, а не (псевдо)случайные значения; необходимая случайность получается внутренне путем использования вектора инициализации в качестве счетчика блоков и шифрования этого счетчика для каждого блока. [25]
С точки зрения теории безопасности режимы работы должны обеспечивать то, что известно как семантическая безопасность . [29] Неформально это означает, что, имея некоторый шифртекст под неизвестным ключом, невозможно практически извлечь какую-либо информацию из шифртекста (кроме длины сообщения) сверх того, что можно было бы узнать, не видя шифртекста. Было показано, что все режимы, обсуждавшиеся выше, за исключением режима ECB, обеспечивают это свойство при так называемых атаках с выбранным открытым текстом .
Некоторые режимы, такие как режим CBC, работают только с полными блоками открытого текста. Простого расширения последнего блока сообщения нулевыми битами недостаточно, поскольку это не позволяет получателю легко различать сообщения, которые отличаются только количеством битов заполнения. Что еще более важно, такое простое решение приводит к очень эффективным атакам оракула заполнения . [30] Поэтому необходима подходящая схема заполнения , чтобы расширить последний блок открытого текста до размера блока шифра. В то время как многие популярные схемы, описанные в стандартах и в литературе, как было показано, уязвимы для атак оракула заполнения, [30] [31] решение, которое добавляет один бит, а затем расширяет последний блок нулевыми битами, стандартизированное как «метод заполнения 2» в ISO/IEC 9797-1, [32] было доказано безопасным против этих атак. [31]
Это свойство приводит к квадратичному снижению безопасности шифра и должно учитываться при выборе размера блока. Однако существует компромисс, поскольку большие размеры блоков могут привести к тому, что алгоритм станет неэффективным в работе. [33] Более ранние блочные шифры, такие как DES, обычно выбирали 64-битный размер блока, в то время как более новые разработки, такие как AES, поддерживают размеры блоков 128 бит и более, а некоторые шифры поддерживают ряд различных размеров блоков. [34]
Линейный криптоанализ — это форма криптоанализа, основанная на поиске аффинных приближений к действию шифра . Линейный криптоанализ — одна из двух наиболее широко используемых атак на блочные шифры; другая — дифференциальный криптоанализ . [35]
Открытие приписывается Мицуру Мацуи , который первым применил эту технику к шифру FEAL (Мацуи и Ямагиши, 1992). [36]
Интегральный криптоанализ — это криптоаналитическая атака, которая особенно применима к блочным шифрам, основанным на сетях подстановки-перестановки. В отличие от дифференциального криптоанализа, который использует пары выбранных открытых текстов с фиксированной разницей XOR, интегральный криптоанализ использует наборы или даже мультинаборы выбранных открытых текстов, часть из которых сохраняется постоянной, а другая часть варьируется во всех возможных вариантах. Например, атака может использовать 256 выбранных открытых текстов, у которых все, кроме 8 битов, одинаковы, но все отличаются этими 8 битами. Такой набор обязательно имеет сумму XOR равную 0, а суммы XOR соответствующих наборов шифртекстов предоставляют информацию о работе шифра. Этот контраст между различиями между парами текстов и суммами более крупных наборов текстов вдохновил на название «интегральный криптоанализ», заимствовав терминологию исчисления. [ необходима цитата ]

В дополнение к линейному и дифференциальному криптоанализу, существует растущий каталог атак: усеченный дифференциальный криптоанализ , частичный дифференциальный криптоанализ, интегральный криптоанализ , который охватывает квадратные и интегральные атаки, скользящие атаки , атаки бумеранга , атаку XSL , невозможный дифференциальный криптоанализ и алгебраические атаки. Для того, чтобы новый дизайн блочного шифра имел какое-либо доверие, он должен продемонстрировать доказательства безопасности против известных атак. [ необходима цитата ]
Когда блочный шифр используется в заданном режиме работы , результирующий алгоритм в идеале должен быть примерно таким же безопасным, как и сам блочный шифр. ECB (обсуждавшийся выше) решительно лишен этого свойства: независимо от того, насколько безопасен базовый блочный шифр, режим ECB может быть легко атакован. С другой стороны, можно доказать безопасность режима CBC, предположив, что базовый блочный шифр также безопасен. Обратите внимание, однако, что для подобных утверждений требуются формальные математические определения того, что означает для алгоритма шифрования или блочного шифра «быть безопасным». В этом разделе описываются два общих понятия о том, какими свойствами должен обладать блочный шифр. Каждое из них соответствует математической модели, которая может использоваться для доказательства свойств алгоритмов более высокого уровня, таких как CBC.
Этот общий подход к криптографии — доказательство безопасности алгоритмов более высокого уровня (таких как CBC) при явно сформулированных предположениях относительно их компонентов (таких как блочный шифр) — известен как доказуемая безопасность .
Неформально, блочный шифр является безопасным в стандартной модели, если злоумышленник не может отличить блочный шифр (оснащенный случайным ключом) от случайной перестановки.
Чтобы быть немного точнее, пусть E будет n -битным блочным шифром. Представим себе следующую игру:
Атакующий, которого мы можем смоделировать как алгоритм, называется противником . Функция f (которую противник смог запросить) называется оракулом .
Обратите внимание, что противник может тривиально гарантировать 50% шансов на победу, просто угадывая наугад (или даже, например, всегда угадывая «орел»). Поэтому пусть P E ( A ) обозначает вероятность того, что противник A выиграет эту игру против E , и определит преимущество A как 2( P E ( A ) − 1/2). Из этого следует, что если A угадывает случайно, его преимущество будет равно 0; с другой стороны, если A всегда выигрывает, то его преимущество равно 1. Блочный шифр E является псевдослучайной перестановкой (PRP), если ни один противник не имеет преимущества, значительно большего 0, учитывая заданные ограничения на q и время выполнения противника. Если на шаге 2 выше у противников есть возможность изучить f −1 ( X ) вместо f ( X ) (но все еще имеют только небольшие преимущества), то E является сильным PRP (SPRP). Противник неадаптивен, если он выбирает все значения q для X до начала игры (то есть он не использует никакую информацию, полученную из предыдущих запросов, для выбора каждого X по ходу игры).
Эти определения оказались полезными для анализа различных режимов работы. Например, можно определить похожую игру для измерения безопасности алгоритма шифрования на основе блочного шифра, а затем попытаться показать (с помощью аргумента сокращения ), что вероятность победы противника в этой новой игре не намного больше, чем P E ( A ) для некоторого A . (Сокращение обычно обеспечивает ограничения на q и время выполнения A .) Эквивалентно, если P E ( A ) мало для всех соответствующих A , то ни один злоумышленник не имеет значительной вероятности выиграть новую игру. Это формализует идею о том, что алгоритм более высокого уровня наследует безопасность блочного шифра.
Блочные шифры могут быть оценены по нескольким критериям на практике. Общие факторы включают: [37] [38]
Lucifer обычно считается первым гражданским блочным шифром, разработанным в IBM в 1970-х годах на основе работы, проделанной Хорстом Фейстелем . Пересмотренная версия алгоритма была принята в качестве федерального стандарта обработки информации правительства США : FIPS PUB 46 Data Encryption Standard (DES). [40] Он был выбран Национальным бюро стандартов США (NBS) после публичного приглашения к представлению и некоторых внутренних изменений со стороны NBS (и, возможно, NSA ). DES был публично выпущен в 1976 году и широко использовался. [ необходима цитата ]
DES был разработан, среди прочего, для сопротивления определенной криптоаналитической атаке, известной АНБ и заново открытой IBM, хотя и неизвестной публично, пока она не была заново открыта и опубликована Эли Бихамом и Ади Шамиром в конце 1980-х годов. Эта техника называется дифференциальным криптоанализом и остается одной из немногих общих атак против блочных шифров; линейный криптоанализ является еще одной, но, возможно, был неизвестен даже АНБ до ее публикации Мицуру Мацуи . DES побудил большое количество других работ и публикаций по криптографии и криптоанализу в открытом сообществе и вдохновил на создание многих новых конструкций шифров. [ необходима цитата ]
DES имеет размер блока 64 бита и размер ключа 56 бит. 64-битные блоки стали обычным явлением в конструкциях блочных шифров после DES. Длина ключа зависела от нескольких факторов, включая государственное регулирование. Многие наблюдатели [ кто? ] в 1970-х годах отмечали, что длина 56-битного ключа, используемая для DES, была слишком короткой. Со временем его неадекватность стала очевидной, особенно после того, как в 1998 году Electronic Frontier Foundation продемонстрировала специальную машину, предназначенную для взлома DES . Расширение DES, Triple DES , тройное шифрование каждого блока либо двумя независимыми ключами (112-битный ключ и 80-битная безопасность), либо тремя независимыми ключами (168-битный ключ и 112-битная безопасность). Он был широко принят в качестве замены. По состоянию на 2011 год версия с тремя ключами по-прежнему считается безопасной, хотя стандарты Национального института стандартов и технологий (NIST) больше не разрешают использование версии с двумя ключами в новых приложениях из-за ее 80-битного уровня безопасности. [41]
Международный алгоритм шифрования данных ( IDEA ) — это блочный шифр, разработанный Джеймсом Мэсси из Швейцарской высшей технической школы Цюриха и Сюэцзя Лаем ; он был впервые описан в 1991 году как предполагаемая замена DES.
IDEA работает с 64-битными блоками, используя 128-битный ключ, и состоит из серии из восьми идентичных преобразований ( раунд ) и выходного преобразования (полураунд ) . Процессы шифрования и дешифрования схожи. IDEA получает большую часть своей безопасности путем чередования операций из разных групп — модульного сложения и умножения, а также побитового исключающего или (XOR) — которые алгебраически «несовместимы» в некотором смысле.
Разработчики проанализировали IDEA, чтобы измерить его силу против дифференциального криптоанализа , и пришли к выводу, что он неуязвим при определенных предположениях. Не было зарегистрировано ни одной успешной линейной[update] или алгебраической уязвимости. По состоянию на 2012 год лучшая атака, которая применима ко всем ключам, может взломать полную 8,5-раундовую IDEA с использованием атаки узкими бикликами примерно в четыре раза быстрее, чем методом грубой силы.

RC5 — это блочный шифр, разработанный Рональдом Ривестом в 1994 году, который, в отличие от многих других шифров, имеет переменный размер блока (32, 64 или 128 бит), размер ключа (от 0 до 2040 бит) и количество раундов (от 0 до 255). Первоначально предложенный выбор параметров был следующим: размер блока 64 бита, 128-битный ключ и 12 раундов.
Ключевой особенностью RC5 является использование зависящих от данных ротаций; одной из целей RC5 было побудить к изучению и оценке таких операций как криптографического примитива. RC5 также состоит из ряда модульных сложений и XOR. Общая структура алгоритма представляет собой сеть типа Фейстеля . Процедуры шифрования и дешифрования могут быть указаны в нескольких строках кода. Однако ключевой график более сложен, расширяя ключ с использованием по существу односторонней функции с двоичными расширениями как e, так и золотого сечения в качестве источников « ничего в моем рукаве ». Заманчивая простота алгоритма вместе с новизной зависящих от данных ротаций сделали RC5 привлекательным объектом изучения для криптоаналитиков.
12-раундовый RC5 (с 64-битными блоками) уязвим для дифференциальной атаки с использованием 244 выбранных открытых текстов. [42] В качестве достаточной защиты предлагается 18–20 раундов.
Шифр Rijndael , разработанный бельгийскими криптографами Джоаном Даеменом и Винсентом Рейменом, был одним из конкурирующих проектов по замене DES. Он выиграл 5-летний публичный конкурс на звание AES (Advanced Encryption Standard).
Принятый NIST в 2001 году, AES имеет фиксированный размер блока 128 бит и размер ключа 128, 192 или 256 бит, тогда как Rijndael может быть указан с размерами блока и ключа в любом кратном 32 битам, с минимальным значением 128 бит. Размер блока имеет максимум 256 бит, но размер ключа не имеет теоретического максимума. AES работает на матрице байтов 4×4 в столбцовом порядке , называемой состоянием (версии Rijndael с большим размером блока имеют дополнительные столбцы в состоянии).
Blowfish — это блочный шифр, разработанный в 1993 году Брюсом Шнайером и включенный в большое количество наборов шифров и продуктов шифрования. Blowfish имеет 64-битный размер блока и переменную длину ключа от 1 до 448 бит. [43] Это 16-раундовый шифр Фейстеля , использующий большие зависимые от ключа S-блоки . Известные особенности дизайна включают зависимые от ключа S-блоки и очень сложное расписание ключей .
Он был разработан как алгоритм общего назначения, предназначенный в качестве альтернативы устаревшему DES и свободный от проблем и ограничений, связанных с другими алгоритмами. На момент выпуска Blowfish многие другие разработки были запатентованы, обременены патентами или были коммерческими/правительственными секретами. Шнайер заявил, что «Blowfish не запатентован и останется таковым во всех странах. Настоящим алгоритм помещается в общественное достояние и может свободно использоваться любым человеком». То же самое относится к Twofish , алгоритму-преемнику от Шнайера.
M. Liskov, R. Rivest и D. Wagner описали обобщенную версию блочных шифров, называемых «настраиваемыми» блочными шифрами. [44] Настраиваемый блочный шифр принимает второй вход, называемый твиком, вместе с его обычным открытым текстом или зашифрованным текстом. Твик вместе с ключом выбирает перестановку, вычисленную шифром. Если изменение твиков достаточно легкое (по сравнению с обычно довольно дорогой операцией по установке ключа), то становятся возможными некоторые интересные новые режимы работы. Статья о теории шифрования дисков описывает некоторые из этих режимов.
Блочные шифры традиционно работают с двоичным алфавитом . То есть, и вход, и выход являются двоичными строками, состоящими из n нулей и единиц. Однако в некоторых ситуациях может потребоваться блочный шифр, работающий с каким-либо другим алфавитом; например, шифрование 16-значных номеров кредитных карт таким образом, чтобы шифртекст также был 16-значным числом, может облегчить добавление слоя шифрования в устаревшее программное обеспечение. Это пример шифрования с сохранением формата . В более общем смысле, шифрование с сохранением формата требует ключевой перестановки на некотором конечном языке . Это делает схемы шифрования с сохранением формата естественным обобщением (настраиваемых) блочных шифров. Напротив, традиционные схемы шифрования, такие как CBC, не являются перестановками, поскольку один и тот же открытый текст может шифровать несколько различных шифртекстов, даже при использовании фиксированного ключа.
Блочные шифры могут использоваться для построения других криптографических примитивов, таких как те, что приведены ниже. Чтобы эти другие примитивы были криптографически безопасными, необходимо позаботиться о том, чтобы построить их правильным способом.
Так же, как блочные шифры могут использоваться для построения хэш-функций, как SHA-1 и SHA-2, основанные на блочных шифрах, которые также используются независимо как SHACAL , хэш-функции могут использоваться для построения блочных шифров. Примерами таких блочных шифров являются BEAR и LION .
{{cite journal}}: Цитировать журнал требует |journal=( помощь )