Алгоритм, игнорирующий кэш

В вычислительной технике алгоритм, игнорирующий кэш ( или трансцендентный кэшу алгоритм) — это алгоритм , разработанный для использования кэша процессора без явного указания размера кэша (или длины строк кэша и т. д.). Оптимальный алгоритм , игнорирующий кэш, — это алгоритм, игнорирующий кэш, который использует кэш оптимально (в асимптотическом смысле, игнорируя постоянные факторы). Таким образом, алгоритм, игнорирующий кэш, разработан для хорошей работы без изменений на нескольких машинах с разными размерами кэша или для иерархии памяти с разными уровнями кэша, имеющими разные размеры. Алгоритмы, игнорирующие кэш, противопоставляются явному тайлингу цикла , который явно разбивает задачу на блоки, которые имеют оптимальный размер для заданного кэша.

Оптимальные алгоритмы, забывающие о кэше, известны для умножения матриц , транспонирования матриц , сортировки и ряда других задач. Некоторые более общие алгоритмы, такие как Кули–Тьюки FFT , являются оптимально забывающими о кэше при определенном выборе параметров. Поскольку эти алгоритмы оптимальны только в асимптотическом смысле (игнорируя постоянные множители), может потребоваться дополнительная машинно-специфическая настройка для получения почти оптимальной производительности в абсолютном смысле. Целью алгоритмов, забывающих о кэше, является уменьшение объема такой необходимой настройки.

Обычно алгоритм, игнорирующий кэш, работает по рекурсивному алгоритму «разделяй и властвуй» , где проблема делится на все меньшие и меньшие подзадачи. В конце концов, достигается размер подзадачи, который помещается в кэш, независимо от размера кэша. Например, оптимальное умножение матриц, игнорирующее кэш, получается путем рекурсивного деления каждой матрицы на четыре подматрицы для умножения, умножая подматрицы в глубину . [ ^{необходима цитата ]} При настройке для конкретной машины можно использовать гибридный алгоритм , который использует циклическую мозаику, настроенную для определенных размеров кэша на нижнем уровне, но в противном случае использует алгоритм, игнорирующий кэш.

История

Идея (и название) алгоритмов, забывающих о кэше, была задумана Чарльзом Э. Лейзерсоном еще в 1996 году и впервые опубликована Харальдом Прокопом в его магистерской диссертации в Массачусетском технологическом институте в 1999 году. ^[1] Было много предшественников, обычно анализировавших конкретные проблемы; они подробно обсуждаются в работе Фриго и др. 1999 года. Среди ранних приведенных примеров можно назвать Синглтона 1969 года для рекурсивного быстрого преобразования Фурье, похожие идеи в работе Аггарвала и др. 1987 года, Фриго 1996 года для умножения матриц и LU-разложения и Тодда Вельдхёйзена 1996 года для матричных алгоритмов в библиотеке Blitz++ .

Идеализированная модель кэша

В общем случае программу можно сделать более сознательной в отношении кэша: ^[2]

Временная локальность , когда алгоритм извлекает одни и те же фрагменты памяти несколько раз;
Пространственная локальность , где последующие обращения к памяти осуществляются по соседним или близлежащим адресам памяти .

Алгоритмы, забывающие о кэше, обычно анализируются с использованием идеализированной модели кэша, иногда называемой моделью, забывающей о кэше . Эту модель гораздо проще анализировать, чем характеристики реального кэша (которые имеют сложную ассоциативность, политики замены и т. д.), но во многих случаях она, как доказуемо, находится в пределах постоянного множителя более реалистичной производительности кэша. Она отличается от модели внешней памяти , поскольку алгоритмы, забывающие о кэше, не знают размер блока или размер кэша .

В частности, модель с кэш-забвением является абстрактной машиной (т. е. теоретической моделью вычислений ). Она похожа на модель машины с ОЗУ , которая заменяет бесконечную ленту машины Тьюринга бесконечным массивом. К каждому месту в массиве можно получить доступ со временем, аналогично памяти с произвольным доступом на реальном компьютере. В отличие от модели машины с ОЗУ, она также вводит кэш: второй уровень хранения между ОЗУ и ЦП. Другие различия между двумя моделями перечислены ниже. В модели с кэш-забвением: $O(1)$

Память разбита на блоки объектов каждый. $Б$
Загрузка или сохранение между основной памятью и регистром ЦП теперь может выполняться из кэша.
Если загрузка или сохранение не могут быть выполнены из кэша, это называется промахом кэша .
Промах кэша приводит к загрузке одного блока из основной памяти в кэш. А именно, если ЦП пытается получить доступ к слову и является строкой, содержащей , то загружается в кэш. Если кэш был ранее заполнен, то строка также будет вытеснена (см. политику замены ниже). $w$ $x$ $w$ $x$
Кэш содержит объекты, где . Это также известно как предположение о высоком кэше . $М$ $М=\Омега (B^{2})$
Кэш полностью ассоциативен: каждая строка может быть загружена в любое место кэша. ^[3]
Политика замены является оптимальной. Другими словами, предполагается, что кэшу предоставлена вся последовательность обращений к памяти во время выполнения алгоритма. Если ему необходимо вытеснить строку в момент времени , он проверит последовательность своих будущих запросов и вытеснит строку, первый доступ к которой находится дальше всего в будущем. Это можно эмулировать на практике с помощью политики Least Recently Used , которая, как показано, находится в пределах небольшого постоянного множителя оптимальной стратегии замены в автономном режиме ^[4]^[5] $т$

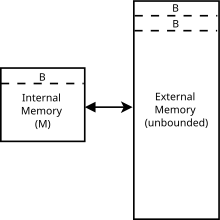
Чтобы измерить сложность алгоритма, который выполняется в модели, забывающей кэш, мы измеряем количество промахов кэша , которые испытывает алгоритм. Поскольку модель фиксирует тот факт, что доступ к элементам в кэше намного быстрее, чем доступ к вещам в основной памяти , время выполнения алгоритма определяется только количеством передач памяти между кэшем и основной памятью. Это похоже на модель внешней памяти , которая обладает всеми вышеперечисленными характеристиками, но алгоритмы, забывающие кэш, не зависят от параметров кэша ( и ). ^[6] Преимущество такого алгоритма заключается в том, что то, что эффективно на машине, забывающей кэш, вероятно, будет эффективным на многих реальных машинах без тонкой настройки для конкретных параметров реальной машины. Для многих задач оптимальный алгоритм, забывающий кэш, также будет оптимальным для машины с более чем двумя уровнями иерархии памяти . ^[4] $Б$ $М$

Примеры

Простейший алгоритм, игнорирующий кэш, представленный в работе Фриго и др., представляет собой операцию транспонирования матрицы вне ее места ( алгоритмы на месте также были разработаны для транспонирования, но они гораздо сложнее для неквадратных матриц). Учитывая массив A размером m × n и массив B размером n × m , мы хотели бы сохранить транспонирование $A$ в $B.$ Наивное решение обходит один массив в порядке по строкам, а другой — в порядке по столбцам. Результатом является то, что когда матрицы большие, мы получаем промах кэша на каждом шаге обхода по столбцам. Общее количество промахов кэша равно . $\Тета (mn)$

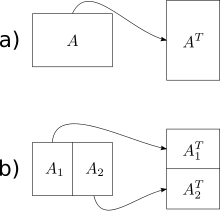
Алгоритм, игнорирующий кэш, имеет оптимальную сложность работы и оптимальную сложность кэша . Основная идея заключается в том, чтобы свести транспонирование двух больших матриц к транспонированию маленьких (под)матриц. Мы делаем это, разделяя матрицы пополам по их большему измерению, пока нам просто не нужно будет выполнить транспонирование матрицы, которая поместится в кэш. Поскольку размер кэша алгоритму неизвестен, матрицы будут продолжать делиться рекурсивно даже после этой точки, но эти дальнейшие подразделения будут находиться в кэше. Как только измерения $m$ и $n$ станут достаточно малы, чтобы входной массив размера и выходной массив размера поместились в кэш, как строковый, так и столбцовый обходы приведут к промахам работы и кэша. Используя этот подход «разделяй и властвуй», мы можем достичь того же уровня сложности для всей матрицы. $O(mn)$ $O(1+mn/B)$ $m\times n$ $n\times m$ $O(mn)$ $O(mn/B)$

(В принципе, можно было бы продолжать делить матрицы до тех пор, пока не будет достигнут базовый случай размера 1×1, но на практике используют больший базовый случай (например, 16×16), чтобы компенсировать накладные расходы на рекурсивные вызовы подпрограмм.)

Большинство алгоритмов, игнорирующих кэш, полагаются на подход «разделяй и властвуй». Они уменьшают проблему, так что она в конечном итоге помещается в кэш, независимо от того, насколько мал кэш, и заканчивают рекурсию на некотором небольшом размере, определяемом накладными расходами на вызов функции и аналогичными оптимизациями, не связанными с кэшем, а затем используют некий эффективный для кэша шаблон доступа для объединения результатов этих небольших решенных проблем.

Подобно внешней сортировке в модели внешней памяти , сортировка с учетом кэша возможна в двух вариантах: сортировка воронкой , которая напоминает сортировку слиянием ; и сортировка с учетом кэша , которая напоминает быструю сортировку . Как и их аналоги с внешней памятью, обе достигают времени выполнения , что соответствует нижней границе и, таким образом, является асимптотически оптимальным . ^[6] $O\left({\tfrac {N}{B}}\log _{\tfrac {M}{B}}{\tfrac {N}{B}}\right)$

Практичность

Эмпирическое сравнение двух алгоритмов на основе ОЗУ, одного с учетом кэша и двух алгоритмов без учета кэша, реализующих приоритетные очереди , показало, что: ^[7]

Алгоритмы, игнорирующие кэш, работали хуже, чем алгоритмы, основанные на оперативной памяти и учитывающие кэш, когда данные помещались в основную память.
Алгоритм с учетом кэша не показался значительно более сложным в реализации, чем алгоритмы без учета кэша, и продемонстрировал наилучшую производительность во всех случаях, протестированных в исследовании.
Алгоритмы, игнорирующие кэш, превосходят алгоритмы на основе оперативной памяти, когда объем данных превышает объем основной памяти.

В другом исследовании сравнивались хэш-таблицы (как основанные на RAM или не поддерживающие кэш), B-деревья (как поддерживающие кэш) и структура данных, игнорирующая кэш, называемая «набор Бендера». Как по времени выполнения, так и по использованию памяти, хэш-таблица была лучшей, за ней следовало B-дерево, а набор Бендера был наихудшим во всех случаях. Использование памяти для всех тестов не превышало основной памяти. Хэш-таблицы были описаны как простые в реализации, в то время как набор Бендера «требовал больших усилий для правильной реализации». ^[8]

Смотрите также

Ссылки

^ Харальд Прокоп. Алгоритмы, забывающие кэш. Магистерская диссертация, Массачусетский технологический институт. 1999.
^ Аскитис, Николас; Зобель, Джастин (2005). «Разрешение коллизий с использованием кэша в строковых хэш-таблицах». Международный симпозиум по обработке строк и поиску информации . Springer : 93. doi :10.1007/11575832_1. ISBN 978-3-540-29740-6.
^ Кумар, Пиюш. «Кэш-забывчивые алгоритмы». Алгоритмы для иерархий памяти . LNCS 2625. Springer Verlag: 193–212. CiteSeerX 10.1.1.150.5426 .
^ ab Фриго, М.; Лейзерсон, К. Э .; Прокоп, Х.; Рамачандран, С. (1999). Алгоритмы, забывающие о кэше (PDF) . Труды симпозиума IEEE по основам компьютерной науки (FOCS). стр. 285–297.
^ Дэниел Слейтор, Роберт Тарджан. Амортизированная эффективность обновления списка и правил пейджинга. В Communications of the ACM , том 28, номер 2, стр. 202–208. Февраль 1985 г.
^ ab Erik Demaine . Cache-Oblivious Algorithms and Data Structures, в Lecture Notes from the EEF Summer School on Massive Data Sets, BRICS, University of Aarhus, Дания, 27 июня – 1 июля 2002 г.
^ Олсен, Джеспер Холм; Сков, Сорен Кристиан (2 декабря 2002 г.). Алгоритмы, не обращающие внимания на кэш, на практике (PDF) (магистр). Копенгагенский университет . Проверено 3 января 2022 г.
^ Вервер, Макс (23 июня 2008 г.). «Оценка структуры данных, игнорирующей кэш» (PDF) . Получено 3 января 2022 г.