Веревка (структура данных)

Структура данных для хранения строк

Простая веревка, сделанная на основе строки «Привет_меня_имя_Саймон».

В компьютерном программировании веревка или шнур — это структура данных , состоящая из меньших строк , которая используется для эффективного хранения и обработки более длинных строк или целых текстов. Например, программа редактирования текста может использовать веревку для представления редактируемого текста, чтобы такие операции, как вставка, удаление и произвольный доступ, могли выполняться эффективно. ^[1]

Описание

Веревка — это тип бинарного дерева , в котором каждый лист (конечный узел) содержит строку и длину (также известную как вес ), а каждый узел выше по дереву содержит сумму длин всех листьев в своем левом поддереве . Таким образом, узел с двумя дочерними узлами делит всю строку на две части: левое поддерево хранит первую часть строки, правое поддерево хранит вторую часть строки, а вес узла — это длина первой части.

Для операций с веревками строки, хранящиеся в узлах, предполагаются постоянными неизменяемыми объектами в типичном неразрушающем случае, что допускает некоторое поведение копирования при записи . Листовые узлы обычно реализуются как базовые строки фиксированной длины с прикрепленным счетчиком ссылок для освобождения, когда они больше не нужны, хотя можно использовать и другие методы сбора мусора .

Операции

В следующих определениях N — длина веревки, то есть вес корневого узла.

Собирайте листья

Определение: Создайте стек S и список L. Пройдите вниз по самому левому хребту дерева, пока не достигнете листа l', добавляя каждый узел n к S. Добавьте l' к L. Родительский элемент l' ( p ) находится наверху стека. Повторите процедуру для правого поддерева p.

окончательный класс InOrderRopeIterator реализует Iterator < RopeLike > {      частный финальный стек Deque < RopeLike > ;    InOrderRopeIterator ( @NonNull RopeLike root ) { stack = new ArrayDeque <> ( ); var c = root ; while ( c ! = null ) { stack.push ( c ); c = c.getLeft ( ) ; } }                       @Override public boolean hasNext ( ) { return stack.size ( ) > 0 ; }          @Override public RopeLike next () { val result = stack . pop ();         если ( ! стек . isEmpty ()) { var parent = stack . pop (); var right = parent . getRight (); если ( right != null ) { стек . push ( right ); var cleft = right . getLeft (); while ( cleft != null ) { стек . push ( cleft ); cleft = cleft . getLeft (); } } }                                 вернуть результат ; } }  

Ребалансировка

Определение: Соберите набор листьев L и восстановите дерево снизу вверх.

static boolean isBalanced ( RopeLike r ) { val depth = r.deep ( ) ; if ( deep > = FIBONACCI_SEQUENCE.length - 2 ) { return false ; } return FIBONACCI_SEQUENCE [ deep + 2 ] < = r.deep ( ) ; }                        static RopeLike rebalance ( RopeLike r ) { if ( ! isBalanced ( r )) { val leaves = Ropes . collectLeaves ( r ); return merge ( leaves , 0 , leaves . size ()); } return r ; }                  статическое слияние RopeLike ( List < RopeLike > leaves ) { return merge ( leaves , 0 , leaves . size ()); }        static RopeLike merge ( List <RopeLike> leaves , int start , int end ) { int range = end - start ; if ( range == 1 ) { return leaves.get ( start ) ; } if ( range == 2 ) { return new RopeLikeTree ( leaves.get ( start ) , leaves.get ( start + 1 ) ) ; } int mid = start + ( range / 2 ) ; return new RopeLikeTree ( merge ( leaves , start , mid ) , merge ( leaves , mid , end ) ) ; }                                                  

Вставлять

Определение: Insert(i, S’) вставить строку S', начиная с позиции i, в строку s , чтобы образовать новую строку C ₁ , ..., C _i , S' , C _{i + 1} , ..., C _m .

Временная сложность: ⁠ ⁠ ${\displaystyle O(\log N)}$ .

Эту операцию можно выполнить с помощью одной Split()и двух Concat()операций. Стоимость равна сумме трех.

public Rope insert ( int idx , CharSequence sequence ) { if ( idx == 0 ) { return prepend ( sequence ); } if ( idx == length ()) { return append ( sequence ); } val lhs = base . split ( idx ); return new Rope ( Ropes . concat ( lhs . fst . append ( sequence ), lhs . snd )); }                              

Индекс

Рисунок 2.1: Пример поиска индекса на веревке.

Определение: Index(i) : вернуть символ в позиции i

Временная сложность: ⁠ ⁠ ${\displaystyle O(\log N)}$

Чтобы извлечь i -й символ, мы начинаем рекурсивный поиск с корневого узла:

@Override public int indexOf ( char ch , int startIndex ) { if ( startIndex > weight ) { return right.indexOf ( ch , startIndex - weight ) ; } return left.indexOf ( ch , startIndex ) ; }​​                    

Например, чтобы найти символ на i=10рисунке 2.1, показанном справа, начните с корневого узла (A), найдите, что 22 больше 10 и есть левый потомок, поэтому перейдите к левому потомку (B). 9 меньше 10, поэтому вычтите 9 из 10 (оставив i=1) и перейдите к правому потомку (D). Затем, поскольку 6 больше 1 и есть левый потомок, перейдите к левому потомку (G). 2 больше 1 и есть левый потомок, поэтому снова перейдите к левому потомку (J). Наконец, 2 больше 1, но левого потомка нет, поэтому ответом является символ с индексом 1 короткой строки "na" (т. е. "n"). (индекс на основе 1)

Конкат

Рисунок 2.2: Объединение двух дочерних веревок в одну.

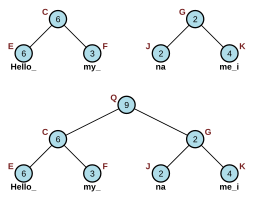
Определение Concat(S1, S2) : соединить две веревки, S ₁ и S ₂ , в одну.

Временная сложность: ⁠ ⁠ ${\displaystyle O(1)}$ (или ⁠ ⁠ ${\displaystyle O(\log N)}$ время вычисления корневого веса)

Конкатенацию можно выполнить просто путем создания нового корневого узла с левым = S1 и правым = S2 , что является постоянным временем. Вес родительского узла устанавливается равным длине левого потомка S ₁ , что займет ⁠ ⁠ время, если дерево сбалансировано. ${\displaystyle O(\log N)}$

Поскольку для большинства операций с канатами требуются сбалансированные деревья, после соединения может потребоваться повторная балансировка дерева.

Расколоть

Рисунок 2.3: Разделение веревки пополам.

Определение: Split (i, S) разделить строку S на две новые строки S ₁ и S ₂ , S ₁ = C ₁ , ..., _Ci и S 2 ₌ Ci + _{1 ,} ..., C _m .

Временная сложность: ⁠ ⁠ ${\displaystyle O(\log N)}$

Необходимо рассмотреть два случая:

1. Точка разделения находится в конце строки (т.е. после последнего символа конечного узла).
2. Точка разделения находится в середине струны.

Второй случай сводится к первому путем разделения строки в точке разделения для создания двух новых конечных узлов, а затем создания нового узла, который является родительским для двух составляющих строк.

Например, чтобы разделить 22-символьную связку, изображенную на рисунке 2.3, на две равные компонентные связку длиной 11, запросите 12-й символ, чтобы найти узел K на нижнем уровне. Удалите связь между K и G . Перейдите к родителю G и вычтите вес K из веса D . Поднимитесь по дереву и удалите все правые связи с поддеревьями, охватывающими символы после позиции 11, вычитая вес K из их родительских узлов (в данном случае только узлы D и A ). Наконец, создайте новые осиротевшие узлы K и H, объединив их вместе и создав нового родителя P с весом, равным длине левого узла K .

Поскольку для большинства операций с канатами требуются сбалансированные деревья, после раскалывания может потребоваться повторная балансировка дерева.

public Pair < ​​RopeLike , RopeLike > split ( int index ) { if ( index < weight ) { val split = left . split ( index ); return Pair . of ( rebalance ( split . fst ), rebalance ( new RopeLikeTree ( split . snd , right ))); } else if ( index > weight ) { val split = right . split ( index - weight ); return Pair . of ( rebalance ( new RopeLikeTree ( left , split . fst )), rebalance ( split . snd )); } else { return Pair . of ( left , right ); } }                                            

Удалить

Определение: Delete(i, j) удалить подстроку C _i , …, C _{i + j − 1} , из s, чтобы сформировать новую строку C ₁ , …, C _{i − 1} , C _{i + j} , …, C _m .

Временная сложность: ⁠ ⁠ ${\displaystyle O(\log N)}$ .

Эту операцию можно выполнить двумя Split()и одной Concat()операцией. Сначала разделите веревку на три, разделенные на i -й и i+j -й символ соответственно, что извлечет строку для удаления в отдельный узел. Затем соедините два других узла.

@Override public RopeLike delete ( int start , int length ) { val lhs = split ( start ) ; val rhs = split ( start + length ) ; return rebalance ( new RopeLikeTree ( lhs.fst , rhs.snd ) ) ; }                    

Отчет

Определение: Report(i, j) вывести строку C _i , …, C _{i + j − 1} .

Временная сложность: ⁠ ⁠ ${\displaystyle O(j+\log N)}$

Чтобы сообщить строку C _i , …, C _{i + j − 1} , найдите узел u , содержащий C _i и weight(u) >= j, а затем пройдите T , начиная с узла u . Выведите C _i , …, C _{i + j − 1} , выполнив упорядоченный обход T , начиная с узла u .

Сравнение с монолитными массивами

Преимущества:

• Связки позволяют гораздо быстрее вставлять и удалять текст, чем монолитные строковые массивы, операции с которыми имеют временную сложность O(n).
• Канаты не требуют O(n) дополнительной памяти при работе с ними (массивам она нужна для операций копирования).
• Веревки не требуют больших непрерывных областей памяти.
• Если используются только неразрушающие версии операций, то веревка является постоянной структурой данных . Для примера программы редактирования текста это приводит к легкой поддержке нескольких уровней отмены .

Недостатки:

• Большее общее использование пространства, когда не используется, в основном для хранения родительских узлов. Существует компромисс между тем, сколько из общей памяти является такими накладными расходами, и тем, насколько длинные фрагменты данных обрабатываются как строки. Строки в приведенных выше примерах нереалистично короткие для современных архитектур. Накладные расходы всегда O(n), но константу можно сделать произвольно малой.
• Увеличение времени на управление дополнительным хранилищем
• Повышенная сложность исходного кода; больший риск ошибок

В этой таблице сравниваются алгоритмические черты реализаций строк и веревок, а не их чистая скорость . Строки на основе массивов имеют меньшие накладные расходы, поэтому (например) операции конкатенации и разделения выполняются быстрее на небольших наборах данных. Однако, когда строки на основе массивов используются для более длинных строк, временная сложность и использование памяти для вставки и удаления символов становятся неприемлемо большими. Напротив, структура данных веревок имеет стабильную производительность независимо от размера данных. Кроме того, пространственная сложность для веревок и массивов составляет O(n). Подводя итог, веревки предпочтительны, когда данные большие и часто изменяются.

Смотрите также

• Среда программирования Cedar , которая использовала веревки «почти с момента своего создания» ^[1]
• Модель T enfilade , похожая структура данных начала 1970-х годов
• Буфер разрывов — структура данных, обычно используемая в текстовых редакторах, которая позволяет эффективно выполнять операции вставки и удаления, сгруппированные вблизи одного и того же места.
• Таблица фрагментов — еще одна структура данных, обычно используемая в текстовых редакторах.

Ссылки

1. Boehm, Hans-J; Atkinson, Russ; Plass, Michael (декабрь 1995 г.). «Веревки: альтернатива струнам» ( PDF ) . Software: Practice and Experience . 25 (12). Нью-Йорк, штат Нью-Йорк, США: John Wiley & Sons, Inc.: 1315–1330. doi :10.1002/spe.4380251203. Архивировано из оригинала 08.03.2020.
2. "Обзор реализации веревки". www.sgi.com . Архивировано из оригинала 2017-12-19 . Получено 2017-03-01 .

Внешние ссылки

• Реализация канатов "absl::Cord" в библиотеке The Abseil
• Реализация канатов «C cords» в библиотеке Boehm Garbage Collector
• Спецификация SGI C++ для веревок (поддерживается STLPort и libstdc++)
• Веревки для C#
• веревки для Common Lisp
• Канаты для Java
• Веревки-струны для Java
• Канаты для JavaScript
• Веревки для Лимбо
• веревки для Ним
• Канаты для OCaml
• пиропы для Python
• Канаты для Smalltalk
• SwiftRope для Swift
• «Ropey» для Rust