В распределенных вычислениях выбор лидера — это процесс назначения одного процесса организатором некоторой задачи, распределенной между несколькими компьютерами (узлами). До начала выполнения задачи все узлы сети либо не знают, какой узел будет «лидером» (или координатором ) задачи, либо не могут связаться с текущим координатором. Однако после запуска алгоритма выбора лидера каждый узел в сети распознает определенный, уникальный узел как лидера задачи.
Узлы сети общаются между собой, чтобы решить, кто из них попадет в состояние «лидера». Для этого им нужен какой-то метод, чтобы нарушить симметрию между ними. Например, если каждый узел имеет уникальные и сопоставимые идентификаторы, то узлы могут сравнить свои идентификаторы и решить, что узел с наивысшим идентификатором является лидером.
Определение этой проблемы часто приписывают ЛеЛанну, который формализовал ее как метод создания нового токена в сети Token Ring , в которой токен был утерян.
Алгоритмы выбора лидера разработаны так, чтобы быть экономичными с точки зрения общего числа переданных байтов и времени. Алгоритм, предложенный Галлагером, Хамблетом и Спирой [1] для общих неориентированных графов, оказал сильное влияние на разработку распределенных алгоритмов в целом и получил премию Дейкстры за влиятельную статью в области распределенных вычислений.
Было предложено много других алгоритмов для различных видов сетевых графов , таких как неориентированные кольца, однонаправленные кольца, полные графы, сетки, направленные графы Эйлера и другие. Общий метод, который отделяет проблему семейства графов от разработки алгоритма выбора лидера, был предложен Корахом, Куттеном и Мораном . [2]
Проблема выбора лидера заключается в том, что каждый процессор в конечном итоге должен решить, является ли он лидером или нет, при условии, что только один процессор решает, что он лидер. [3] Алгоритм решает задачу выбора лидера, если:
Действительный алгоритм выбора лидера должен соответствовать следующим условиям: [4]
Алгоритм выбора лидера может различаться по следующим аспектам: [5]

Кольцевая сеть — это топология связного графа, в которой каждый узел точно соединен с двумя другими узлами, т. е. для графа с n узлами существует ровно n ребер, соединяющих узлы. Кольцо может быть однонаправленным, что означает, что процессоры взаимодействуют только в одном направлении (узел может отправлять сообщения только налево или только направо), или двунаправленным, что означает, что процессоры могут передавать и получать сообщения в обоих направлениях (узел может отправлять сообщения налево и направо).
Кольцо называется анонимным, если все процессоры идентичны. Более формально, система имеет один и тот же конечный автомат для каждого процессора. [3] Не существует детерминированного алгоритма для выбора лидера в анонимных кольцах, даже когда размер сети известен процессам. [3] [6] Это связано с тем, что нет возможности нарушить симметрию в анонимном кольце, если все процессы работают с одинаковой скоростью. Состояние процессоров после некоторых шагов зависит только от начального состояния соседних узлов. Таким образом, поскольку их состояния идентичны и выполняют одни и те же процедуры, в каждом раунде каждый процессор отправляет одни и те же сообщения. Следовательно, состояние каждого процессора также изменяется идентично, и в результате, если один процессор выбирается лидером, то и все остальные тоже.
Для простоты, вот доказательство в анонимных синхронных кольцах. Это доказательство от противного. Рассмотрим анонимное кольцо R с размером n>1. Предположим, что существует алгоритм "A" для решения вопроса о выборах лидера в этом анонимном кольце R. [3]
Доказательство. Доказательство индукцией по .
Базовый случай: все процессы находятся в начальном состоянии, поэтому все процессы идентичны.
Гипотеза индукции: предположим, что лемма верна для раундов.
Индуктивный шаг: в раунде каждый процесс отправляет одно и то же сообщение направо и налево. Поскольку все процессы находятся в одном и том же состоянии после раунда , в раунде k каждый процесс получит сообщение с левого края и получит сообщение с правого края. Поскольку все процессы получают одни и те же сообщения в раунде , они находятся в одном и том же состоянии после раунда .
Приведенная выше лемма противоречит тому факту, что после некоторого конечного числа раундов выполнения A один процесс перешел в выбранное состояние, а другие процессы перешли в невыбранное состояние.
Распространенным подходом к решению проблемы выбора лидера в анонимных кольцах является использование вероятностных алгоритмов . В таких подходах процессоры обычно принимают некоторые идентичности на основе вероятностной функции и сообщают ее остальной части сети. В конце, посредством применения алгоритма, выбирается лидер (с высокой вероятностью).

Поскольку для анонимных колец не существует алгоритма (доказано выше), асинхронные кольца будут рассматриваться как асинхронные неанонимные кольца. В неанонимных кольцах каждый процесс имеет уникальный , и они не знают размер кольца. Выборы лидера в асинхронных кольцах могут быть решены некоторым алгоритмом с использованием сообщений или сообщений.
В алгоритме каждый процесс отправляет сообщение со своим на левый край. Затем ждет, пока не придет сообщение с правого края. Если в сообщении больше, чем его собственное , то пересылает сообщение на левый край; в противном случае игнорирует сообщение и ничего не делает. Если в сообщении равно его собственному , то отправляет сообщение налево, объявляя себя избранным. Другие процессы пересылают объявление налево и сами становятся неизбранными. Очевидно, что верхняя граница для этого алгоритма.
В алгоритме он выполняется по фазам. На фазе th процесс определит, является ли он победителем среди соседей слева и справа . Если он победитель, то процесс может перейти к следующей фазе. На фазе , каждый процесс должен определить, является ли он победителем или нет, отправив сообщение своим соседям слева и справа (соседи не пересылают сообщение). Сосед отвечает только в том случае, если в сообщении больше, чем у соседа , в противном случае отвечает . Если получает два s, один слева, один справа, то является победителем на фазе . На фазе победители на фазе должны отправить сообщение своим соседям слева и справа. Если соседи на пути получают в сообщении больше, чем их , то пересылают сообщение следующему соседу, в противном случае отвечают . Если сосед th получает больше, чем его , то отправляет обратно , в противном случае отвечает . Если процесс получает два s, то он является победителем на фазе . В последней фазе окончательный победитель получит свое в сообщении, затем завершается и отправляет сообщение о завершении другим процессам. В худшем случае в каждой фазе есть не более победителей, где — номер фазы. Всего фаз. Каждый победитель отправляет сообщения в порядке их поступления в каждой фазе. Таким образом, сложность сообщений составляет .
В книге Аттия и Уэлча «Распределенные вычисления» [3] они описали неоднородный алгоритм, использующий сообщения в синхронном кольце с известным размером кольца . Алгоритм работает по фазам, каждая фаза имеет раунды, каждый раунд — это одна единица времени. В фазе , если есть процесс с , то процесс отправляет сообщение о завершении другим процессам (отправка сообщений о завершении стоит раундов). В противном случае, перейти к следующей фазе. Алгоритм проверит, есть ли фаза с номером, равным процессу , затем выполнит те же шаги, что и фаза . В конце выполнения минимальное будет выбрано лидером. Он использовал ровно сообщений и раундов.
Итай и Родех [7] представили алгоритм для однонаправленного кольца с синхронизированными процессами. Они предполагают, что размер кольца (количество узлов) известен процессам. Для кольца размером n активны a≤n процессоров. Каждый процессор решает с вероятностью a^(-1), стать ли кандидатом. В конце каждой фазы каждый процессор вычисляет количество кандидатов c, и если оно равно 1, он становится лидером. Чтобы определить значение c, каждый кандидат отправляет токен (камешек) в начале фазы, который передается по кольцу, возвращаясь ровно через n единиц времени своему отправителю. Каждый процессор определяет c, подсчитывая количество прошедших камешков. Этот алгоритм достигает выбора лидера с ожидаемой сложностью сообщения O(nlogn). Также используется аналогичный подход, в котором механизм тайм-аута используется для обнаружения тупиков в системе. [8] Существуют также алгоритмы для колец специальных размеров, таких как простой размер [9] [10] и нечетный размер. [11]
В типичных подходах к выбору лидера предполагается, что размер кольца известен процессам. В случае анонимных колец, без использования внешней сущности, невозможно выбрать лидера. Даже если предположить, что алгоритм существует, лидер не может оценить размер кольца. т. е. в любом анонимном кольце существует положительная вероятность того, что алгоритм вычислит неправильный размер кольца. [12] Чтобы преодолеть эту проблему, Фишер и Цзян использовали так называемый оракул лидера Ω?, который каждый процессор может спросить, есть ли уникальный лидер. Они показывают, что с некоторой точки и выше он гарантированно вернет один и тот же ответ всем процессам. [13]
В одной из ранних работ Чанг и Робертс [14] предложили единый алгоритм, в котором процессор с наивысшим идентификатором выбирается в качестве лидера. Каждый процессор отправляет свой идентификатор по часовой стрелке. Процесс получает сообщение и сравнивает его со своим собственным. Если оно больше, он пропускает его, в противном случае он отбрасывает сообщение. Они показывают, что этот алгоритм использует максимум сообщений и в среднем случае. Хиршберг и Синклер [15] улучшили этот алгоритм со сложностью сообщений, введя схему передачи сообщений в двух направлениях, позволяющую процессорам отправлять сообщения в обоих направлениях.

Сетка — еще одна популярная форма сетевой топологии, особенно в параллельных системах, системах избыточной памяти и сетях взаимосвязей. [16]
В сетчатой структуре узлы являются либо угловыми (только два соседа), либо граничными (только три соседа), либо внутренними (с четырьмя соседями). Количество ребер в сетке размером axb равно m=2ab-ab.
Типичный алгоритм решения проблемы выбора лидера в неориентированной сетке состоит в том, чтобы выбрать только один из четырех угловых узлов в качестве лидера. Поскольку угловые узлы могут не знать о состоянии других процессов, алгоритм должен сначала разбудить угловые узлы. Лидер может быть выбран следующим образом. [17]
Сложность сообщения не превышает , а если сетка имеет квадратную форму, .
Ориентированная сетка — это особый случай, где номера портов — это метки компаса, то есть север, юг, восток и запад. Выбор лидера в ориентированной сетке тривиален. Нам нужно только назначить угол, например «север» и «восток», и убедиться, что узел знает, что он лидер.

Частным случаем архитектуры сетки является тор, который представляет собой сетку с «обёртыванием». В этой структуре каждый узел имеет ровно 4 соединительных ребра. Один из подходов к выбору лидера в такой структуре известен как избирательные этапы. Подобно процедурам в кольцевых структурах, этот метод на каждом этапе исключает потенциальных кандидатов, пока в конечном итоге не останется один узел-кандидат. Этот узел становится лидером и затем уведомляет все остальные процессы о завершении. [16] Этот подход может быть использован для достижения сложности O(n). Также введены более практичные подходы для работы с наличием неисправных связей в сети. [18] [19]
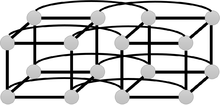
Гиперкуб — это сеть, состоящая из узлов , каждый со степенью и рёбер. Аналогичные этапы выборов, как и прежде, можно использовать для решения проблемы выбора лидера. На каждом этапе соревнуются два узла (называемые дуэлянтами), и победитель продвигается на следующий этап. Это означает, что на каждом этапе только половина дуэлянтов переходит на следующий этап. Эта процедура продолжается до тех пор, пока не останется только один дуэлянт, и он становится лидером. После выбора он уведомляет все остальные процессы. Этот алгоритм требует сообщений. В случае неориентированных гиперкубов можно использовать аналогичный подход, но с более высокой сложностью сообщений . [16]

Полные сети — это структуры, в которых все процессы связаны друг с другом, т. е. степень каждого узла равна n-1, где n — размер сети. Известно оптимальное решение с O(n) сложностью сообщений и пространства. [20] В этом алгоритме процессы имеют следующие состояния:
Предполагается, что хотя узел не знает всего набора узлов в системе, требуется, чтобы в этой схеме каждый узел знал идентификатор своего единственного преемника, который называется соседом, [20] и каждый узел был известен другому узлу. [21]
Все процессоры изначально запускаются в пассивном состоянии, пока не будут разбужены. Как только узлы просыпаются, они становятся кандидатами на роль лидера. На основе схемы приоритетов узлы-кандидаты сотрудничают в виртуальном кольце. В какой-то момент кандидаты узнают о личности кандидатов, которые предшествуют им в кольце. Кандидаты с более высоким приоритетом спрашивают у кандидатов с более низким приоритетом об их предшественниках. Кандидаты с более низким приоритетом становятся подставными лицами после ответа кандидатам с более высоким приоритетом. На основе этой схемы кандидат с самым высоким приоритетом в конечном итоге узнает, что все узлы в системе являются подставными лицами, кроме него самого, и в этот момент он знает, что является лидером.
Приведенный выше алгоритм неверен — он нуждается в дальнейшем улучшении. [21]
Как следует из названия, эти алгоритмы предназначены для использования в любой форме технологических сетей без каких-либо предварительных знаний о топологии сети или ее свойствах, таких как ее размер. [16]
Shout (протокол) строит остовное дерево на общем графе и выбирает его корень в качестве лидера. Алгоритм имеет общую стоимость, линейную по мощности ребер.
Этот метод по сути похож на поиск минимального остовного дерева (MST), в котором корень дерева становится лидером. Основная идея этого метода заключается в том, что отдельные узлы сливаются друг с другом для формирования более крупных структур. Результатом этого алгоритма является дерево (граф без цикла), корень которого является лидером всей системы. Стоимость метода мегаслияния составляет где m — количество ребер, а n — количество узлов.

Yo-yo (алгоритм) — это алгоритм поиска минимума, состоящий из двух частей: фазы предварительной обработки и серии итераций. [16] На первой фазе или настройке каждый узел обменивается своим идентификатором со всеми своими соседями и на основе значения ориентирует свои инцидентные ребра. Например, если узел x имеет меньший идентификатор, чем y, x ориентируется по направлению к y. Если узел имеет меньший идентификатор, чем все его соседи, он становится источником . Напротив, узел со всеми внутренними ребрами (т. е. с идентификатором, большим, чем у всех его соседей) является стоком . Все остальные узлы являются внутренними узлами.
Как только все ребра ориентированы, начинается фаза итерации . Каждая итерация является избирательным этапом, на котором некоторые кандидаты будут удалены. Каждая итерация имеет две фазы: YO- и –YO . На этой фазе источники начинают процесс распространения на каждый приемник наименьших значений источников, подключенных к этому приемнику.
Йо-
-йоу
После финальной стадии любой источник, который получает НЕТ, больше не является источником и становится стоком. Дополнительный этап, обрезка , также вводится для удаления узлов, которые бесполезны, т.е. их существование не влияет на следующие итерации.
Этот метод имеет общую стоимость O(mlogn) сообщений. Его реальная сложность сообщений, включая обрезку, является открытой исследовательской проблемой и неизвестна.
В протоколах радиосетей выбор лидера часто используется в качестве первого шага для приближения к более продвинутым примитивам связи, таким как сбор сообщений или трансляции. [22] Сама природа беспроводных сетей вызывает коллизии, когда соседние узлы передают данные одновременно; выбор лидера позволяет лучше координировать этот процесс. В то время как диаметр D сети является естественной нижней границей для времени, необходимого для выбора лидера, верхняя и нижняя границы для проблемы выбора лидера зависят от конкретной изучаемой модели радио.
В радиосетях n узлов могут в каждом раунде выбирать, передавать или получать сообщение. Если обнаружение столкновений недоступно , то узел не может отличить тишину от получения более одного сообщения за раз. Если обнаружение столкновений доступно, то узел может обнаружить более одного входящего сообщения одновременно, даже если сами сообщения не могут быть декодированы в этом случае. В модели звукового сигнала узлы могут отличить тишину или по крайней мере одно сообщение только с помощью зондирования несущей .
Известные времена выполнения для сетей с одним переходом варьируются от константы (ожидается с обнаружением столкновений) до O(n log n) раундов (детерминированные и без обнаружения столкновений). В сетях с несколькими переходами известные времена выполнения различаются от примерно O((D+ log n)(log 2 log n)) раундов (с высокой вероятностью в модели звукового сигнала), O(D log n) (детерминированные в модели звукового сигнала), O(n) (детерминированные с обнаружением столкновений) до O(n log 3/2 n (log log n) 0.5 ) раундов (детерминированные и без обнаружения столкновений).
{{cite journal}}: CS1 maint: multiple names: authors list (link){{cite journal}}: CS1 maint: multiple names: authors list (link){{cite book}}: |journal=проигнорировано ( помощь )