Вертикальное изменение давления

Вертикальное изменение давления — это изменение давления как функции высоты . В зависимости от рассматриваемой жидкости и контекста, на который она ссылается, она также может значительно изменяться в измерениях, перпендикулярных высоте, и эти изменения имеют значение в контексте силы градиента давления и ее эффектов. Однако вертикальное изменение особенно значимо, поскольку оно является результатом воздействия силы тяжести на жидкость; а именно, для той же данной жидкости уменьшение высоты внутри нее соответствует более высокому столбу жидкости, давящему на эту точку.

Основная формула

Относительно простая версия ^[1] вертикального изменения давления жидкости заключается в том, что разница давления между двумя высотами является произведением изменения высоты, силы тяжести и плотности . Уравнение выглядит следующим образом: где ${\frac {dP}{dh}}=-\rho g,$

$P$ — давление,
$ρ$ — плотность,
$g$ — ускорение свободного падения , а
$h$ — высота.

Символ дельта указывает на изменение заданной переменной. Поскольку $g$ отрицательно, увеличение высоты будет соответствовать уменьшению давления, что соответствует ранее упомянутому рассуждению о весе столба жидкости.

Когда плотность и сила тяжести приблизительно постоянны (то есть, для относительно небольших изменений высоты), простое умножение разницы высот, силы тяжести и плотности даст хорошее приближение разницы давлений. Если известно, что давление в одной точке жидкости с однородной плотностью ρ равно P ₀ , то давление в другой точке равно P ₁ :

P_{1}=P_{0}-\rho g(h_{1}-h_{0})

где h ₁ - h ₀ — вертикальное расстояние между двумя точками. ^[2]

Если различные жидкости накладываются друг на друга слоями, то общая разность давлений будет получена путем сложения двух разностей давлений; первая — от точки 1 до границы, вторая — от границы до точки 2; что просто включает в себя замену значений $ρ$ и $Δ h$ для каждой жидкости и суммирование результатов. Если плотность жидкости меняется с высотой, потребуется математическое интегрирование .

То, можно ли разумно аппроксимировать плотность и гравитацию как константы, зависит от необходимого уровня точности , а также от масштаба длины разницы высот, поскольку гравитация и плотность также уменьшаются с увеличением высоты. Для плотности, в частности, также имеет значение рассматриваемая жидкость; например, морская вода считается несжимаемой жидкостью ; ее плотность может меняться с высотой, но гораздо менее значительно, чем плотность воздуха. Таким образом, плотность воды можно разумнее аппроксимировать как константу, чем плотность воздуха, и при одинаковой разнице высот перепады давления в воде примерно равны на любой высоте.

Гидростатический парадокс

Барометрическая формула зависит только от высоты жидкостной камеры, а не от ее ширины или длины. При достаточно большой высоте может быть достигнуто любое давление. Эта особенность гидростатики была названа гидростатическим парадоксом . Как выразился WH Besant , ^[3]

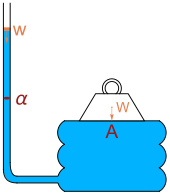
Любое количество жидкости, каким бы малым оно ни было, может выдерживать любой вес, каким бы большим он ни был.

Фламандский ученый Саймон Стевин был первым, кто объяснил этот парадокс математически. ^[4] В 1916 году Ричард Глейзбрук упомянул гидростатический парадокс, описывая конструкцию, которую он приписывал Паскалю : тяжелый груз $W$ покоится на доске площадью $A,$ покоящейся на жидкостном пузыре, соединенном с вертикальной трубкой с площадью поперечного сечения α. Выливание воды весом $w$ вниз по трубке в конечном итоге поднимет тяжелый груз. Баланс сил приводит к уравнению

W={\frac {wA}{\alpha }}.

Глейзбрук говорит: «Сделав площадь доски значительной, а площадь трубки — малой, можно выдержать большой вес $W с помощью малого веса$ $w$ воды. Этот факт иногда называют гидростатическим парадоксом». ^[5]

Гидравлические машины используют это явление для умножения силы или крутящего момента. Демонстрации гидростатического парадокса используются при обучении этому явлению. ^[6]^[7]

В контексте атмосферы Земли

Если проанализировать вертикальные изменения давления в атмосфере Земли , то масштаб длины очень значителен ( одна только тропосфера имеет высоту в несколько километров ; термосфера — в несколько сотен километров), а вовлеченная жидкость (воздух) сжимаема. Гравитацию все еще можно разумно аппроксимировать как постоянную, поскольку масштабы длины порядка километров все еще малы по сравнению с радиусом Земли, который в среднем составляет около 6371 км, ^[8] а гравитация является функцией расстояния от ядра Земли. ^[9]

Плотность, с другой стороны, меняется более существенно с высотой. Из закона идеального газа следует , что где $\rho ={\frac {mP}{kT}},$

$m$ — средняя масса на молекулу воздуха ,
$P$ — давление в данной точке,
$k$ — постоянная Больцмана ,
$T$ — температура в градусах Кельвина .

Проще говоря, плотность воздуха зависит от давления воздуха. Учитывая, что давление воздуха также зависит от плотности воздуха, легко может сложиться впечатление, что это было круговое определение , но это просто взаимозависимость различных переменных. Это затем дает более точную формулу вида где $P_{h}=P_{0}e^{-{\frac {mgh}{kT}}},$

$P h$ — давление на высоте $h$ ,
$P 0$ — давление в точке отсчета 0 (обычно относится к уровню моря),
$m$ — масса на молекулу воздуха,
$g$ — ускорение свободного падения ,
$h$ - высота от точки отсчета 0,
$k$ — постоянная Больцмана ,
$T$ — температура в градусах Кельвина.

Таким образом, вместо того, чтобы давление было линейной функцией высоты, как можно было бы ожидать из более простой формулы, приведенной в разделе «Основная формула», более точно его можно представить как экспоненциальную функцию высоты.

Обратите внимание, что в этом упрощении температура рассматривается как постоянная, хотя температура также меняется с высотой. Однако изменение температуры в нижних слоях атмосферы ( тропосфера , стратосфера ) составляет всего лишь десятки градусов, в отличие от их термодинамической температуры , которая составляет сотни, поэтому изменение температуры достаточно мало и, таким образом, игнорируется. Для меньших перепадов высот, включая перепады сверху донизу даже самых высоких зданий (например, CN Tower ) или для гор сопоставимого размера, изменение температуры будет легко находиться в пределах однозначных чисел. (См. также градиент скорости .)

Альтернативный вывод, представленный Портлендским государственным аэрокосмическим обществом ^[10] , используется для того, чтобы вместо этого задать высоту как функцию давления. Это может показаться нелогичным, поскольку давление является результатом высоты, а не наоборот, но такая формула может быть полезна для нахождения высоты на основе разницы давления, когда известно последнее, а не первое. Для разных видов приближений представлены различные формулы; для сравнения с предыдущей формулой первой из упомянутых в статье будет та, которая применяет то же приближение постоянной температуры; в этом случае: где (со значениями, используемыми в статье) $z=-{\frac {RT}{g}}\ln {\frac {P}{P_{0}}}$

$z$ — высота в метрах,
$R$ — удельная газовая постоянная =287,053 Дж/(кг К)
$T$ — абсолютная температура в градусах Кельвина =288,15 К на уровне моря,
$g$ — ускорение свободного падения =9,806 65 м/с ² на уровне моря,
$P$ — давление в заданной точке на высоте $z$ в Паскалях , а
$P 0$ — давление в точке отсчета =101 325 Па на уровне моря.

Более общая формула, выведенная в той же статье, учитывает линейное изменение температуры в зависимости от высоты (градиент температуры) и сводится к приведенной выше формуле, когда температура постоянна: где $z={\frac {T_{0}}{L}}\left(\left({\frac {P}{P_{0}}}\right)^{-{\frac {LR}{g}}}-1\right)$

$L$ — атмосферный градиент температуры (изменение температуры, деленное на расстояние) =−6,5 × 10 ⁻³ К/м , и
$T 0$ — температура в той же точке отсчета, для которой $P = P 0$

и другие величины те же, что и выше. Это рекомендуемая формула для использования.

Смотрите также

Ссылки

^ «Барометрическая формула».
^ Стритер, Виктор Л. (1966). Механика жидкости , 4-е издание, стр. 28, McGraw-Hill
^ Besant, WH (1900). Elementary Hydrostatics. George Bell & Sons . стр. 11 – через Internet Archive .
^ Ру, Софи (25 сентября 2012 г.). Механизация натуральной философии . Springer Science & Business Media. стр. 160. ISBN 978-9400743458. Стевин дает оригинальную математическую демонстрацию так называемого гидростатического парадокса.
^ Глейзбрук, Ричард (1916). Гидростатика: элементарный учебник, теоретический и практический. Cambridge University Press . стр. 42 – через Интернет-архив .
^ Гринслейд-младший, Томас Б. «Гидростатический парадокс». Колледж Кеньон .
^ Объяснение на YouTube
^ "Радиус Земли". 2 марта 2009 г.
^ "Закон тяготения Ньютона". www.splung.com . Получено 23 июня 2023 г. .
^ "Быстрый вывод, связывающий высоту с давлением воздуха" (PDF) . Архивировано из оригинала (PDF) 2011-09-28 . Получено 2011-11-30 .

Мерлино, Роберт Л. (2003). "Статика – Жидкости в состоянии покоя" . Получено 2014-11-20 .

Внешние ссылки

Медиа, связанные с Гидростатическим парадоксом на Wikimedia Commons