куб Гильберта

Тип топологического пространства

В математике куб Гильберта , названный в честь Дэвида Гильберта , является топологическим пространством , которое представляет собой поучительный пример некоторых идей топологии . Кроме того, многие интересные топологические пространства могут быть вложены в куб Гильберта; то есть могут рассматриваться как подпространства куба Гильберта (см. ниже).

Определение

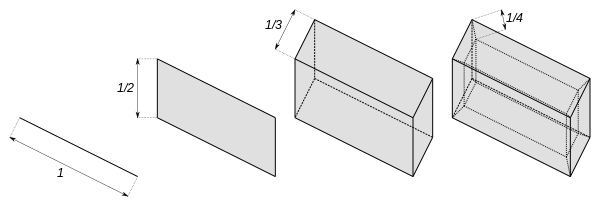
Куб Гильберта лучше всего определить как топологическое произведение интервалов для То есть, это кубоид счетно - бесконечной размерности , где длины ребер в каждом ортогональном направлении образуют последовательность ${\displaystyle [0,1/n]}$ ${\displaystyle n=1,2,3,4,\ldots .}$ ${\displaystyle \lbrace 1/n\rbrace _{n\in \mathbb {N} }.}$

Куб Гильберта гомеоморфен произведению счетно бесконечного числа копий единичного интервала Другими словами, он топологически неотличим от единичного куба счетно бесконечной размерности. Некоторые авторы используют термин «куб Гильберта» для обозначения этого декартова произведения вместо произведения . ^[1] ${\displaystyle [0,1].}$ ${\displaystyle \left[0,{\tfrac {1}{n}}\right]}$

Если точка в кубе Гильберта задана последовательностью с , то гомеоморфизм бесконечномерному единичному кубу задается формулой ${\displaystyle \lbrace a_{n}\rbrace }$ ${\displaystyle 0\leq a_{n}\leq 1/n,}$ ${\displaystyle h(a)_{n}=n\cdot a_{n}.}$

Куб Гильберта как метрическое пространство

Иногда удобно думать о кубе Гильберта как о метрическом пространстве , на самом деле как об определенном подмножестве сепарабельного пространства Гильберта (то есть, о пространстве Гильберта со счетно бесконечным базисом Гильберта). Для этих целей лучше не думать о нем как о произведении копий , а вместо этого как о, как указано выше, для топологических свойств это не имеет значения. То есть, элемент куба Гильберта является бесконечной последовательностью , которая удовлетворяет ${\displaystyle [0,1],}$ $${\displaystyle [0,1]\times [0,1/2]\times [0,1/3]\times \cdots ;}$$ $${\displaystyle \left(x_{n}\right)}$$ $${\displaystyle 0\leq x_{n}\leq 1/n.}$$

Любая такая последовательность принадлежит пространству Гильберта, поэтому куб Гильберта наследует метрику оттуда. Можно показать, что топология, индуцированная метрикой, совпадает с топологией произведения в приведенном выше определении. ${\displaystyle \ell _{2},}$

Характеристики

Как произведение компактных хаусдорфовых пространств , гильбертов куб сам является компактным хаусдорфовым пространством в результате теоремы Тихонова . Компактность гильбертова куба можно доказать и без аксиомы выбора , построив непрерывную функцию из обычного множества Кантора на гильбертовом кубе.

Ни в одной точке нет компактной окрестности (таким образом, не является локально компактной ). Можно было бы ожидать, что все компактные подмножества конечномерны. Куб Гильберта показывает, что это не так. Но куб Гильберта не может быть окрестностью какой-либо точки, потому что его сторона становится все меньше и меньше в каждом измерении, так что открытый шар вокруг любого фиксированного радиуса должен выходить за пределы куба в некотором измерении. ${\displaystyle \ell _{2},}$ ${\displaystyle \ell _{2}}$ ${\displaystyle \ell _{2}}$ ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle e>0}$

Любое бесконечномерное выпуклое компактное подмножество гомеоморфно кубу Гильберта. Куб Гильберта — это выпуклое множество, охватывающее все пространство, но внутренность которого пуста. Такая ситуация невозможна в конечных размерностях. Касательный конус к кубу в нулевом векторе — все пространство. ${\displaystyle \ell _{2}}$

Каждое подмножество куба Гильберта наследует от куба Гильберта свойства быть как метризуемым (и, следовательно, T4 ), так и быть счетно-второстепенным . Более интересно, что обратное также верно: каждое счетно-второстепенное пространство T4 гомеоморфно подмножеству куба Гильберта.

Каждое G _δ -подмножество куба Гильберта является польским пространством , топологическим пространством, гомеоморфным сепарабельному и полному метрическому пространству. Обратно, каждое польское пространство гомеоморфно G _δ -подмножеству куба Гильберта. ^[2]

Смотрите также

• Список топологий  – Список конкретных топологий и топологических пространств

Примечания

1. Фридман 1981, стр. 221.
2. Шривастава 1998, стр. 55.

Ссылки

• Фридман, Харви (1981). «О необходимом использовании абстрактной теории множеств» (PDF) . Advances in Mathematics . 41 (3): 209–280. doi : 10.1016/0001-8708(81)90021-9 . Получено 19 декабря 2022 г. .
• Шривастава, Шаши Мохан (1998). Курс по борелевским множествам. Graduate Texts in Mathematics . Springer-Verlag . ISBN 978-0-387-98412-4. Получено 2008-12-04 .
• «Die Homoiomorphie der kompakten konvexen Mengen im Hilbertschen Raum» [Гомоморфизм компактных выпуклых множеств в гильбертовом пространстве] (на немецком языке). ЕСДМЛ. Архивировано из оригинала 02 марта 2020 г.

Дальнейшее чтение

• Стин, Линн Артур ; Зеебах, Дж. Артур-младший (1995) [1978]. Контрпримеры в топологии ( переиздание Дувра 1978 г.). Берлин, Нью-Йорк: Springer-Verlag . ISBN 978-0-486-68735-3. МР  0507446.