Гипотеза Андрицы

Графическое доказательство гипотезы Андрицы для первых (a)100, (b)200 и (c)500 простых чисел. Предполагается, что функция всегда меньше 1. ${\displaystyle A_{n}}$

Гипотеза Андрицы (названная в честь румынского математика Дорина Андрицы) — это гипотеза относительно промежутков между простыми числами . ^[1]

Гипотеза утверждает, что неравенство

${\displaystyle {\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}<1}$

справедливо для всех , где — n- е простое число. Если обозначает n- й простой пробел , то гипотезу Андрицы можно также переписать как ${\displaystyle n}$ ${\displaystyle p_{n}}$ ${\displaystyle g_{n}=p_{n+1}-p_{n}}$

${\displaystyle g_{n}<2{\sqrt {p_{n}}}+1.}$

Эмпирические данные

Имран Гори использовал данные о самых больших простых пробелах, чтобы подтвердить гипотезу до 1,3002 × 10 ¹⁶ . ^[2] Используя таблицу максимальных пробелов и указанное выше неравенство пробелов, значение подтверждения можно полностью расширить до 4 × 10 ¹⁸ . ${\displaystyle n}$

Дискретная функция представлена ​​на рисунках напротив. Высшие точки для наблюдаются при n  = 1, 2 и 4, при A ₄ ≈ 0,670873..., при этом среди первых 10 ⁵ простых чисел нет большего значения. Поскольку функция Андрики асимптотически убывает с ростом n , необходим разрыв простых чисел все большего размера, чтобы сделать разницу большой с ростом n . Поэтому весьма вероятно, что гипотеза верна, хотя это еще не доказано. ${\displaystyle A_{n}={\sqrt {p_{n+1}}}-{\sqrt {p_{n}}}}$ ${\displaystyle A_{n}}$

Обобщения

Значение x в обобщенной гипотезе Андрицы для первых 100 простых чисел, с обозначением предполагаемого значения x _min .

В качестве обобщения гипотезы Андрицы было рассмотрено следующее уравнение:

${\displaystyle p_{n+1}^{x}-p_{n}^{x}=1,}$

где — n- е простое число, а x может быть любым положительным числом. ${\displaystyle p_{n}}$

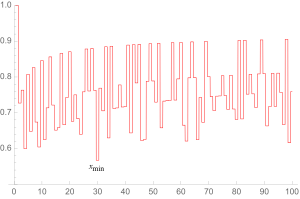
Легко видеть, что наибольшее возможное решение для x имеет место при n = 1, когда x _max  = 1. Наименьшее решение для x предположительно равно x _min  ≈ 0,567148... (последовательность A038458 в OEIS ), что имеет место при n  = 30.

Эта гипотеза также была сформулирована как неравенство , обобщенная гипотеза Андрики:

${\displaystyle p_{n+1}^{x}-p_{n}^{x}<1}$для ${\displaystyle x<x_{\min }.}$

Смотрите также

• Гипотеза Крамера
• гипотеза Лежандра
• Гипотеза Фирузбахта

Ссылки и примечания

1. Андрика, Д. (1986). «Заметка о гипотезе в теории простых чисел». Studia Univ. Babes–Bolyai Math . 31 (4): 44–48. ISSN  0252-1938. Zbl  0623.10030.
2. Уэллс, Дэвид (18 мая 2005 г.). Простые числа: самые загадочные цифры в математике . Хобокен (Нью-Джерси): Wiley. стр. 13. ISBN 978-0-471-46234-7.

• Гай, Ричард К. (2004). "Раздел A8". Нерешенные проблемы теории чисел (3-е изд.). Springer-Verlag . ISBN 978-0-387-20860-2. Збл  1058.11001.

Внешние ссылки

• Гипотеза Андрики в PlanetMath
• Обобщенная гипотеза Андрики на PlanetMath
• Вайсштейн, Эрик В. «Гипотеза Андрики». Математический мир .