stringtranslate.com

Круговая диаграмма

Круговая диаграмма численности носителей английского языка

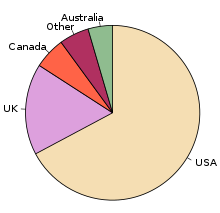
Круговая диаграмма (или круговая диаграмма ) — это круговая статистическая диаграмма , которая разделена на срезы для иллюстрации числовой пропорции. В круговой диаграмме длина дуги каждого среза (и, следовательно, его центральный угол и площадь ) пропорциональны количеству, которое она представляет. Хотя она названа так из-за своего сходства с пирогом , который был разрезан, существуют вариации в способе ее представления. Самая ранняя известная круговая диаграмма обычно приписывается « Статистическому бревиарию» Уильяма Плейфэра 1801 года. [1] [2]

Круговые диаграммы очень широко используются в деловом мире и средствах массовой информации. [3] Однако они подвергались критике, [4] и многие эксперты рекомендуют избегать их, [5] [6] [7] [8] поскольку исследования показали, что трудно сравнивать различные разделы данной круговой диаграммы или сравнивать данные на разных круговых диаграммах. Круговые диаграммы в большинстве случаев можно заменить другими графиками, такими как столбчатая диаграмма , ящичная диаграмма , точечная диаграмма и т. д.

История

Самая ранняя известная круговая диаграмма обычно приписывается «Статистическому бревиарию» Уильяма Плейфера 1801 года, в котором используются два таких графика. [1] [2] [9] Плейфер представил иллюстрацию, которая содержала ряд круговых диаграмм. Одна из этих диаграмм изображала пропорции Турецкой империи, расположенной в Азии , Европе и Африке до 1789 года. Это изобретение поначалу не получило широкого распространения. [1]

Плейфэр считал, что круговым диаграммам необходимо третье измерение для добавления дополнительной информации. [10]

Флоренс Найтингейл, возможно, не изобрела круговую диаграмму, но она адаптировала ее, чтобы сделать ее более читаемой, что способствовало ее широкому использованию и по сей день. Найтингейл перенастроила круговую диаграмму, сделав длину клиньев переменной вместо их ширины. Таким образом, график напоминал петушиный гребень. [11] Позже предполагалось, что она создала его из-за неясности и отсутствия практичности творения Плейфера. [12] Диаграмма полярных областей Найтингейл , [13] : 107  или иногда диаграмма розы Найтингейл , эквивалент современной круговой гистограммы , для иллюстрации сезонных источников смертности пациентов в военном полевом госпитале, которым она управляла, была опубликована в «Заметках о вопросах, влияющих на здоровье, эффективность и управление больницами британской армии» и отправлена ​​королеве Виктории в 1858 году. По словам историка Хью Смолла, «она, возможно, была первой, кто использовал [круговые диаграммы] для убеждения людей в необходимости перемен». [11]

Французский инженер Шарль Жозеф Минар также использовал круговые диаграммы в 1858 году. На его карте 1858 года круговые диаграммы использовались для представления скота, отправленного со всей Франции для потребления в Париже .

Ранние типы круговых диаграмм в 19 веке
  • Круговые диаграммы из «Статистического требника» Уильяма Плейфера, 1801 г.
    Круговые диаграммы из «Статистического требника» Уильяма Плейфера, 1801 г.
  • Одна из самых ранних круговых диаграмм, 1801 г.
    Одна из самых ранних круговых диаграмм, 1801 г.
  • Карта Минара, 1858 г.
    Карта Минара, 1858 г.
  • Полярная карта Флоренс Найтингейл, 1858 г.
    Полярная карта Флоренс Найтингейл , 1858 г.

Варианты и похожие диаграммы

Трехмерная круговая диаграмма и перспективный пирог

Трехмерная круговая диаграмма, или перспективная круговая диаграмма, используется для придания диаграмме трехмерного вида. Часто используемое по эстетическим причинам третье измерение не улучшает чтение данных; напротив, эти графики трудно интерпретировать из-за искаженного эффекта перспективы, связанного с третьим измерением. Использование лишних измерений, не используемых для отображения интересующих данных, не рекомендуется для диаграмм в целом, а не только для круговых диаграмм. [7] [14]

Кольцевая диаграмма

Информация о данных в целом в центре кольцевой диаграммы

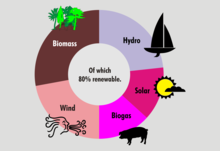
Кольцевая диаграмма (также пишется donut) — это вариант круговой диаграммы с пустым центром, позволяющим включать дополнительную информацию о данных в целом. [15] [16] Кольцевые диаграммы похожи на круговые диаграммы в том, что их цель — проиллюстрировать пропорции. [ необходима ссылка ] Этот тип круговой диаграммы может поддерживать несколько статистик одновременно и обеспечивает лучшее соотношение интенсивности данных по сравнению со стандартными круговыми диаграммами. [16] Он не обязательно должен содержать информацию в центре.

Развернутая круговая диаграмма

Развернутая круговая диаграмма для примера данных (см. ниже), на которой показана крупнейшая партийная группа.

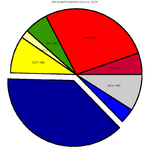
Диаграмма с одним или несколькими секторами, отделенными от остального диска, называется взорванной круговой диаграммой . Этот эффект используется либо для выделения сектора, либо для выделения меньших сегментов диаграммы с малыми пропорциями.

Диаграмма полярной области

« Диаграмма причин смертности в армии на Востоке » Флоренс Найтингейл.
Как и обычные круговые диаграммы, круговая диаграмма переменного радиуса имеет клинья, площади которых представляют общие количества в соответствующих категориях/группах. Однако здесь каждый радиус представляет количество этого количества на единицу в пределах этой категории. В этом примере площадь каждого клина представляет общие выбросы CO2 всех людей в этой категории, а каждый радиус представляет выбросы на человека в пределах этой категории.

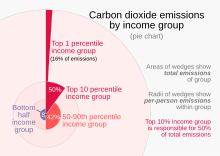
Диаграмма полярных областей похожа на обычную круговую диаграмму, за исключением того, что секторы имеют равные углы и отличаются скорее тем, насколько далеко каждый сектор простирается от центра круга. Диаграмма полярных областей используется для построения графика циклических явлений (например, количества смертей по месяцам). Например, если необходимо построить график количества смертей в каждом месяце в течение года, то будет 12 секторов (по одному в месяц), все с одинаковым углом в 30 градусов каждый. Радиус каждого сектора будет пропорционален квадратному корню из уровня смертности за месяц, поэтому площадь сектора представляет уровень смертности за месяц. Если уровень смертности в каждом месяце разделить по причине смерти, можно сделать несколько сравнений на одной диаграмме, как это видно на диаграмме полярных областей, разработанной Флоренс Найтингейл .

Первое известное использование диаграмм полярных областей было сделано Андре-Мишелем Герри , который назвал их courbes circulaires (круговые кривые) в статье 1829 года, показывающей сезонные и суточные изменения направления ветра в течение года, а также рождения и смерти по часам дня. [17] Леон Лаланн позже использовал полярную диаграмму, чтобы показать частоту направлений ветра вокруг точек компаса в 1843 году. Роза ветров до сих пор используется метеорологами . Найтингейл опубликовала свою розовую диаграмму в 1858 году. Хотя название «coxcomb» стало ассоциироваться с этим типом диаграммы, Найтингейл изначально использовала термин для обозначения публикации, в которой эта диаграмма впервые появилась — привлекающей внимание книги карт и таблиц — а не этого конкретного типа диаграммы. [18]

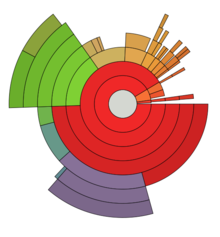
Кольцевая диаграмма, диаграмма «солнечные лучи» и многоуровневая круговая диаграмма

Многоуровневая круговая диаграмма, отображающая использование диска в файловой системе Linux

Кольцевая диаграмма, также известная как диаграмма солнечных лучей или многоуровневая круговая диаграмма, используется для визуализации иерархических данных, изображаемых концентрическими кругами. [19] Круг в центре представляет корневой узел, а иерархия движется наружу от центра. Сегмент внутреннего круга имеет иерархическую связь с теми сегментами внешнего круга, которые лежат в пределах углового охвата родительского сегмента. [20]

Круговая диаграмма

Круговая диаграмма, сравнивающая количество студентов с расходами на обучение в четырех разных школах

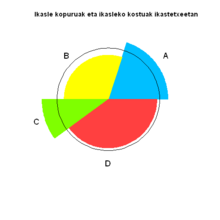
Вариантом полярной диаграммы является круговая диаграмма, разработанная Дрором Фейтельсоном. [21] Конструкция накладывает обычную круговую диаграмму на модифицированную полярную диаграмму, чтобы позволить сравнивать два набора связанных данных. Базовая круговая диаграмма представляет первый набор данных обычным способом с разными размерами срезов. Второй набор представлен наложенной полярной диаграммой с использованием тех же углов, что и у основания, и корректировкой радиусов для соответствия данным. Например, базовая круговая диаграмма может показывать распределение возрастных и гендерных групп в популяции и накладывать их представительство среди жертв дорожно-транспортных происшествий. Возрастные и гендерные группы, которые особенно подвержены попаданию в аварии, затем выделяются в виде срезов, которые выходят за пределы исходной круговой диаграммы.

Квадратная диаграмма / Вафельная диаграмма

Квадратная круговая диаграмма (вафельная диаграмма), показывающая, как меньшие проценты легче показать, чем на круговых диаграммах. На сетке 10x10 каждая ячейка представляет 1%.

Квадратные диаграммы, также называемые вафельными диаграммами, являются формой круговых диаграмм, которые используют квадраты вместо кругов для представления процентов. Подобно базовым круговым круговым диаграммам, квадратные круговые диаграммы берут каждый процент из общих 100%. Они часто представляют собой сетки 10 на 10, где каждая ячейка представляет 1%. Несмотря на название, вместо квадратов могут использоваться круги, пиктограммы (например, людей) и другие фигуры. Одним из главных преимуществ квадратных диаграмм является то, что можно легко изобразить меньшие проценты, которые трудно увидеть на традиционных круговых диаграммах. [22]

Пример

Круговая диаграмма для примера данных

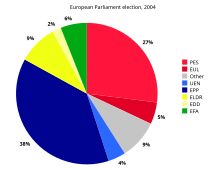
Следующий пример диаграммы основан на предварительных результатах выборов в Европейский парламент в 2004 году . В таблице указано количество мест, выделенных каждой партийной группе, а также полученный процент от общего числа, который каждая из них составляет. Значения в последнем столбце, полученный центральный угол каждого сектора, определяются путем взятия этого процента от 360.

*Из-за округления эти суммы не составляют в сумме 100 и 360.

Размер каждого центрального угла пропорционален размеру соответствующей величины, в данном случае количеству мест. Поскольку сумма центральных углов должна быть 360°, центральный угол для величины, которая является дробью Q от общей суммы, составляет 360 Q градусов. В примере центральный угол для самой большой группы (Европейская народная партия (EPP)) составляет 135,7°, поскольку 0,377 умножить на 360, округлив до одного десятичного знака, равно 135,7.

Использование и эффективность

Трехмерная круговая диаграмма, показывающая процентное содержание компонентов атмосферного воздуха

Недостаток круговых диаграмм заключается в том, что они не могут отображать больше нескольких значений, не отделяя визуальное кодирование («срезы») от данных, которые они представляют (обычно проценты). Когда срезы становятся слишком маленькими, круговым диаграммам приходится полагаться на цвета, текстуры или стрелки, чтобы читатель мог их понять. Это делает их непригодными для использования с большими объемами данных. Круговые диаграммы также занимают больше места на странице по сравнению с более гибкими столбчатыми диаграммами, которым не нужны отдельные легенды, и которые могут отображать другие значения, такие как средние или целевые значения, в то же время. [7]

Статистики обычно считают круговые диаграммы плохим методом отображения информации, и они нечасто встречаются в научной литературе. Одна из причин заключается в том, что сложнее проводить сравнения между размерами элементов на диаграмме, когда вместо длины используется площадь и когда разные элементы показаны в виде разных форм. [23]

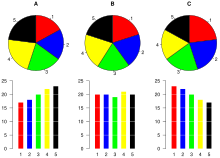
Три набора процентов, представленных как в виде круговых диаграмм, так и в виде столбчатых диаграмм. Сравнивать данные на столбчатых диаграммах обычно проще.

Кроме того, в исследовании, проведенном в AT&T Bell Laboratories , было показано, что сравнение по углу было менее точным, чем сравнение по длине. Большинство испытуемых испытывают трудности с упорядочиванием срезов в круговой диаграмме по размеру; при использовании эквивалентной столбчатой ​​диаграммы сравнение становится намного проще. [24] Аналогично, сравнения между наборами данных проще проводить с помощью столбчатой ​​диаграммы. Однако, если цель состоит в том, чтобы сравнить заданную категорию (срез пирога) с общим (весь пирог) в одной диаграмме, а кратное близко к 25 или 50 процентам, то круговая диаграмма часто может быть более эффективной, чем столбчатая диаграмма. [25] [26]

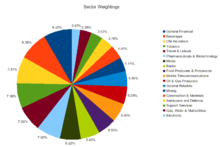
Пример круговой диаграммы с 18 значениями, в которой некоторые цвета повторяются

В круговой диаграмме с большим количеством секций несколько значений могут быть представлены одинаковыми или похожими цветами, что затрудняет интерпретацию.

Пример круговой диаграммы в форме пончика, показывающей результаты отбивания и пробежек индийских игроков в крикет в тестовых матчах в 2019 году.

Несколько исследований, представленных на Европейской конференции по визуализации, проанализировали относительную точность нескольких форматов круговых диаграмм, [27] [28] [22] придя к выводу, что круговые и кольцевые диаграммы дают схожие уровни ошибок при их чтении, а квадратные круговые диаграммы обеспечивают наиболее точное чтение. [29]

Смотрите также

Ссылки

  1. ^ abc Спенс (2005)
  2. ^ ab Tufte, стр. 44
  3. ^ Кливленд, стр. 262
  4. ↑ Уилкинсон, стр. 23.
  5. ↑ Тафти, стр. 178.
  6. ^ Ван Белль, стр. 160–162.
  7. ^ abc Stephen Few. «Save the Pies for Dessert», август 2007 г., дата обращения 2010-02-02
  8. ^ Стив Фентон «Круговые диаграммы — это плохо»
  9. ^ «Вехи в истории тематической картографии, статистической графики и визуализации данных». www.datavis.ca .
  10. ^ Палски, стр. 144–145
  11. ^ ab Гринбаум, Хилари; Рубинштейн, Дана (20 апреля 2012 г.). «Кто сделал эту круговую диаграмму?». The New York Times .
  12. ^ Статья Дэйва об этой информации на QI
  13. ^ Коэн, И. Бернард (март 1984 г.). «Флоренс Найтингейл». Scientific American . 250 (3): 128–137. Bibcode : 1984SciAm.250c.128C. doi : 10.1038/scientificamerican0384-128. PMID  6367033.(альтернативная нумерация страниц в зависимости от страны продажи: 98–107, библиография на стр. 114) онлайн-статья – см. ссылку на документы слева
  14. ↑ Гуд и Хардин, глава 8.
  15. ^ Харрис, Роберт Л. (1999). Информационная графика: полный иллюстрированный справочник ([Nachdr.] ред.). Оксфорд: Oxford University Press. стр. 143. ISBN 9780195135329.
  16. ^ ab Data Design Юргена Кай-Уве Брока на iBooks . Получено 10 июня 2017 г. {{cite book}}: |website=проигнорировано ( помощь )
  17. ^ Дружелюбный, стр. 509
  18. ^ "Статистические диаграммы Флоренс Найтингейл" . Получено 22.11.2010 .
  19. ^ "Многоуровневые круговые диаграммы". www.neoformix.com .
  20. ^ Веббер Ричард, Герберт Рик, Цзянбк Уэл. «Методы заполнения пространства при визуализации результатов компьютерных экономических моделей»
  21. ^ "Фейтельсон, Дрор (2003) Сравнение разделов с круговыми диаграммами" (PDF) . 2003 . Получено 31 августа 2010 г.
  22. ^ Аб Косара, Роберт; Скау, Дрю (2016). «Ошибка суждения в вариантах круговой диаграммы». ЕвроВис .
  23. ^ Крайгер, Джон (28 августа 2007 г.). «Перцептивное масштабирование символов карты». makingmaps.net . Получено 3 мая 2015 г. .
  24. ↑ Кливленд, стр. 86–87.
  25. ^ Симкин, Д. и Хасти, Р. (1987). Анализ обработки информации при восприятии графа. Журнал Американской статистической ассоциации, 82(398), 454. doi :10.2307/2289447. Косара, Роберт (13 апреля 2011 г.). "В защиту круговых диаграмм" . Получено 13 апреля 2011 г.
  26. ^ Спенс, Ян; Левандовски, Стефан (1 января 1991 г.). «Отображение пропорций и процентов». Прикладная когнитивная психология . 5 (1): 61–77. doi :10.1002/acp.2350050106.
  27. ^ "Иллюстрированный обзор результатов исследования круговой диаграммы". eatereyes . 2016-06-28 . Получено 2016-11-28 .
  28. ^ Скау, Дрю; Косара, Роберт (2016). «Дуги, углы или области: индивидуальные кодировки данных в круговых и кольцевых диаграммах». EuroVis .
  29. ^ "Повторный анализ исследования о (квадратных) круговых диаграммах от 2009 года". eatereyes . 2016-07-11 . Получено 2016-11-28 .

Дальнейшее чтение

Внешние ссылки

На Викискладе есть медиафайлы по теме Круговые диаграммы .