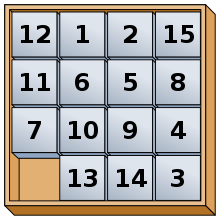
Головоломка 15 (также называемая Gem Puzzle , Boss Puzzle , Game of Fifteen , Mystic Square и т. д.) — это скользящая головоломка . Она состоит из 15 квадратных плиток, пронумерованных от 1 до 15, в рамке, которая имеет высоту и ширину 4 плитки, с одной незанятой позицией. Плитки в одном ряду или столбце открытой позиции можно перемещать, сдвигая их по горизонтали или вертикали соответственно. Цель головоломки — разместить плитки в числовом порядке (слева направо, сверху вниз).
Названная по количеству плиток в рамке, головоломка 15 может также называться «головоломкой 16» , намекая на ее общую емкость плиток. Похожие названия используются для различных вариантов головоломки 15, таких как головоломка 8, которая имеет 8 плиток в рамке 3×3.
Головоломка n является классической проблемой для моделирования алгоритмов, включающих эвристики . Обычно используемые эвристики для этой проблемы включают подсчет количества неправильно размещенных плиток и нахождение суммы расстояний такси между каждым блоком и его положением в целевой конфигурации. [1] Обратите внимание, что оба являются допустимыми . То есть они никогда не переоценивают количество оставшихся ходов, что обеспечивает оптимальность для определенных алгоритмов поиска , таких как A* . [1]

Джонсон и Стори (1879) использовали аргумент четности , чтобы показать, что половина начальных позиций для головоломки n неразрешимы, независимо от того, сколько ходов сделано. Это делается путем рассмотрения бинарной функции конфигурации плитки, которая инвариантна при любом допустимом ходе, а затем ее использования для разбиения пространства всех возможных помеченных состояний на два взаимно недоступных класса эквивалентности одинакового размера. Это означает, что половина всех позиций неразрешимы, хотя это ничего не говорит об оставшейся половине.
Инвариант — это четность перестановки всех 16 квадратов плюс четность расстояния такси (количество строк плюс количество столбцов) пустого квадрата из нижнего правого угла. Это инвариант, потому что каждый ход изменяет как четность перестановки, так и четность расстояния такси. В частности, если пустой квадрат находится в нижнем правом углу, то головоломка разрешима только в том случае, если перестановка оставшихся частей четная.
Джонсон и Стори (1879) также показали, что на досках размера m × n , где m и n оба больше или равны 2, все четные перестановки разрешимы . Это можно доказать индукцией по m и n , начиная с m = n = 2. Это означает, что существует ровно два класса эквивалентности взаимно доступных расположений, и что описанная четность является единственным нетривиальным инвариантом, хотя существуют эквивалентные описания.
Арчер (1999) дал другое доказательство, основанное на определении классов эквивалентности через гамильтонов путь .
Уилсон (1974) изучал обобщение головоломки 15 на произвольные конечные графы , причем исходная задача была случаем графа сетки 4×4 . У задачи есть несколько вырожденных случаев, когда ответ либо тривиален, либо является простой комбинацией ответов на ту же задачу на некоторых подграфах. А именно, для путей и многоугольников головоломка не имеет свободы; если граф несвязен , то имеет значение только связный компонент вершины с «пустым пространством»; и если есть вершина сочленения , задача сводится к той же задаче на каждом из двусвязных компонентов этой вершины. Исключая эти случаи, Уилсон показал, что, за исключением одного исключительного графа на 7 вершинах, можно получить все перестановки, если только граф не является двудольным , в этом случае можно получить ровно четные перестановки. Исключительный граф представляет собой правильный шестиугольник с одной диагональю и добавленной вершиной в центре; только 1/6 его перестановок может быть достигнуто, что дает пример экзотического вложения S 5 в S 6 .
Для больших версий головоломки n найти решение легко. Но задача поиска кратчайшего решения является NP-трудной . Также NP-трудно аппроксимировать наименьшее количество слайдов в пределах аддитивной константы, но существует аппроксимация полиномиального времени с постоянным множителем. [2] [3] Для головоломки 15 длина оптимальных решений варьируется от 0 до 80 ходов одной плитки (существует 17 конфигураций, требующих 80 ходов) [4] [5] или 43 хода нескольких плиток; [6] головоломка 8 всегда может быть решена не более чем за 31 ход одной плитки или 24 хода нескольких плиток (целая последовательность A087725). Метрика нескольких плиток учитывает последующие ходы пустой плитки в том же направлении как один. [6]
Число возможных положений головоломки 24 равно 25!/2 ≈7,76 × 10 24 , что слишком много, чтобы вычислить число Бога с помощью методов грубой силы. В 2011 году были установлены нижние границы в 152 хода одной плитки или 41 ход нескольких плиток, а также верхние границы в 208 ходов одной плитки или 109 ходов нескольких плиток. [7] [8] [9] [10] В 2016 году верхняя граница была улучшена до 205 ходов одной плитки. [11]
Преобразования головоломки 15 образуют группоид (не группу, поскольку не все ходы могут быть составлены); [12] [13] [14] этот группоид действует на конфигурации.
Поскольку комбинации головоломки из 15 могут быть получены с помощью 3-циклов , можно доказать, что головоломка из 15 может быть представлена чередующейся группой . [15] Фактически, любая раздвижная головоломка с квадратными плитками одинакового размера может быть представлена как .


Головоломка была «изобретена» Нойесом Палмером Чепменом [16], почтмейстером в Канастоте, штат Нью-Йорк , который, как говорят, показал друзьям еще в 1874 году предшественника головоломки, состоящего из 16 пронумерованных блоков, которые нужно было сложить в ряды по четыре, каждый из которых в сумме давал 34 (см. магический квадрат ). Копии улучшенной головоломки 15 попали в Сиракузы, штат Нью-Йорк , через сына Чепмена, Фрэнка, а оттуда, через различные связи, в Уотч-Хилл, Род-Айленд , и, наконец, в Хартфорд , Коннектикут , где ученики Американской школы для глухих начали изготавливать головоломку. К декабрю 1879 года они продавались как на местном уровне, так и в Бостоне , штат Массачусетс . Показав одну из них, Маттиас Райс, который управлял деревообрабатывающим бизнесом в Бостоне, начал производить головоломку где-то в декабре 1879 года и убедил торговца галантерейными товарами «Yankee Notions» продавать их под названием «Gem Puzzle». В конце января 1880 года Чарльз Пиви, дантист из Вустера , штат Массачусетс, привлек некоторое внимание, предложив денежное вознаграждение за решение головоломки 15. [16]
Игра стала модной в США в 1880 году. [17]
Чепмен подал заявку на патент на свою «Головоломку-пасьянс из блоков» 21 февраля 1880 года. Однако этот патент был отклонен, вероятно, потому, что он недостаточно отличался от патента «Головоломки-блоки» от 20 августа 1878 года (US 207124), выданного Эрнесту У. Кинси. [16]

С 1891 года и до своей смерти в 1911 году Сэм Лойд утверждал, что он изобрёл головоломку. Однако Лойд не имел никакого отношения к изобретению или первоначальной популярности головоломки. Первая статья Лойда о головоломке была опубликована в 1886 году, и только в 1891 году он впервые заявил, что является изобретателем. [16] [18]
Более поздний интерес был подогрет предложением Лойда премии в размере 1000 долларов США (что эквивалентно 33 911 долларам США в 2023 году) любому, кто сможет предоставить решение для достижения определенной комбинации, указанной Лойдом, а именно, поменять местами 14 и 15, что Лойд назвал головоломкой 14-15 . [1] Это невозможно, как было показано более чем десятилетием ранее Джонсоном и Стори (1879), поскольку для этого требуется преобразование из четной перестановки в нечетную.
Кубик «Минус» , произведенный в СССР , представляет собой 3D- головоломку с операциями, аналогичными головоломке «15».
Версии головоломки «15» включают в себя разное количество плиток, например, головоломка «8» или «24».
Чемпион мира по шахматам Бобби Фишер был экспертом в решении головоломки «15». [19] Он должен был решить ее за 25 секунд; Фишер продемонстрировал это 8 ноября 1972 года в программе «The Tonight Show Starring Johnny Carson» . [20] [21]