Граница зерна

Интерфейс между кристаллитами в поликристаллическом материале

Микрофотография поликристаллического металла ; границы зерен выявлены с помощью кислотного травления.

Различно ориентированные кристаллиты в поликристаллическом материале

В материаловедении граница зерен — это интерфейс между двумя зернами или кристаллитами в поликристаллическом материале. Границы зерен — это двумерные дефекты в кристаллической структуре , которые имеют тенденцию снижать электро- и теплопроводность материала. Большинство границ зерен являются предпочтительными местами для начала коррозии ^[1] и для осаждения новых фаз из твердого тела. Они также важны для многих механизмов ползучести ^[2] . С другой стороны, границы зерен нарушают движение дислокаций через материал, поэтому уменьшение размера кристаллитов является распространенным способом повышения механической прочности, как описано соотношением Холла-Петча .

Границы высокого и низкого угла

Границы зерен удобно классифицировать в соответствии со степенью разориентации между двумя зернами. Малоугловые границы зерен ( LAGB ) или субзеренные границы - это те, у которых разориентация составляет менее 15 градусов. ^[3] В общем, они состоят из массива дислокаций , а их свойства и структура являются функцией разориентации. Напротив, свойства большеугловых границ зерен , разориентация которых составляет более 15 градусов (угол перехода варьируется от 10 до 15 градусов в зависимости от материала), обычно не зависят от разориентации. Однако существуют «особые границы» в определенных ориентациях, интерфейсные энергии которых заметно ниже, чем у общих большеугловых границ зерен.

Схематические изображения границы наклона (вверху) и границы кручения между двумя идеализированными зернами.

Простейшей границей является граница наклона, где ось вращения параллельна плоскости границы. Эту границу можно представить как формирующуюся из одного, смежного кристаллита или зерна, которое постепенно изгибается некоторой внешней силой. Энергию, связанную с упругим изгибом решетки, можно уменьшить, вставив дислокацию, которая по сути является полуплоскостью атомов, действующих как клин, который создает постоянную разориентацию между двумя сторонами. По мере того, как зерно изгибается дальше, все больше и больше дислокаций должно быть введено, чтобы приспособиться к деформации, приводящей к растущей стенке дислокаций – малоугловой границе. Теперь можно считать, что зерно разделилось на два субзерна со связанной кристаллографией, но заметно отличающейся ориентацией.

Альтернативой является граница кручения, где разориентация происходит вокруг оси, перпендикулярной плоскости границы. Этот тип границы включает два набора винтовых дислокаций . Если векторы Бюргерса дислокаций ортогональны, то дислокации не сильно взаимодействуют и образуют квадратную сетку. В других случаях дислокации могут взаимодействовать, образуя более сложную гексагональную структуру.

Эти концепции наклонных и крутильных границ представляют собой несколько идеализированные случаи. Большинство границ являются смешанными, содержащими дислокации разных типов и векторы Бюргерса, чтобы создать наилучшее соответствие между соседними зернами.

Если дислокации на границе остаются изолированными и четкими, границу можно считать малоугловой. Если деформация продолжается, плотность дислокаций увеличится и, таким образом, уменьшит расстояние между соседними дислокациями. В конце концов, ядра дислокаций начнут перекрываться, и упорядоченная природа границы начнет разрушаться. В этот момент границу можно считать высокоугловой, а исходное зерно разделилось на два совершенно отдельных зерна.

По сравнению с границами зерен с малыми углами, границы с большими углами значительно более неупорядочены, с большими областями плохого соответствия и сравнительно открытой структурой. Действительно, изначально считалось, что они представляют собой некоторую форму аморфного или даже жидкого слоя между зернами. Однако эта модель не могла объяснить наблюдаемую прочность границ зерен, и после изобретения электронной микроскопии прямые доказательства структуры зерен означали, что гипотезу пришлось отбросить. В настоящее время принято считать, что граница состоит из структурных единиц, которые зависят как от разориентации двух зерен, так и от плоскости интерфейса. Типы существующих структурных единиц могут быть связаны с концепцией решетки совпадающих узлов , в которой повторяющиеся единицы образуются из точек, где два совпадающих узла \ В теории решетки совпадающих узлов (CSL) степень соответствия (Σ) между структурами двух зерен описывается обратной величиной отношения числа узлов совпадения к общему числу узлов. ^[4]

В этой структуре можно нарисовать решетку для двух зерен и подсчитать количество атомов, которые являются общими (места совпадения), и общее количество атомов на границе (общее количество мест). Например, когда Σ=3, будет один атом из каждых трех, который будет общим между двумя решетками. Таким образом, можно ожидать, что граница с высоким Σ будет иметь более высокую энергию, чем граница с низким Σ. Малоугловые границы, где искажение полностью компенсируется дислокациями, являются Σ1. Некоторые другие границы с низким Σ обладают особыми свойствами, особенно когда плоскость границы является той, которая содержит высокую плотность совпадающих мест. Примерами являются когерентные границы двойников (например, Σ3) и границы с высокой подвижностью в материалах ГЦК (например, Σ7). Отклонения от идеальной ориентации CSL могут быть компенсированы локальной атомной релаксацией или включением дислокаций на границе.

Описание границы

Граница может быть описана ориентацией границы к двум зернам и 3-D вращением, необходимым для приведения зерен в совпадение. Таким образом, граница имеет 5 макроскопических степеней свободы . Однако принято описывать границу только как ориентационное отношение соседних зерен. Как правило, удобство игнорирования ориентации плоскости границы, которую очень трудно определить, перевешивает сокращенную информацию. Относительная ориентация двух зерен описывается с помощью матрицы вращения :

Характерное распределение граничных разориентаций в совершенно случайно ориентированном наборе зерен для материалов с кубической симметрией.

${\displaystyle R={\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}}}$

Используя эту систему, угол поворота θ равен:

${\displaystyle 2\cos \;\theta \;+1=a_{11}+a_{22}+a_{33}\,\!}$

в то время как направление [uvw] оси вращения равно:

${\displaystyle [(a_{32}-a_{23}),(a_{13}-a_{31}),(a_{21}-a_{12})]\,\!}$

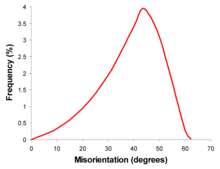
Природа кристаллографии ограничивает разориентацию границы. Полностью случайный поликристалл без текстуры, таким образом, имеет характерное распределение разориентаций границы (см. рисунок). Однако такие случаи редки, и большинство материалов будут отклоняться от этого идеала в большей или меньшей степени.

Граничная энергия

Энергия наклонной границы и энергия на дислокацию по мере увеличения разориентации границы

Энергия малоугловой границы зависит от степени разориентации между соседними зернами вплоть до перехода в состояние с большим углом. В случае простых наклонных границ энергия границы, состоящей из дислокаций с вектором Бюргерса b и расстоянием h, предсказывается уравнением Рида–Шокли :

${\displaystyle \gamma _{s}=\gamma _{0}\theta (A-\ln \theta )\,\!}$

где:

${\displaystyle \theta =b/h\,\!}$

${\displaystyle \gamma _{0}=Gb/4\pi (1-\nu )\,\!}$

${\displaystyle A=1+\ln(b/2\pi r_{0})\,\!}$

где - модуль сдвига , - коэффициент Пуассона , а - радиус ядра дислокации. Видно, что по мере увеличения энергии границы энергия на дислокацию уменьшается. Таким образом, существует движущая сила, которая приводит к образованию меньшего количества разориентированных границ (т. е. росту зерна ). ${\displaystyle G}$ ${\displaystyle \nu }$ ${\displaystyle r_{0}}$

Ситуация в высокоугловых границах более сложная. Хотя теория предсказывает, что энергия будет минимальной для идеальных конфигураций CSL, с отклонениями, требующими дислокаций и других энергетических характеристик, эмпирические измерения показывают, что связь более сложная. Некоторые предсказанные провалы в энергии обнаружены, как и ожидалось, в то время как другие отсутствуют или существенно уменьшены. Обзоры имеющихся экспериментальных данных показали, что простые связи, такие как низкая, вводят в заблуждение: ${\displaystyle \Sigma }$

Сделан вывод, что ни один общий и полезный критерий низкой энергии не может быть закреплен в простой геометрической структуре. Любое понимание изменений межфазной энергии должно учитывать атомную структуру и детали связи на интерфейсе. ^[5]

Избыточный объем

Избыточный объем является еще одним важным свойством в характеристике границ зерен. Избыточный объем был впервые предложен Бишопом в частном сообщении Аарону и Боллингу в 1972 году. ^[6] Он описывает, насколько сильно расширение вызвано наличием ГЗ, и считается, что степень и восприимчивость к сегрегации прямо пропорциональны этому. Несмотря на название, избыточный объем на самом деле является изменением длины, это происходит из-за двумерной природы ГЗ, длина интереса - это расширение, нормальное к плоскости ГЗ. Избыточный объем ( ) определяется следующим образом: ${\displaystyle \delta V}$

${\displaystyle \delta V=\left({\frac {\partial V}{\partial A}}\right)_{T,p,n_{i}},}$

при постоянной температуре , давлении и числе атомов . Хотя существует грубая линейная зависимость между энергией ГБ и избыточным объемом, ориентации, в которых эта зависимость нарушается, могут вести себя существенно по-разному, влияя на механические и электрические свойства. ^[7] ${\displaystyle T}$ ${\displaystyle p}$ ${\displaystyle n_{i}}$

Были разработаны экспериментальные методы, которые напрямую исследуют избыточный объем и использовались для исследования свойств нанокристаллической меди и никеля . ^{[8] [9]} Теоретические методы также были разработаны ^[10] и находятся в хорошем согласии. Ключевое наблюдение заключается в том, что существует обратная зависимость с модулем объемной упругости, что означает, что чем больше модуль объемной упругости (способность сжимать материал), тем меньше будет избыточный объем, также существует прямая связь с постоянной решетки, это обеспечивает методологию для поиска материалов с желаемым избыточным объемом для конкретного применения.

Пограничная миграция

Движение границ зерен (HAGB) оказывает влияние на рекристаллизацию и рост зерен, в то время как движение границ субзерен (LAGB) сильно влияет на восстановление и зарождение рекристаллизации.

Граница движется из-за давления, действующего на нее. Обычно предполагается, что скорость прямо пропорциональна давлению, а константа пропорциональности — подвижности границы. Подвижность сильно зависит от температуры и часто следует соотношению типа Аррениуса :

${\displaystyle M=M_{0}\exp \left(-{\frac {Q}{RT}}\right)\,\!}$

Кажущаяся энергия активации (Q) может быть связана с термически активированными атомистическими процессами, которые происходят во время движения границы. Однако существует несколько предложенных механизмов, где подвижность будет зависеть от движущего давления, и предполагаемая пропорциональность может нарушиться.

Общепринято, что подвижность малоугловых границ намного ниже, чем у высокоугловых границ. Следующие наблюдения, по-видимому, справедливы для ряда условий:

• Подвижность малоугловых границ пропорциональна действующему на них давлению.
• Процесс регулирования скорости - это процесс объемной диффузии.
• Подвижность границ увеличивается с дезориентацией.

Поскольку границы с малым углом состоят из массивов дислокаций, и их движение может быть связано с теорией дислокаций. Наиболее вероятным механизмом, учитывая экспериментальные данные, является механизм переползания дислокаций, скорость которого ограничена диффузией растворенного вещества в объеме. ^[11]

Перемещение высокоугловых границ происходит путем переноса атомов между соседними зернами. Легкость, с которой это может произойти, будет зависеть от структуры границы, которая сама зависит от кристаллографии вовлеченных зерен, примесных атомов и температуры. Возможно, что некоторая форма бездиффузионного механизма (сродни бездиффузионным фазовым превращениям, таким как мартенсит ) может работать в определенных условиях. Некоторые дефекты на границе, такие как ступеньки и выступы, также могут предлагать альтернативные механизмы для атомного переноса.

Рост зерна может быть подавлен частицами второй фазы посредством закрепления по методу Ценера .

Поскольку граница с большим углом упакована неидеально по сравнению с нормальной решеткой, она имеет некоторое количество свободного пространства или свободного объема , где атомы растворенного вещества могут обладать более низкой энергией. В результате граница может быть связана с атмосферой растворенного вещества , которая будет замедлять ее движение. Только при более высоких скоростях граница сможет вырваться из своей атмосферы и возобновить нормальное движение.

Как низко-, так и высокоугловые границы замедляются присутствием частиц через так называемый эффект закрепления Зенера . Этот эффект часто используется в коммерческих сплавах для минимизации или предотвращения рекристаллизации или роста зерен во время термообработки .

Цвет лица

Границы зерен являются предпочтительным местом сегрегации примесей, которые могут образовывать тонкий слой с составом, отличным от основного объема, и разнообразными атомными структурами, отличными от прилегающих кристаллических фаз. Например, тонкий слой кремния, который также содержит примесные катионы, часто присутствует в нитриде кремния.

Граничные комплексы зерен были введены Минг Таном, Роулендом Кэнноном и У. Крейгом Картером в 2006 году. ^[12]

Эти фазы границ зерен термодинамически стабильны и могут рассматриваться как квазидвумерная фаза, которая может подвергаться переходу, подобно фазам объемных фаз. В этом случае возможны резкие изменения структуры и химии при критическом значении термодинамического параметра, такого как температура или давление. ^[13] Это может сильно повлиять на макроскопические свойства материала, например, на электрическое сопротивление или скорость ползучести. ^[14] Границы зерен можно проанализировать с помощью равновесной термодинамики, но их нельзя рассматривать как фазы, поскольку они не удовлетворяют определению Гиббса: они неоднородны, могут иметь градиент структуры, состава или свойств. По этой причине их определяют как комплексион: интерфейсный материал или состояние, который находится в термодинамическом равновесии со своими примыкающими фазами, с конечной и стабильной толщиной (обычно 2–20 Å). Для существования комплексиона необходима примыкающая фаза, а его состав и структура должны отличаться от примыкающей фазы. В отличие от объемных фаз, комплексионы также зависят от примыкающей фазы. Например, аморфный слой, богатый кремнием, присутствующий в Si ₃ N ₃ , имеет толщину около 10 Å, но для особых границ эта равновесная толщина равна нулю. ^[15] Комплексообразование можно сгруппировать в 6 категорий в соответствии с их толщиной: монослой, бислой, трислой, нанослой (с равновесной толщиной от 1 до 2 нм) и смачивание. В первых случаях толщина слоя будет постоянной; если присутствует дополнительный материал, он будет сегрегировать на множественном стыке зерен, тогда как в последнем случае равновесной толщины нет, и это определяется количеством вторичной фазы, присутствующей в материале. Одним из примеров перехода комплексообразующего состояния границ зерен является переход от сухой границы к двухслойному в Si, легированном золотом, который производится увеличением золота. ^[16]

Влияние на электронную структуру

Границы зерен могут вызывать механические разрушения из-за охрупчивания через сегрегацию растворенного вещества (см. Атомная электростанция Хинкли-Пойнт А ), но они также могут пагубно влиять на электронные свойства. В оксидах металлов было теоретически показано, что на границах зерен в Al ₂ O ₃ и MgO изолирующие свойства могут быть значительно снижены. ^[17] Используя теорию функционала плотности, компьютерное моделирование границ зерен показало, что ширина запрещенной зоны может быть уменьшена до 45%. ^[18] В случае металлов границы зерен увеличивают удельное сопротивление, поскольку размер зерен относительно средней длины свободного пробега других рассеивателей становится значительным. ^[19]

Концентрация дефектов вблизи границ зерен

Известно, что большинство материалов являются поликристаллическими и содержат границы зерен, и что границы зерен могут действовать как стоки и пути транспортировки точечных дефектов. Однако экспериментально и теоретически определить, какое влияние точечные дефекты оказывают на систему, сложно. ^{[20] [21] [22]} Интересные примеры осложнений поведения точечных дефектов проявились в температурной зависимости эффекта Зеебека. ^[23] Кроме того, диэлектрический и пьезоэлектрический отклик может быть изменен распределением точечных дефектов вблизи границ зерен. ^[24] Механические свойства также могут существенно зависеть от таких свойств, как объемный модуль упругости и затухание, на которые влияют изменения распределения точечных дефектов внутри материала. ^{[25] [26]} Также было обнаружено, что эффект Кондо в графене можно настроить из-за сложной взаимосвязи между границами зерен и точечными дефектами. ^[27] Недавние теоретические расчеты показали, что точечные дефекты могут быть чрезвычайно благоприятными вблизи определенных типов границ зерен и существенно влиять на электронные свойства с уменьшением ширины запрещенной зоны. ^[28]

Связь между теорией и экспериментом

Было проведено значительное количество экспериментальной работы по наблюдению как структуры, так и измерения свойств границ зерен, но пятимерные степени свободы границ зерен в сложных поликристаллических сетях еще не полностью изучены, и поэтому в настоящее время не существует метода управления структурой и свойствами большинства металлов и сплавов с атомной точностью. ^[29] Часть проблемы связана с тем фактом, что большая часть теоретической работы по пониманию границ зерен основана на построении бикристаллических (двух) зерен, которые не представляют собой сеть зерен, обычно встречающуюся в реальной системе, а использование классических силовых полей, таких как метод внедренного атома, часто не описывает физику вблизи зерен правильно, и для получения реалистичных представлений может потребоваться теория функционала плотности . Точное моделирование границ зерен как с точки зрения структуры, так и с точки зрения атомных взаимодействий может иметь эффект улучшения проектирования, что может сократить отходы и повысить эффективность с точки зрения использования материала и производительности. С вычислительной точки зрения большая часть исследований границ зерен была сосредоточена на бикристаллических системах, это системы, которые рассматривают только две границы зерен. Недавно была проведена работа, в которой использовались новые модели эволюции зерен, показывающие, что существуют существенные различия в свойствах материалов, связанные с наличием изогнутых или плоских зерен. ^[30]

Смотрите также

• Аномальный рост зерна
• Разделение материалов

Ссылки

1. Lehockey, EM; Palumbo, G.; Lin, P.; Brennenstuhl, AM (май 1997). «О связи между распределением характера границ зерен и межкристаллитной коррозией». Scripta Materialia . 36 (10): 1211–1218. doi :10.1016/S1359-6462(97)00018-3.
2. Радж, Р.; Эшби, М.Ф. (апрель 1971 г.). «О скольжении по границам зерен и диффузионной ползучести». Metallurgical Transactions . 2 (4): 1113–1127. Bibcode :1971MT......2.1113R. doi :10.1007/BF02664244.
3. Готтштейн, Гюнтер (2004). Физические основы материаловедения . doi :10.1007/978-3-662-09291-0. ISBN 978-3-642-07271-0.^{[ нужна страница ]}
4. Гриммер, Х.; Боллманн, В.; Уоррингтон, Д.Х. (март 1974 г.). «Решетки совпадающих узлов и полный сдвиг структуры в кубических кристаллах». Acta Crystallographica Section A. 30 ( 2): 197–207. Bibcode : 1974AcCrA..30..197G. doi : 10.1107/S056773947400043X.
5. Sutton, AP; Balluffi, RW (сентябрь 1987 г.). «Обзор № 61 о геометрических критериях низкой межфазной энергии». Acta Metallurgica . 35 (9): 2177–2201. doi :10.1016/0001-6160(87)90067-8.
6. Аарон, Х. Б.; Боллинг, Г. Ф. (1972). «Свободный объем как критерий для моделей границ зерен». Surface Science . 31 (C): 27–49. Bibcode :1972SurSc..31...27A. doi :10.1016/0039-6028(72)90252-X.
7. Вольф, Д. (1989). «Корреляция между энергией и расширением объема для границ зерен в металлах с ГЦК-решеткой». Scripta Metallurgica . 23 (11): 1913–1918. doi :10.1016/0036-9748(89)90482-1.
8. Стейскал, Ева-Мария; Обердорфер, Бернд; Шпренгель, Вольфганг; Зехетбауэр, Майкл; Пиппан, Рейнхард; Вюршум, Роланд (31 января 2012 г.). «Прямое экспериментальное определение избыточного объема границ зерен в металлах». Письма о физических отзывах . 108 (5): 055504. Бибкод : 2012PhRvL.108e5504S. doi : 10.1103/PhysRevLett.108.055504 . ПМИД  22400941.
9. Обердорфер, Бернд; Сетман, Дарья; Стейскал, Ева-Мария; Хоэнвартер, Антон; Шпренгель, Вольфганг; Зехетбауэр, Майкл; Пиппан, Рейнхард; Вюршум, Роланд (апрель 2014 г.). «Зернограничный избыточный объем и дефектный отжиг меди после кручения под высоким давлением». Акта Материалия . 68 (100): 189–195. Бибкод : 2014AcMat..68..189O. doi :10.1016/j.actamat.2013.12.036. ПМЦ 3990421 . ПМИД  24748848. 
10. Бин, Джонатан Дж.; Маккенна, Кит П. (май 2016 г.). «Происхождение различий в избыточном объеме границ зерен меди и никеля». Acta Materialia . 110 : 246–257. Bibcode : 2016AcMat.110..246B. doi : 10.1016/j.actamat.2016.02.040.
11. Хамфрис, Ф. Дж.; Хазерли, М. (2004). Рекристаллизация и связанные с ней явления отжига . doi : 10.1016/B978-0-08-044164-1.X5000-2. ISBN 978-0-08-044164-1.^{[ нужна страница ]}
12. Tang, Ming; Carter, W. Craig; Cannon, Rowland M. (14 августа 2006 г.). «Переходы границ зерен в бинарных сплавах». Physical Review Letters . 97 (7): 075502. Bibcode : 2006PhRvL..97g5502T. doi : 10.1103/PhysRevLett.97.075502. PMID  17026243.
13. Sutton, Adrian P.; Balluffi, RW (1995). Интерфейсы в кристаллических материалах . Clarendon Press. ISBN 978-0-19-851385-8. OCLC  31166519.^{[ нужна страница ]}
14. Харт, Эдвард В. (1972). «Фазовые превращения на границах зерен». Природа и поведение границ зерен . стр. 155–170. doi :10.1007/978-1-4757-0181-4_6. ISBN 978-1-4757-0183-8.
15. Кантвелл, Патрик Р.; Тан, Мин; Диллон, Шен Дж.; Ло, Цзянь; Рорер, Грегори С.; Хармер, Мартин П. (январь 2014 г.). «Комплексы границ зерен». Acta Materialia . 62 : 1–48. Bibcode : 2014AcMat..62....1C. doi : 10.1016/j.actamat.2013.07.037. DTIC ADA601364.
16. Ma, Shuailei; Meshinchi Asl, Kaveh; Tansarawiput, Chookiat; Cantwell, Patrick R.; Qi, Minghao; Harmer, Martin P.; Luo, Jian (март 2012 г.). «Фазовый переход на границе зерен в Si–Au». Scripta Materialia . 66 (5): 203–206. doi :10.1016/j.scriptamat.2011.10.011.
17. Гуль, Ханнес; Ли, Хак-Сунг; Тэнгни, Пол; Фулкс, WMC; Хойер, Артур Х.; Накагава, Цубаса; Икухара, Юичи; Финнис, Майкл В. (2015). «Структурные и электронные свойства границ зерен Σ7 в α-Al ₂ O ₃ ». Акта Материалия . 99 . Эльзевир Б.В.: 16–28. Бибкод : 2015AcMat..99...16G. doi :10.1016/j.actamat.2015.07.042. hdl : 10044/1/25490 . S2CID  94617212.
18. Bean, Jonathan J.; Saito, Mitsuhiro; Fukami, Shunsuke; Sato, Hideo; Ikeda, Shoji; Ohno, Hideo; Ikuhara, Yuichi; McKenna, Keith P. (4 апреля 2017 г.). "Атомная структура и электронные свойства границ зерен MgO в туннельных магниторезистивных устройствах". Scientific Reports . 7 (1): 45594. Bibcode :2017NatSR...745594B. doi :10.1038/srep45594. PMC 5379487 . PMID  28374755. 
19. Mayadas, AF; Shatzkes, M. (15 февраля 1970 г.). «Модель электрического сопротивления для поликристаллических пленок: случай произвольного отражения на внешних поверхностях». Physical Review B. 1 ( 4): 1382–1389. Bibcode : 1970PhRvB...1.1382M. doi : 10.1103/physrevb.1.1382.
20. МакКласки, MD; Джокела, SJ (2009). «Дефекты в ZnO». Журнал прикладной физики . 106 (7): 071101–071101–13. Bibcode : 2009JAP...106g1101M. doi : 10.1063/1.3216464. S2CID  122634653.
21. Мейер, Рене; Васер, Райнер; Гельмбольд, Джулия; Борхардт, Гюнтер (2003). «Наблюдение миграции дефектов вакансий в катионной подрешетке сложных оксидов с помощью¹⁸
    O Tracer Experiments". Physical Review Letters . 90 (10): 105901. Bibcode : 2003PhRvL..90j5901M. doi : 10.1103/PhysRevLett.90.105901. PMID  12689009. S2CID  11680149.
22. Uberuaga, Blas Pedro; Vernon, Louis J.; Martinez, Enrique; Voter, Arthur F. (2015). "Взаимосвязь между структурой границ зерен, подвижностью дефектов и эффективностью стока границ зерен". Scientific Reports . 5 : 9095. Bibcode :2015NatSR...5E9095U. doi :10.1038/srep09095. PMC 4357896 . PMID  25766999. 
23. Кишимото, Кенго; Цукамото, Масаёши; Коянаги, Цуёши (ноябрь 2002 г.). «Температурная зависимость коэффициента Зеебека и рассеяние потенциального барьера пленок PbTe n -типа, полученных на нагретых стеклянных подложках методом высокочастотного распыления». Журнал прикладной физики . 92 (9): 5331–5339. Bibcode : 2002JAP....92.5331K. doi : 10.1063/1.1512964.
24. Bassiri-Gharb, Nazanin; Fujii, Ichiro; Hong, Eunki; Trolier-Mckinstry, Susan; Taylor, David V.; Damjanovic, Dragan (2007). «Вклад доменных стенок в свойства пьезоэлектрических тонких пленок». Journal of Electroceramics . 19 : 49–67. doi :10.1007/s10832-007-9001-1. S2CID  137189236.
25. Данг, Хан К.; Спирот, Дуглас Э. (2014). «Влияние точечных и зернограничных дефектов на механическое поведение монослоя MoS2
    ₂под напряжением посредством атомистического моделирования». Журнал прикладной физики . 116 (1): 013508. Bibcode : 2014JAP...116a3508D. doi : 10.1063/1.4886183.
26. Чжан, Дж.; Перес, Р. Дж.; Лаверния, Э. Дж. (1993). «Демпфирование, вызванное дислокациями, в композитах с металлической матрицей». Журнал материаловедения . 28 (3): 835–846. Bibcode : 1993JMatS..28..835Z. doi : 10.1007/BF01151266. S2CID  137660500.
27. Чэнь, Цзянь-Хао; Ли, Лян; Каллен, Уильям Г.; Уильямс, Эллен Д.; Фюрер, Майкл С. (2011). «Настраиваемый эффект Кондо в графене с дефектами». Nature Physics . 7 (7): 535–538. arXiv : 1004.3373 . Bibcode :2011NatPh...7..535C. doi :10.1038/nphys1962. S2CID  119210230.
28. Бин, Джонатан Дж.; Маккенна, Кит П. (2018). "Устойчивость точечных дефектов вблизи границ зерен MgO в магнитных туннельных переходах FeCoB/MgO/FeCoB" (PDF) . Physical Review Materials . 2 (12): 125002. Bibcode :2018PhRvM...2l5002B. doi :10.1103/PhysRevMaterials.2.125002. S2CID  197631853.
29. Королев, В. В.; Бин, Дж. Дж. (2022). «Сравнение пятимерных и низкомерных характеристик границ зерен и распределений энергии в меди: эксперимент и моделирование молекулярной статики». Metall Mater Trans A. 54 ( 2): 449–459. Bibcode : 2022MMTA...53..449K. doi : 10.1007/s11661-021-06500-5. S2CID  245636012.
30. Форрест, Роберт М.; Лазар, Эмануэль А.; Гоэль, Саурав; Бин, Джонатан Дж. (5 декабря 2022 г.). «Количественная оценка различий в свойствах поликристаллов, содержащих плоские и изогнутые границы зерен». Нанофабрикация . 7 . doi :10.37819/nanofab.007.250.

Дальнейшее чтение

• Doherty, RD; Hughes, DA; Humphreys, FJ; Jonas, JJ; Jensen, D.Juul; Kassner, ME; King, WE; McNelley, TR; McQueen, HJ; Rollett, AD (ноябрь 1997 г.). «Текущие проблемы рекристаллизации: обзор». Materials Science and Engineering: A . 238 (2): 219–274. doi :10.1016/S0921-5093(97)00424-3. hdl : 10945/40175 . S2CID  17885466.
• Готтштейн, Гюнтер; Швиндлерман, Лазар С. (2009). Миграция границ зерен в металлах . doi :10.1201/9781420054361. ISBN 978-0-429-14738-8.