В теории групп , подполе абстрактной алгебры , граф циклов группы — это неориентированный граф , иллюстрирующий различные циклы этой группы, заданные набором генераторов для группы. Графы циклов особенно полезны для визуализации структуры небольших конечных групп .
Цикл — это набор степеней заданного элемента группы a , где a n , n -я степень элемента a , определяется как произведение a, умноженное на себя n раз. Говорят, что элемент a порождает цикл. В конечной группе некоторая ненулевая степень a должна быть групповым тождеством , которое мы обозначаем либо как e, либо как 1; наименьшая такая степень — это порядок элемента a , число различных элементов в цикле, который он порождает. В графе цикла цикл представлен в виде многоугольника, вершины которого представляют элементы группы, а ребра указывают, как они связаны друг с другом, образуя цикл.
Каждый элемент группы представлен узлом в графе цикла, и достаточное количество циклов представлено в виде полигонов в графе, так что каждый узел лежит по крайней мере на одном цикле. Все эти полигоны проходят через узел, представляющий идентичность, и некоторые другие узлы также могут лежать более чем на одном цикле.
Предположим, что элемент группы a генерирует цикл порядка 6 (имеет порядок 6), так что узлы a , a 2 , a 3 , a 4 , a 5 и a 6 = e являются вершинами шестиугольника в графе цикла. Элемент a 2 тогда имеет порядок 3; но если сделать узлы a 2 , a 4 и e вершинами треугольника в графе, это не добавит никакой новой информации. Поэтому нужно рассматривать только примитивные циклы, те, которые не являются подмножествами другого цикла. Кроме того, узел a 5 , который также имеет порядок 6, генерирует тот же цикл, что и сам a ; поэтому у нас есть по крайней мере два выбора для того, какой элемент использовать при генерации цикла, — часто больше.
Чтобы построить циклический граф для группы, мы начинаем с узла для каждого элемента группы. Затем для каждого примитивного цикла мы выбираем некоторый элемент a , который генерирует этот цикл, и соединяем узел для e с узлом для a , a с a 2 , ..., a k −1 с a k и т. д., пока не вернемся к e . Результатом является циклический граф для группы.
Когда элемент группы a имеет порядок 2 (так что умножение на a является инволюцией ), правило выше соединит e с a двумя ребрами, одно из которых выходит, а другое возвращается. За исключением случаев, когда намерение состоит в том, чтобы подчеркнуть два ребра такого цикла, он обычно рисуется [1] как одна линия между двумя элементами.
Обратите внимание, что это соответствие между группами и графами не является однозначным ни в одном направлении: две разные группы могут иметь один и тот же циклический граф, и два разных графа могут быть циклическими графами для одной группы. Мы приводим примеры каждого в разделе неуникальности.
В качестве примера графа группового цикла рассмотрим диэдральную группу Dih 4. Таблица умножения для этой группы показана слева, а граф цикла показан справа, где e указывает единичный элемент.
Обратите внимание на цикл { e , a , a 2 , a 3 } в таблице умножения, где a 4 = e . Обратный a −1 = a 3 также является генератором этого цикла: ( a 3 ) 2 = a 2 , ( a 3 ) 3 = a , и ( a 3 ) 4 = e . Аналогично, любой цикл в любой группе имеет по крайней мере два генератора и может быть пройден в любом направлении. В более общем смысле, количество генераторов цикла с n элементами задается функцией Эйлера φ от n , и любой из этих генераторов может быть записан как первый узел в цикле (рядом с тождеством e ); или, что более распространено, узлы остаются неотмеченными. Два различных цикла не могут пересекаться в генераторе.
Циклы, содержащие не простое число элементов, имеют циклические подгруппы, которые не показаны на графике. Для группы Dih 4 выше мы могли бы провести линию между a 2 и e , поскольку ( a 2 ) 2 = e , но поскольку a 2 является частью большего цикла, это не ребро графа цикла.
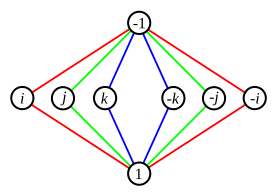
Может возникнуть неоднозначность, когда два цикла разделяют нетождественный элемент. Например, группа кватернионов из 8 элементов имеет график цикла, показанный справа. Каждый из элементов в средней строке при умножении на себя дает −1 (где 1 — тождественный элемент). В этом случае мы можем использовать разные цвета для отслеживания циклов, хотя соображения симметрии также будут работать.
Как отмечалось ранее, два ребра двухэлементного цикла обычно представляются в виде одной линии.
Обратным элементом является узел, симметричный ему в его цикле относительно отражения, фиксирующего тождество.
Граф цикла группы не определен однозначно с точностью до изоморфизма графов ; он также не определяет однозначно группу с точностью до изоморфизма групп . То есть полученный граф зависит от выбранного набора генераторов, и две разные группы (с выбранными наборами генераторов) могут генерировать один и тот же граф цикла. [2]
Для некоторых групп выбор различных элементов для генерации различных примитивных циклов этой группы может привести к различным графам циклов. Примером этого является абелева группа , имеющая порядок 20. [2] Мы обозначаем элемент этой группы как тройку чисел , где и каждое из и равно либо 0, либо 1. Тройка является единичным элементом. На рисунках ниже показано выше и .
Эта группа имеет три примитивных цикла, каждый из которых имеет порядок 10. В первом графе циклов мы выбираем в качестве генераторов этих трех циклов узлы , и . Во втором графе мы генерируем третий из этих циклов --- синий ---, начиная вместо этого с .
Два полученных графа не изоморфны, поскольку имеют диаметры 5 и 4 соответственно.
Две различные (неизоморфные) группы могут иметь графы циклов, которые являются изоморфными , где последний изоморфизм игнорирует метки на узлах графов. Из этого следует, что структура группы не определяется однозначно ее графом циклов.
Пример этого уже имеется для групп порядка 16, двумя группами являются и . Абелева группа является прямым произведением циклических групп порядков 8 и 2. Неабелева группа является полупрямым произведением и , в котором нетождественный элемент отображается в автоморфизм умножения на 5 группы .
При построении циклических графов этих двух групп мы принимаем, что они генерируются элементами s и t с
где последнее отношение делает абелевым. И мы принимаем, что порождается элементами 𝜎 и 𝜏 с
Вот графики циклов для этих двух групп, где мы решили сгенерировать зеленый цикл слева и сгенерировать этот цикл справа:
На правом графике зеленый цикл после перехода от 1 к перемещается рядом с , поскольку
Графы циклов были исследованы теоретиком чисел Дэниелом Шэнксом в начале 1950-х годов в качестве инструмента для изучения мультипликативных групп классов вычетов . [3] Шэнкс впервые опубликовал эту идею в первом издании своей книги « Решенные и нерешенные проблемы теории чисел» в 1962 году . [4] В этой книге Шэнкс исследует, какие группы имеют изоморфные графы циклов и когда граф циклов является планарным . [5] Во втором издании 1978 года Шэнкс размышляет о своих исследованиях групп классов и развитии метода «маленький шаг — гигантский шаг» : [6]
Графы циклов оказались полезными при работе с конечными абелевыми группами; и я часто использовал их для поиска пути в сложной структуре [77, стр. 852], для получения требуемого мультипликативного отношения [78, стр. 426] или для выделения некоторой требуемой подгруппы [79].
Циклические графики используются в качестве педагогического инструмента во вводном учебнике Натана Картера 2009 года « Визуальная теория групп» . [7]
Некоторые типы групп дают типичные графики:
Циклические группы Z n порядка n представляют собой один цикл, графически представленный как n -сторонний многоугольник с элементами в вершинах:
Когда n — простое число , группы вида (Z n ) m будут иметь ( n m − 1)/( n − 1) n -элементных циклов, имеющих общий единичный элемент:
Диэдральные группы Dih n порядка 2 n состоят из n -элементного цикла и n 2-элементных циклов:
Дициклические группы , Dic n = Q 4 n , порядок 4 n :
Другие прямые продукты :
Симметричные группы – Симметричная группа S n содержит для любой группы порядка n подгруппу, изоморфную этой группе. Таким образом, граф циклов каждой группы порядка n будет найден в графе циклов S n .
Смотрите пример: Подгруппы S4
Полная октаэдрическая группа является прямым произведением симметрической группы S 4 и циклической группы Z 2 .
Ее порядок равен 48, и она имеет подгруппы каждого порядка, делящего 48.
В приведенных ниже примерах узлы, которые связаны друг с другом, расположены рядом друг с другом,
поэтому это не самые простые возможные графики циклов для этих групп (как те, что справа).
Как и все графы, граф цикла может быть представлен различными способами, чтобы подчеркнуть различные свойства. Два представления графа цикла S 4 являются примером этого.
{{cite web}}: CS1 maint: местоположение ( ссылка )