Напряжение сдвига

Составляющая напряжения, копланарная с поперечным сечением материала

Сдвигающая сила приложена к верхней части прямоугольника, в то время как нижняя часть удерживается на месте. Результирующее касательное напряжение τ деформирует прямоугольник в параллелограмм . Задействованная площадь будет верхней частью параллелограмма.

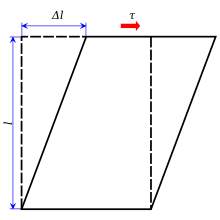
Касательное напряжение (часто обозначается как τ , греч . tau ) — это компонент напряжения , копланарный с поперечным сечением материала . Оно возникает из-за сдвигающей силы , компонента вектора силы, параллельного поперечному сечению материала. Нормальное напряжение , с другой стороны, возникает из-за компонента вектора силы, перпендикулярного поперечному сечению материала, на которое оно действует.

Общее касательное напряжение

Формула для расчета среднего напряжения сдвига τ или силы на единицу площади: ^[1] $${\displaystyle \tau ={F \over A},}$$

где:

• F — приложенная сила;
• А — площадь поперечного сечения.

Рассматриваемая область соответствует поверхности материала , параллельной вектору приложенной силы, т.е. с вектором нормали к поверхности, перпендикулярным силе.

Другие формы

Напряжение сдвига стенки

Касательное напряжение на стенке выражает силу торможения (на единицу площади) от стенки в слоях жидкости, текущей рядом со стенкой. Оно определяется как: где - динамическая вязкость , скорость потока и расстояние от стенки. $${\displaystyle \tau _{w}:=\mu \left.{\frac {\partial u}{\partial y}}\right|_{y=0}}$$ ${\displaystyle \mu }$ ${\displaystyle u}$ ${\displaystyle y}$

Он используется, например, при описании артериального кровотока , и в этом случае есть доказательства того, что он влияет на атерогенный процесс. ^[2]

Чистый

Чистое напряжение сдвига связано с чистой деформацией сдвига , обозначаемой γ , следующим уравнением: ^[3] где G — модуль сдвига изотропного материала, определяемый по формуле Здесь E — модуль Юнга , а ν — коэффициент Пуассона . $${\displaystyle \tau =\gamma G\,}$$ $${\displaystyle G={\frac {E}{2(1+\nu )}}.}$$

Сдвиг балки

Сдвиг балки определяется как внутреннее касательное напряжение балки, вызванное сдвигающей силой, приложенной к балке. $${\displaystyle \tau :={\frac {fQ}{Ib}},}$$

где

• f — общая сила сдвига в рассматриваемом месте;
• Q — статический момент площади ;
• b — толщина (ширина) материала, перпендикулярная сдвигу;
• I — момент инерции всей площади поперечного сечения.

Формула сдвига балки также известна как формула напряжения сдвига Журавского в честь Дмитрия Ивановича Журавского, который вывел ее в 1855 году. ^{[4] [5]}

Полумонококовый сдвиг

Сдвиговые напряжения в полумонококовой конструкции можно рассчитать, идеализировав поперечное сечение конструкции в набор стрингеров (несущих только осевые нагрузки) и стенок (несущих только сдвиговые потоки ). Деление сдвигового потока на толщину заданной части полумонококовой конструкции дает сдвиговое напряжение. Таким образом, максимальное сдвиговое напряжение будет возникать либо в стенке с максимальным сдвиговым потоком, либо с минимальной толщиной.

Конструкции в грунте также могут разрушиться из-за сдвига; например, вес заполненной землей плотины или дамбы может привести к обрушению подпочвы, подобно небольшому оползню .

Ударный сдвиг

Максимальное касательное напряжение, создаваемое в сплошном круглом стержне, подвергающемся удару, определяется по уравнению: ^[6] $${\displaystyle \tau =2{\sqrt {\frac {UG}{V}}},}$$

где

• U — изменение кинетической энергии;
• G , модуль сдвига ;
• V — объем стержня;

и

• U = U _{вращающееся} + U _{приложенное} ;
• U _{вращающийся} = ⁠1/2⁠ Iω ² ;
• U _{приложенное} = Tθ _{смещенное} ;
• I — момент инерции массы;
• ω — угловая скорость.

Напряжение сдвига в жидкостях

Любые реальные жидкости ( включая жидкости и газы ), движущиеся вдоль твердой границы, будут подвергаться сдвиговому напряжению на этой границе. Условие отсутствия скольжения ^[7] диктует, что скорость жидкости на границе (относительно границы) равна нулю; хотя на некоторой высоте от границы скорость потока должна быть равна скорости жидкости. Область между этими двумя точками называется пограничным слоем . Для всех ньютоновских жидкостей в ламинарном потоке сдвиговое напряжение пропорционально скорости деформации в жидкости, где вязкость является константой пропорциональности. Для неньютоновских жидкостей вязкость не является постоянной. Сдвиговое напряжение передается на границу в результате этой потери скорости.

Для ньютоновской жидкости касательное напряжение на элементе поверхности, параллельном плоской пластине в точке y, определяется по формуле: $${\displaystyle \tau (y)=\mu {\frac {\partial u}{\partial y}}}$$

где

• μ — динамическая вязкость потока;
• u — скорость потока вдоль границы;
• y — высота над границей.

В частности, касательное напряжение стенки определяется как: $${\displaystyle \tau _{\mathrm {w} }:=\tau (y=0)=\mu \left.{\frac {\partial u}{\partial y}}\right|_{y=0}~.}$$

Основной закон Ньютона для любой общей геометрии (включая упомянутую выше плоскую пластину) гласит, что тензор сдвига (тензор второго порядка) пропорционален градиенту скорости потока ( скорость является вектором, поэтому ее градиент является тензором второго порядка): $${\displaystyle {\boldsymbol {\tau }}(\mathbf {u} )=\mu {\boldsymbol {\nabla }}\mathbf {u} }$$

и константа пропорциональности называется динамической вязкостью . Для изотропного ньютоновского потока это скаляр, тогда как для анизотропных ньютоновских потоков это может быть и тензор второго порядка. Фундаментальный аспект заключается в том, что для ньютоновской жидкости динамическая вязкость не зависит от скорости потока (т.е. конститутивный закон касательного напряжения линеен ) , тогда как для неньютоновских потоков это неверно, и следует допустить модификацию: $${\displaystyle {\boldsymbol {\tau }}(\mathbf {u} )=\mu (\mathbf {u} ){\boldsymbol {\nabla }}\mathbf {u} }$$

Это уже не закон Ньютона, а общее тензорное тождество: всегда можно найти выражение вязкости как функции скорости потока, если задано любое выражение касательного напряжения как функции скорости потока. С другой стороны, если задано касательное напряжение как функция скорости потока, оно представляет собой ньютоновский поток только в том случае, если его можно выразить как константу для градиента скорости потока. Константа, которую можно найти в этом случае, является динамической вязкостью потока.

Пример

Рассматривая двумерное пространство в декартовых координатах ( x , y ) (компоненты скорости потока соответственно ( u , v )), матрица касательного напряжения, заданная как: представляет собой ньютоновский поток, фактически его можно выразить как: т.е. анизотропный поток с тензором вязкости: который является неоднородным (зависит от пространственных координат) и нестационарным, но, что важно, он не зависит от скорости потока: $${\displaystyle {\begin{pmatrix}\tau _{xx}&\tau _{xy}\\\tau _{yx}&\tau _{yy}\end{pmatrix}}={\begin{pmatrix}x{\frac {\partial u}{\partial x}}&0\\0&-t{\frac {\partial v}{\partial y}}\end{pmatrix}}}$$ $${\displaystyle {\begin{pmatrix}\tau _{xx}&\tau _{xy}\\\tau _{yx}&\tau _{yy}\end{pmatrix}}={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}\cdot {\begin{pmatrix}{\frac {\partial u}{\partial x}}&{\frac {\partial u}{\partial y}}\\{\frac {\partial v}{\partial x}}&{\frac {\partial v}{\partial y}}\end{pmatrix}},}$$ $${\displaystyle {\begin{pmatrix}\mu _{xx}&\mu _{xy}\\\mu _{yx}&\mu _{yy}\end{pmatrix}}={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}}$$ $${\displaystyle {\boldsymbol {\mu }}(x,t)={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}}$$

Этот поток, следовательно, является ньютоновским. С другой стороны, поток, в котором вязкость была: является неньютоновским, поскольку вязкость зависит от скорости потока. Этот неньютоновский поток является изотропным (матрица пропорциональна единичной матрице), поэтому вязкость является просто скаляром: $${\displaystyle {\begin{pmatrix}\mu _{xx}&\mu _{xy}\\\mu _{yx}&\mu _{yy}\end{pmatrix}}={\begin{pmatrix}{\frac {1}{u}}&0\\0&{\frac {1}{u}}\end{pmatrix}}}$$ $${\displaystyle \mu (u)={\frac {1}{u}}}$$

Измерение с помощью датчиков

Датчик напряжения сдвига с расходящимся краем

Это соотношение можно использовать для измерения напряжения сдвига стенки. Если бы датчик мог напрямую измерять градиент профиля скорости на стенке, то умножение на динамическую вязкость дало бы напряжение сдвига. Такой датчик был продемонстрирован А. А. Накви и В. К. Рейнольдсом. ^[8] Интерференционная картина, созданная путем пропускания луча света через две параллельные щели, образует сеть линейно расходящихся полос, которые, по-видимому, исходят из плоскости двух щелей (см. эксперимент с двумя щелями ). Когда частица в жидкости проходит через полосы, приемник обнаруживает отражение картины полос. Сигнал можно обработать, и, зная угол полосы, можно экстраполировать высоту и скорость частицы. Измеренное значение градиента скорости стенки не зависит от свойств жидкости и, как следствие, не требует калибровки. Последние достижения в области технологий микрооптического производства сделали возможным использование интегрированного дифракционного оптического элемента для изготовления датчиков напряжения сдвига с расходящимися полосами, которые можно использовать как в воздухе, так и в жидкости. ^[9]

Датчик напряжения сдвига с микростолбом

Еще один метод измерения — это тонкие настенные микростолбы из гибкого полимера PDMS, которые изгибаются в ответ на приложенные силы сопротивления вблизи стенки. Датчик, таким образом, относится к принципам косвенного измерения, основанным на соотношении между градиентами скорости вблизи стенки и локальным напряжением сдвига стенки. ^{[10] [11]}

Электродиффузионный метод

Электродиффузионный метод измеряет скорость сдвига стенки в жидкой фазе от микроэлектрода в условиях предельного диффузионного тока. Разность потенциалов между анодом с широкой поверхностью (обычно расположенным вдали от измерительной области) и небольшим рабочим электродом, действующим как катод, приводит к быстрой окислительно-восстановительной реакции. Исчезновение ионов происходит только на активной поверхности микрозонда, вызывая развитие диффузионного пограничного слоя, в котором скорость быстрой электродиффузионной реакции контролируется только диффузией. Разрешение конвективно-диффузионного уравнения в пристеночной области микроэлектрода приводит к аналитическим решениям, полагающимся на характерную длину микрозондов, диффузионные свойства электрохимического раствора и скорость сдвига стенки. ^[12]

Смотрите также

• Критическое разрешенное напряжение сдвига
• Прямой тест на сдвиг
• Трение
• Диаграммы сдвига и момента
• Скорость сдвига
• Деформация сдвига
• Прочность на сдвиг
• Растягивающее напряжение
• Испытание на трехосный сдвиг

Ссылки

1. Хиббелер, RC (2004). Механика материалов . Нью-Джерси, США: Pearson Education. стр. 32. ISBN 0-13-191345-X.
2. Katritsis, Demosthenes (2007). «Напряжение сдвига стенки: теоретические соображения и методы измерения». Прогресс в сердечно-сосудистых заболеваниях . 49 (5): 307–329. doi :10.1016/j.pcad.2006.11.001. PMID  17329179.
3. "Сопротивление материалов". Eformulae.com . Получено 24 декабря 2011 г. .
4. Лекция Формула Журавского [Формула Журавского]. Сопромат Лекции (на русском языке) . Проверено 26 февраля 2014 г.
5. "Изгиб балок" (PDF) . Лекции по машиностроению . Университет Макмастера .^{[ постоянная мертвая ссылка ]}
6. LLC., Engineers Edge. "Уравнения напряжения сдвига и их применение". engineersedge.com . Получено 29.08.2024 .
7. Дэй, Майкл А. (2004), «Условие отсутствия проскальзывания в динамике жидкости», Erkenntnis , 33 (3), Springer Netherlands: 285–296, doi : 10.1007/BF00717588, ISSN  0165-0106, S2CID  55186899.
8. Накви, АА; Рейнольдс, ВК (январь 1987 г.), «Двойной цилиндрический волновой лазерно-доплеровский метод измерения трения кожи в потоке жидкости», Технический отчет NASA STI/Recon N , 87
9. {Датчик напряжения сдвига microS, MSE}
10. Гроссе, С.; Шредер, В. (2009), «Двумерная визуализация турбулентного напряжения сдвига стенки с использованием микростолбиков», Журнал AIAA , 47 (2): 314–321, Bibcode : 2009AIAAJ..47..314G, doi : 10.2514/1.36892
11. Große, S.; Schröder, W. (2008), "Динамические измерения напряжения сдвига стенки в турбулентном потоке в трубе с использованием микростолбчатого датчика MPS ³ ", Международный журнал по теплу и потокам жидкости , 29 (3): 830–840, Bibcode : 2008IJHFF..29..830G, doi : 10.1016/j.ijheatfluidflow.2008.01.008
12. Havlica, J.; Kramolis, D.; Huchet, F. (2021), «Пересмотр электродиффузионной теории для измерения напряжения сдвига стенки» (PDF) , Международный журнал по тепло- и массообмену , 165 : 120610, Bibcode : 2021IJHMT.16520610H, doi : 10.1016/j.ijheatmasstransfer.2020.120610, S2CID  228876357