Закон квадрата-куба

Соотношение между площадью поверхности и объемом по мере увеличения размера

Закон квадрата-куба впервые был упомянут в «Двух новых науках» (1638).

Закон квадрата-куба (или закон куба-квадрата ) — это математический принцип, применяемый в различных научных областях, который описывает соотношение между объемом и площадью поверхности по мере увеличения или уменьшения размера фигуры. Впервые он был ^{[ сомнительный – обсудить ]} описан в 1638 году Галилео Галилеем в его «Двух новых науках» как «... отношение двух объемов больше отношения их поверхностей». ^[1]

Этот принцип гласит, что по мере увеличения размера формы ее объем растет быстрее, чем площадь ее поверхности. Применительно к реальному миру этот принцип имеет множество следствий, которые важны в различных областях, от машиностроения до биомеханики . Он помогает объяснить такие явления, как, например, почему крупным млекопитающим, таким как слоны, сложнее охлаждаться, чем мелким, таким как мыши, и почему строительство все более высоких небоскребов становится все сложнее.

Описание

Графики площади поверхности, A против объема, V Платоновых тел и сферы, показывающие, что отношение площади поверхности к объему уменьшается с увеличением объема.

Пунктирные стрелки показывают, что при увеличении объема в 8 (2³) раз площадь поверхности увеличивается в 4 (2²) раза.

Эта картинка поясняет связь между длиной стороны многогранника, площадью его поверхности и его объемом.

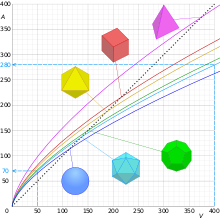
Закон квадрата-куба можно сформулировать следующим образом:

Когда объект пропорционально увеличивается в размерах, его новая площадь поверхности пропорциональна квадрату множителя, а его новый объем пропорционален кубу множителя.

Математически это выглядит так: ^[2] где — исходная площадь поверхности, — новая площадь поверхности. где — исходный объем, — новый объем, — исходная длина, — новая длина. $${\displaystyle A_{2}=A_{1}\left({\frac {\ell _{2}}{\ell _{1}}}\right)^{2}}$$ ${\displaystyle A_{1}}$ ${\displaystyle A_{2}}$ $${\displaystyle V_{2}=V_{1}\left({\frac {\ell _{2}}{\ell _{1}}}\right)^{3}}$$ ${\displaystyle V_{1}}$ ${\displaystyle V_{2}}$ ${\displaystyle \ell _{1}}$ ${\displaystyle \ell _{2}}$

Например, куб с длиной стороны 1 метр имеет площадь поверхности 6 м ² и объем 1 м ³ . Если стороны куба умножить на 2, его площадь поверхности умножится на квадрат 2 и станет 24 м ² . Его объем умножится на куб 2 и станет 8 м ³ .

Исходный куб (сторона 1 м) имеет отношение площади поверхности к объему 6:1. Более крупный куб (сторона 2 м) имеет отношение площади поверхности к объему (24/8) 3:1. По мере увеличения размеров объем будет продолжать расти быстрее, чем площадь поверхности. Таким образом, закон квадрата-куба. Этот принцип применим ко всем твердым телам. ^[3]

Приложения

Инженерное дело

Когда физический объект сохраняет ту же плотность и масштабируется, его объем и масса увеличиваются на куб множителя, тогда как его площадь поверхности увеличивается только на квадрат того же множителя. Это означало бы, что когда большая версия объекта ускоряется с той же скоростью, что и оригинал, большее давление будет оказываться на поверхность большего объекта.

Рассмотрим простой пример тела массой , подвергающегося ускорению , с площадью поверхности , на которую действует ускоряющая сила . Сила, вызванная ускорением, равна , а давление равно . ${\displaystyle m}$ ${\displaystyle a}$ ${\displaystyle A}$ ${\displaystyle F=ma}$ ${\displaystyle P={\frac {F}{A}}={\frac {ma}{A}}}$

Теперь представьте, что объект увеличен на множитель, так что он имеет новую массу и новую площадь поверхности . ${\displaystyle x}$ ${\displaystyle m'=x^{3}m}$ ${\displaystyle A'=x^{2}A}$

Новая сила, вызванная ускорением, равна , а результирующее давление равно: ${\displaystyle F'=x^{3}ma}$ $${\displaystyle {\begin{aligned}P'&={\frac {F'}{A'}}\\&={\frac {x^{3}ma}{x^{2}A}}\\&=x\ {\frac {ma}{A}}\\&=x\ P\\\end{aligned}}}$$

Таким образом, простое увеличение размера объекта, сохранение того же материала конструкции (плотности) и того же ускорения увеличит давление на тот же коэффициент масштабирования. Это будет означать, что объект будет иметь меньшую способность противостоять напряжению и будет более склонен к разрушению при ускорении.

Вот почему большие транспортные средства плохо показывают себя в краш-тестах и ​​почему существуют теоретические ограничения относительно того, насколько высокими могут быть построены здания. Аналогично, чем больше объект, тем меньше другие объекты будут сопротивляться его движению, вызывая его замедление.

Примеры инженерных разработок

• Паровой двигатель : Джеймсу Уатту , работавшему инструментальным мастером в Университете Глазго , дали масштабную модель парового двигателя Ньюкомена для приведения его в рабочее состояние. Уатт понял, что проблема связана с законом квадрата-куба, поскольку отношение поверхности к объему цилиндра модели было больше, чем у гораздо более крупных коммерческих двигателей, что приводило к чрезмерной потере тепла. ^[4] Эксперименты с этой моделью привели к знаменитым усовершенствованиям Уатта в паровом двигателе.

Boeing 737-500 перед Airbus A380

• Airbus A380 : подъемные и управляющие поверхности (крылья, рули направления и высоты) относительно велики по сравнению с фюзеляжем самолета. Например, если взять Boeing 737 и просто увеличить его размеры до размеров A380, то крылья будут слишком малы для веса самолета из-за правила квадрата-куба.
• Ракетные двигатели с детандерным циклом страдают от закона квадрата-куба. Их размер, а следовательно, и тяга, ограничены эффективностью теплопередачи из-за того, что площадь поверхности сопла увеличивается медленнее, чем объем топлива, протекающего через сопло.
• Клиперу требуется относительно больше парусной поверхности, чем шлюпу , чтобы достичь той же скорости, то есть отношение площади парусности к площади парусности у этих судов выше, чем отношение веса к весу .
• Аэростаты обычно выигрывают от закона квадрата-куба. По мере увеличения радиуса ( ) ${\displaystyle r^{1}}$ воздушного шара стоимость площади поверхности увеличивается квадратично ( ) ${\displaystyle r^{2}}$ , но подъемная сила, создаваемая объемом, увеличивается кубически ( ) ${\displaystyle r^{3}}$ .
• Структурная инженерия : Материалы, которые работают в малых масштабах, могут не работать в больших масштабах. Например, сжимающее напряжение в нижней части небольшой отдельно стоящей колонны масштабируется с той же скоростью, что и размер колонны. Следовательно, существует размер для данного материала и плотности, при котором колонна разрушится сама по себе.

Биомеханика

Если бы животное было изометрически увеличено на значительную величину, его относительная мышечная сила была бы сильно уменьшена, поскольку поперечное сечение его мышц увеличилось бы на квадрат масштабного фактора, а его масса увеличилась бы на куб масштабного фактора. В результате этого сердечно-сосудистые и дыхательные функции были бы сильно нагружены.

В случае летающих животных нагрузка на крыло увеличилась бы, если бы они были изометрически увеличены, и поэтому им пришлось бы лететь быстрее, чтобы получить ту же величину подъемной силы . Сопротивление воздуха на единицу массы также выше для более мелких животных (снижая конечную скорость ), поэтому небольшое животное, такое как муравей, не может получить серьезную травму от удара о землю после падения с любой высоты.

Как утверждает Дж. Б. С. Холдейн , крупные животные не выглядят как мелкие: слона нельзя спутать с мышью, увеличенной в размерах. Это происходит из-за аллометрического масштабирования : кости слона обязательно пропорционально намного больше костей мыши, поскольку они должны нести пропорционально больший вес. Холдейн иллюстрирует это в своем основополагающем эссе 1928 года « О правильном размере» , ссылаясь на аллегорических гигантов: «... представьте себе человека ростом 60 футов... Гигантский Папа и Гигантский Язычник в иллюстрированном « Путешествии паломника»: ... Эти монстры... весили в 1000 раз больше [обычного человека]. Каждый квадратный дюйм гигантской кости должен был выдерживать вес, в 10 раз превышающий вес квадратного дюйма человеческой кости. Поскольку средняя бедренная кость человека ломается под действием веса, примерно в 10 раз превышающего человеческий, Поуп и Язычник ломали бы бедра каждый раз, когда делали шаг». ^[5] Следовательно, большинство животных демонстрируют аллометрическое масштабирование с увеличением размера, как среди видов, так и внутри вида. Гигантские существа, которые можно увидеть в фильмах о монстрах (например, Годзилла , Кинг-Конг и они! и другие кайдзю ), также нереалистичны, учитывая, что их огромные размеры заставили бы их рухнуть.

Однако плавучесть воды в некоторой степени сводит на нет действие гравитации. Поэтому водные животные могут достигать очень больших размеров без тех же скелетно-мышечных структур, которые требуются для наземных животных аналогичного размера, и это главная причина того, что самые большие животные, когда-либо существовавшие на Земле, являются водными животными .

Скорость метаболизма животных масштабируется с помощью математического принципа, называемого четвертной степенью масштабирования ^[6] в соответствии с метаболической теорией экологии .

Массо- и теплопередача

Массоперенос, такой как диффузия к более мелким объектам, таким как живые клетки, происходит быстрее, чем диффузия к более крупным объектам, таким как целые животные. Таким образом, в химических процессах, которые происходят на поверхности, а не в объеме, более мелкодисперсный материал более активен. Например, активность гетерогенного катализатора выше , когда он разделен на более мелкие частицы. Такие катализаторы обычно возникают в более теплых условиях.

Выработка тепла в результате химического процесса масштабируется пропорционально кубу линейного размера (высота, ширина) сосуда, но площадь поверхности сосуда масштабируется только квадратом линейного размера. Следовательно, более крупные сосуды гораздо сложнее охлаждать. Кроме того, крупномасштабные трубопроводы для передачи горячих жидкостей трудно моделировать в малых масштабах, поскольку тепло быстрее передается из более мелких труб. Непринятие этого во внимание при проектировании процесса может привести к катастрофическому тепловому разгону .

Смотрите также

• Биомеханика
• Аллометрический закон
• On Being the Right Size , эссе Дж. Б. С. Холдейна , в котором рассматриваются изменения в форме животных, которые потребуются при большом изменении размера. Также см. выше пример аллегорических гигантов при масштабировании размера.
• Отношение площади поверхности к объему
• Закон Клейбера
• Правило Бергмана

Ссылки

1. Дэвид Х. Аллен (24 сентября 2013 г.). Как механика сформировала современный мир. Springer. ISBN 9783319017013.
2. "World Builders: The Sizes of Living Things". world-builders.org . Архивировано из оригинала 2016-10-23 . Получено 2012-04-21 .
3. Майкл С. ЛаБарбера. «Биология монстров из фильмов категории B».
4. Розен, Уильям (2012). Самая мощная идея в мире: история пара, промышленности и изобретения . Издательство Чикагского университета. стр. 98. ISBN 978-0226726342.
5. Холдейн, Дж. Б. С. «О правильном размере». Лаборатория интернет-исследований. Калифорнийский университет в Лос-Анджелесе. Архивировано из оригинала 22 августа 2011 г. Получено 1 апреля 2017 г.
6. Джордж Джонсон (12 января 1999 г.). «О мышах и слонах: вопрос масштаба». The New York Times . Получено 11 июня 2015 г.

Внешние ссылки

• Учебные материалы по теме «Пропорции» в Викиверситете