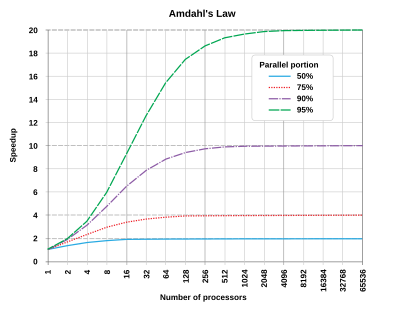
В компьютерной архитектуре закон Амдаля (или аргумент Амдаля [1] ) представляет собой формулу, которая дает теоретическое ускорение задержки выполнения задачи при фиксированной рабочей нагрузке , которое можно ожидать от системы, ресурсы которой улучшены .
Закон можно сформулировать следующим образом:
«Общее улучшение производительности, достигаемое за счет оптимизации одной части системы, ограничивается долей времени, в течение которого улучшенная часть фактически используется». [2]
Он назван в честь ученого-компьютерщика Джина Амдаля и был представлен на Весенней совместной компьютерной конференции Американской федерации обществ обработки информации (AFIPS) в 1967 году.
Закон Амдаля часто используется в параллельных вычислениях для прогнозирования теоретического ускорения при использовании нескольких процессоров. Например, если программе требуется 20 часов для завершения с использованием одного потока, и часть программы продолжительностью один час не может быть распараллелена, то только оставшиеся 19 часов ( p = 0,95 ) времени выполнения могут быть распараллелены. Поэтому, независимо от того, сколько потоков выделено на параллельное выполнение этой программы, минимальное время выполнения всегда больше 1 часа. Следовательно, теоретическое ускорение составляет максимум 20-кратную производительность одного потока, .
Универсальный закон масштабируемости (USL), разработанный Нилом Дж. Гюнтером , расширяет закон Амдаля и учитывает дополнительные накладные расходы из-за межпроцессного взаимодействия. USL количественно определяет масштабируемость на основе таких параметров, как конкуренция и согласованность. [3]
Закон Амдаля можно сформулировать следующим образом: [4]
где
Более того,
показывает, что теоретическое ускорение выполнения всей задачи увеличивается с улучшением ресурсов системы и что независимо от величины улучшения теоретическое ускорение всегда ограничено той частью задачи, которая не может получить выгоду от улучшения.
Закон Амдаля применим только к случаям, когда размер проблемы фиксирован. На практике, по мере того, как становится доступно больше вычислительных ресурсов, они, как правило, используются для более крупных задач (больших наборов данных), и время, затрачиваемое на параллелизуемую часть, часто растет гораздо быстрее, чем на изначально последовательную работу. В этом случае закон Густафсона дает менее пессимистичную и более реалистичную оценку параллельной производительности. [5]
Задачу, выполняемую системой, ресурсы которой улучшены по сравнению с исходной аналогичной системой, можно разделить на две части:
Примером может служить компьютерная программа, обрабатывающая файлы. Часть этой программы может сканировать каталог диска и создавать список файлов внутри памяти. После этого другая часть программы передает каждый файл в отдельный поток для обработки. Часть, которая сканирует каталог и создает список файлов, не может быть ускорена на параллельном компьютере, но часть, которая обрабатывает файлы, может.
Время выполнения всей задачи до улучшения ресурсов системы обозначается как . Оно включает время выполнения той части, которая не получит выгоду от улучшения ресурсов, и время выполнения той, которая получит выгоду от этого. Доля времени выполнения задачи, которая получит выгоду от улучшения ресурсов, обозначается как . Та, которая касается части, которая не получит выгоду от этого, поэтому равна . Тогда:
Именно выполнение той части, которая выигрывает от улучшения ресурсов, ускоряется фактором после улучшения ресурсов. Следовательно, время выполнения той части, которая не выигрывает от этого, остается прежним, в то время как часть, которая выигрывает от этого, становится:
Теоретическое время выполнения всей задачи после улучшения ресурсов составит:
Закон Амдаля дает теоретическое ускорение задержки выполнения всей задачи при фиксированной рабочей нагрузке , что дает
Если 30% времени выполнения может быть предметом ускорения, p будет равно 0,3; если улучшение делает затронутую часть в два раза быстрее, s будет равно 2. Закон Амдаля гласит, что общее ускорение от применения улучшения составит:
Например, предположим, что нам дана последовательная задача, которая разделена на четыре последовательные части, проценты времени выполнения которых составляют p 1 = 0,11 , p 2 = 0,18 , p 3 = 0,23 и p 4 = 0,48 соответственно. Затем нам говорят, что 1-я часть не ускорена, поэтому s 1 = 1 , в то время как 2-я часть ускорена в 5 раз, поэтому s 2 = 5 , 3-я часть ускорена в 20 раз, поэтому s 3 = 20 , а 4-я часть ускорена в 1,6 раза, поэтому s 4 = 1,6 . Используя закон Амдаля, общее ускорение равно
Обратите внимание, что ускорение 2-й и 3-й частей в 5 и 20 раз соответственно не оказывает большого влияния на общее ускорение, тогда как 4-я часть (48% времени выполнения) ускоряется всего в 1,6 раза.
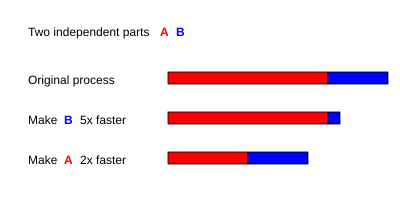
Например, с последовательной программой из двух частей A и B, для которой T A = 3 с и T B = 1 с ,
Поэтому, заставить часть A работать в 2 раза быстрее лучше, чем заставить часть B работать в 5 раз быстрее. Процентное улучшение скорости можно рассчитать как
Если непараллелизуемая часть оптимизирована в множитель , то
Из закона Амдаля следует, что ускорение за счет параллелизма определяется выражением
Когда , то имеем , что означает, что ускорение измеряется относительно времени выполнения после оптимизации непараллелизуемой части.
Когда ,
Если , и , то:
Далее рассмотрим случай, когда непараллелизуемая часть уменьшается в раз , а параллелизуемая часть соответственно увеличивается. Тогда
Из закона Амдаля следует, что ускорение за счет параллелизма определяется выражением
Закон Амдаля часто путают с законом убывающей отдачи , тогда как только частный случай применения закона Амдаля демонстрирует закон убывающей отдачи. Если оптимально (с точки зрения достигнутого ускорения) выбрать то, что должно быть улучшено, то можно будет увидеть монотонно уменьшающиеся улучшения по мере улучшения. Если же выбрать неоптимально, то после улучшения неоптимального компонента и перехода к улучшению более оптимального компонента можно увидеть увеличение отдачи. Обратите внимание, что часто рационально улучшать систему в порядке, который является «неоптимальным» в этом смысле, учитывая, что некоторые улучшения сложнее или требуют большего времени разработки, чем другие.
Закон Амдаля представляет собой закон убывающей доходности, если мы рассматриваем, какой доход мы получаем, добавляя больше процессоров к машине, если мы запускаем вычисление фиксированного размера, которое будет использовать все доступные процессоры по их мощности. Каждый новый процессор, добавленный в систему, будет добавлять меньше полезной мощности, чем предыдущий. Каждый раз, когда мы удваиваем количество процессоров, коэффициент ускорения будет уменьшаться, поскольку общая пропускная способность приближается к пределу 1/(1 − p ).
Этот анализ не учитывает другие потенциальные узкие места, такие как пропускная способность памяти и пропускная способность ввода-вывода. Если эти ресурсы не масштабируются с числом процессоров, то простое добавление процессоров обеспечивает еще меньшую отдачу.
Следствием закона Амдаля является то, что для ускорения реальных приложений, которые имеют как последовательные, так и параллельные части, требуются гетерогенные вычислительные методы. [6] Существуют новые модели ускорения и потребления энергии, основанные на более общем представлении гетерогенности, называемом гетерогенностью нормальной формы, которые поддерживают широкий спектр гетерогенных многоядерных архитектур. Эти методы моделирования направлены на прогнозирование энергоэффективности системы и диапазонов производительности, а также облегчают исследования и разработки на уровне аппаратного и системного программного обеспечения. [7] [8]