Интервальное дерево

Древовидная структура данных для хранения интервалов

В информатике интервальное дерево — это древовидная структура данных для хранения интервалов . В частности, оно позволяет эффективно находить все интервалы, которые перекрываются с любым заданным интервалом или точкой. Оно часто используется для оконных запросов, ^[1] например, для поиска всех дорог на компьютерной карте внутри прямоугольного окна просмотра или для поиска всех видимых элементов внутри трехмерной сцены. Похожая структура данных — сегментное дерево .

Тривиальное решение — посетить каждый интервал и проверить, пересекает ли он заданную точку или интервал, что требует времени, где — количество интервалов в коллекции. Поскольку запрос может возвращать все интервалы, например, если запрос представляет собой большой интервал, пересекающий все интервалы в коллекции, это асимптотически оптимально ; однако мы можем добиться большего, рассмотрев алгоритмы, чувствительные к выходным данным , где время выполнения выражается через , количество интервалов, созданных запросом. Деревья интервалов имеют время запроса и начальное время создания , при этом ограничивая потребление памяти до . После создания деревья интервалов могут быть динамическими, что позволяет эффективно вставлять и удалять интервал во времени. Если конечные точки интервалов находятся в пределах небольшого целочисленного диапазона ( например , в диапазоне ), существуют более быстрые и фактически оптимальные структуры данных ^{[2] [3]} с временем предварительной обработки и временем запроса для представления интервалов, содержащих заданную точку запроса (см. ^[2] для очень простого примера). ${\displaystyle O(n)}$ ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle O(\log n+m)}$ ${\displaystyle O(n\log n)}$ ${\displaystyle O(n)}$ ${\displaystyle O(\log n)}$ ${\displaystyle [1,\ldots ,O(n)]}$ ${\displaystyle O(n)}$ ${\displaystyle O(1+m)}$ ${\displaystyle m}$

Наивный подход

В простом случае интервалы не перекрываются, и их можно вставить в простое двоичное дерево поиска и запросить по времени. Однако при произвольном перекрытии интервалов нет возможности сравнить два интервала для вставки в дерево, поскольку упорядочения, отсортированные по начальным или конечным точкам, могут быть разными. Наивный подход может заключаться в построении двух параллельных деревьев, одно из которых упорядочено по начальной точке, а другое — по конечной точке каждого интервала. Это позволяет со временем отбросить половину каждого дерева , но результаты должны быть объединены, что требует времени. Это дает нам запросы в , что не лучше, чем перебор. ${\displaystyle O(\log n)}$ ${\displaystyle O(\log n)}$ ${\displaystyle O(n)}$ ${\displaystyle O(n+\log n)=O(n)}$

Интервальные деревья решают эту проблему. В этой статье описываются два альтернативных проекта интервального дерева, названные центрированным интервальным деревом и дополненным деревом .

Центрированное интервальное дерево

Запросы требуют времени, причем общее число интервалов равно числу представленных результатов. Построение требует времени, а хранение требует места. ${\displaystyle O(\log n+m)}$ ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle O(n\log n)}$ ${\displaystyle O(n)}$

Строительство

Имея набор интервалов на числовой прямой, мы хотим построить структуру данных, чтобы можно было эффективно извлекать все интервалы, перекрывающие другой интервал или точку. ${\displaystyle n}$

Начнем с того, что возьмем весь диапазон всех интервалов и разделим его пополам в точке (на практике следует выбирать, чтобы дерево оставалось относительно сбалансированным). Это даст три набора интервалов: те, что полностью слева, которые мы назовем , те, что полностью справа, которые мы назовем , и те, что перекрываются, которые мы назовем . ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle S_{\textrm {left}}}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle S_{\textrm {right}}}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle S_{\textrm {center}}}$

Интервалы в и рекурсивно делятся таким же образом до тех пор, пока не останется ни одного интервала. ${\displaystyle S_{\textrm {left}}}$ ${\displaystyle S_{\textrm {right}}}$

Интервалы, которые перекрывают центральную точку, хранятся в отдельной структуре данных, связанной с узлом в дереве интервалов. Эта структура данных состоит из двух списков, один из которых содержит все интервалы, отсортированные по начальным точкам, а другой — все интервалы, отсортированные по конечным точкам. ${\displaystyle S_{\textrm {center}}}$

Результатом является двоичное дерево , в каждом узле которого хранится:

• Центральная точка
• Указатель на другой узел, содержащий все интервалы полностью слева от центральной точки
• Указатель на другой узел, содержащий все интервалы полностью справа от центральной точки
• Все интервалы, перекрывающие центральную точку, отсортированы по начальной точке
• Все интервалы, перекрывающие центральную точку, отсортированные по их конечной точке

Пересекающиеся

Учитывая построенную выше структуру данных, мы получаем запросы, состоящие из диапазонов или точек, и возвращаем все диапазоны в исходном наборе, перекрывающие эти входные данные.

С точкой

Задача состоит в том, чтобы найти все интервалы в дереве, которые перекрывают заданную точку . Дерево обходит с помощью аналогичного рекурсивного алгоритма, который использовался бы для обхода традиционного бинарного дерева, но с дополнительной логикой для поддержки поиска интервалов, перекрывающих «центральную» точку в каждом узле. ${\displaystyle x}$

Для каждого узла дерева сравнивается с , средней точкой, используемой при построении узла выше. Если меньше , рассматривается самый левый набор интервалов, ,. Если больше , рассматривается самый правый набор интервалов, ,. ${\displaystyle x}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle x}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle S_{\textrm {left}}}$ ${\displaystyle x}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle S_{\textrm {right}}}$

Все интервалы в , которые начинаются до , должны перекрываться, если меньше . Аналогично, тот же метод применяется и при проверке заданного интервала. Если заданный интервал заканчивается в y и y меньше , все интервалы в , которые начинаются до y, также должны перекрывать заданный интервал. ${\displaystyle S_{\textrm {center}}}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x_{\textrm {center}}}$
${\displaystyle x_{\textrm {center}}}$ ${\displaystyle S_{\textrm {center}}}$

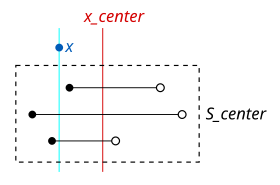
Поскольку каждый узел обрабатывается при прохождении дерева от корня до листа, диапазоны в нем обрабатываются. Если меньше , мы знаем, что все интервалы в заканчиваются после , или они не могут также перекрываться . Поэтому нам нужно найти только те интервалы в , которые начинаются до . Мы можем обратиться к спискам , которые уже были построены. Поскольку в этом сценарии нас интересуют только начала интервалов, мы можем обратиться к списку, отсортированному по началам. Предположим, мы находим ближайшее число, не большее, чем в этом списке. Все диапазоны от начала списка до этой найденной точки перекрываются, потому что они начинаются до и заканчиваются после (как мы знаем, потому что они перекрываются, что больше, чем ). Таким образом, мы можем просто начать перечислять интервалы в списке, пока начальное значение не превысит . ${\displaystyle S_{\textrm {center}}}$ ${\displaystyle x}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle S_{\textrm {center}}}$ ${\displaystyle x}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle S_{\textrm {center}}}$ ${\displaystyle x}$ ${\displaystyle S_{\textrm {center}}}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle x}$ ${\displaystyle x}$

Аналогично, если больше , мы знаем, что все интервалы в должны начинаться до , поэтому мы находим те интервалы, которые заканчиваются после , используя список, отсортированный по окончаниям интервалов. ${\displaystyle x}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle S_{\textrm {center}}}$ ${\displaystyle x}$ ${\displaystyle x}$

Если точно совпадает , все интервалы можно добавить к результатам без дальнейшей обработки, а обход дерева можно остановить. ${\displaystyle x}$ ${\displaystyle x_{\textrm {center}}}$ ${\displaystyle S_{\textrm {center}}}$

С интервалом

Чтобы интервал результата пересекал интервал нашего запроса, должно выполняться одно из следующих условий: ${\displaystyle r}$ ${\displaystyle q}$

• либо начальная, либо конечная точка находится в ; или ${\displaystyle r}$ ${\displaystyle q}$
• ${\displaystyle r}$полностью закрывает . ${\displaystyle q}$

Сначала мы находим все интервалы с начальными и/или конечными точками внутри , используя отдельно построенное дерево. В одномерном случае мы можем использовать дерево поиска, содержащее все начальные и конечные точки в наборе интервалов, каждая из которых имеет указатель на свой соответствующий интервал. Двоичный поиск по времени для начала и конца выявляет минимальные и максимальные точки для рассмотрения. Каждая точка в этом диапазоне ссылается на интервал, который перекрывается и добавляется в список результатов. Необходимо соблюдать осторожность, чтобы избежать дубликатов, поскольку интервал может как начинаться, так и заканчиваться в пределах . Это можно сделать с помощью бинарного флага на каждом интервале, чтобы отметить, был ли он добавлен в набор результатов. ${\displaystyle q}$ ${\displaystyle O(\log n)}$ ${\displaystyle q}$ ${\displaystyle q}$ ${\displaystyle q}$

Наконец, мы должны найти интервалы, которые охватывают . Чтобы найти их, мы выбираем любую точку внутри и используем алгоритм выше, чтобы найти все интервалы, пересекающие эту точку (опять же, внимательно удаляя дубликаты). ${\displaystyle q}$ ${\displaystyle q}$

Более высокие измерения

Структуру данных интервального дерева можно обобщить до более высокого измерения с идентичным временем и пространством запроса и построения. ${\displaystyle N}$ ${\displaystyle O(n\log n)}$

Сначала строится дерево диапазонов в измерениях, которое позволяет эффективно извлекать все интервалы с начальными и конечными точками внутри области запроса . После того, как соответствующие диапазоны найдены, единственное, что остается, это те диапазоны, которые охватывают область в некотором измерении. Чтобы найти эти перекрытия, создаются деревья интервалов, и для каждого запрашивается одно пересечение осей. Например, в двух измерениях нижняя часть квадрата (или любая другая горизонтальная линия, пересекающая ) будет запрошена по дереву интервалов, построенному для горизонтальной оси. Аналогично, левая часть (или любая другая вертикальная линия, пересекающая ) будет запрошена по дереву интервалов, построенному на вертикальной оси. ${\displaystyle N}$ ${\displaystyle R}$ ${\displaystyle N}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle R}$ ${\displaystyle R}$

Каждое интервальное дерево также нуждается в дополнении для более высоких измерений. В каждом узле, который мы проходим по дереву, сравнивается с для поиска перекрытий. Вместо двух отсортированных списков точек, которые использовались в одномерном случае, строится дерево диапазонов. Это позволяет эффективно извлекать все точки в этой области перекрытия . ${\displaystyle x}$ ${\displaystyle S_{\textrm {center}}}$ ${\displaystyle S_{\textrm {center}}}$ ${\displaystyle R}$

Удаление

Если после удаления интервала из дерева, узел, содержащий этот интервал, не содержит больше интервалов, этот узел может быть удален из дерева. Это сложнее, чем обычная операция удаления бинарного дерева.

Интервал может перекрывать центральную точку нескольких узлов в дереве. Поскольку каждый узел хранит интервалы, которые его перекрывают, причем все интервалы полностью слева от его центральной точки в левом поддереве, аналогично для правого поддерева, следует, что каждый интервал хранится в узле, ближайшем к корню из набора узлов, центральную точку которых он перекрывает.

Обычные операции удаления в двоичном дереве (в случае, когда удаляемый узел имеет двух дочерних элементов) включают в себя перемещение узла дальше от листа к позиции удаляемого узла (обычно это самый левый дочерний элемент правого поддерева или самый правый дочерний элемент левого поддерева).

Удаление узла с двумя дочерними узлами из двоичного дерева поиска с использованием предшественника в прямом порядке (самый правый узел в левом поддереве, обозначенный 6 ).

В результате этого продвижения некоторые узлы, которые были выше продвигаемого узла, станут его потомками; необходимо выполнить поиск этих узлов на предмет интервалов, которые также перекрывают продвигаемый узел, и переместить эти интервалы в продвигаемый узел. Как следствие, это может привести к появлению новых пустых узлов, которые необходимо удалить, следуя тому же алгоритму снова.

Балансировка

Те же проблемы, которые влияют на удаление, влияют и на операции вращения; вращение должно сохранять инвариант, что узлы хранятся как можно ближе к корню.

Дополненное дерево

Расширенное дерево с низким значением в качестве ключа и максимально высоким значением в качестве дополнительной аннотации.

Например, при проверке, перекрывает ли заданный интервал [40 ,60) интервалы в дереве, показанном выше, мы видим, что он не перекрывает интервал [20, 36) в корне, но поскольку нижнее значение корня (20) меньше искомого верхнего значения (60), мы должны выполнить поиск в правом поддереве. Максимальное верхнее значение левого поддерева 41 превышает искомое нижнее значение (40), поэтому мы должны выполнить поиск и в левом поддереве. Однако оба потомка узла [3, 41) имеют максимальные верхние значения меньше 40, поэтому поиск в левом поддереве на этом заканчивается, и нет необходимости выполнять их поиск.

Другой способ представления интервалов описан в работе Кормена и др. (2009, раздел 14.3: Деревья интервалов, стр. 348–354).

Как вставка, так и удаление требуют времени, представляющего собой общее количество интервалов в дереве до операции вставки или удаления. ${\displaystyle O(\log n)}$ ${\displaystyle n}$

Дополненное дерево может быть построено из простого упорядоченного дерева, например, двоичного дерева поиска или самобалансирующегося двоичного дерева поиска , упорядоченного по «низким» значениям интервалов. Затем к каждому узлу добавляется дополнительная аннотация, записывающая максимальное верхнее значение среди всех интервалов от этого узла вниз. Поддержание этого атрибута включает обновление всех предков узла снизу вверх всякий раз, когда узел добавляется или удаляется. Это занимает всего O( h ) шагов на добавление или удаление узла, где h — высота узла, добавленного или удаленного в дереве. Если во время вставки и удаления происходят какие-либо повороты дерева , затронутые узлы также могут нуждаться в обновлении.

Теперь известно, что два интервала и пересекаются только тогда, когда оба и . При поиске в деревьях узлов, пересекающихся с заданным интервалом, можно сразу пропустить: ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A_{\textrm {low}}\leq B_{\textrm {high}}}$ ${\displaystyle A_{\textrm {high}}\geq B_{\textrm {low}}}$

• все узлы справа от узлов, нижнее значение которых выходит за пределы заданного интервала.
• все узлы, максимальное значение которых находится ниже начала заданного интервала.

Запросы на членство

Некоторое повышение производительности может быть достигнуто, если дерево избежит ненужных обходов. Они могут возникнуть при добавлении интервалов, которые уже существуют, или удалении интервалов, которые не существуют.

Полный порядок может быть определен на интервалах, упорядочив их сначала по нижним границам, а затем по верхним границам. Затем проверка членства может быть выполнена за время, в отличие от времени, необходимого для поиска дубликатов, если интервалы перекрывают интервал, который нужно вставить или удалить. Преимущество этого решения в том, что оно не требует дополнительных структур. Изменение является строго алгоритмическим. Недостатком является то, что запросы членства занимают время. ${\displaystyle O(\log n)}$ ${\displaystyle O(k+\log n)}$ ${\displaystyle k}$ ${\displaystyle O(\log n)}$

В качестве альтернативы, по скорости памяти, запросы членства в ожидаемом постоянном времени могут быть реализованы с помощью хэш-таблицы, обновляемой в соответствии с деревом интервалов. Это не обязательно удвоит общее требование к памяти, если интервалы хранятся по ссылке, а не по значению. ${\displaystyle O(n)}$

Пример Java: Добавление нового интервала в дерево

Ключом каждого узла является сам интервал, поэтому узлы упорядочены сначала по наименьшему значению, а затем по наибольшему значению, а значение каждого узла является конечной точкой интервала:

public void add ( Interval i ) { put ( i , i.getEnd ( ) ); }      

Пример Java: Поиск точки или интервала в дереве

Для поиска интервала нужно пройти по дереву, используя ключ ( n.getKey()) и высокое значение ( n.getValue()), чтобы исключить любые ветви, которые не могут перекрывать запрос. Простейшим случаем является точечный запрос:

// Поиск всех интервалов, содержащих "p", начиная с узла "n" и добавляя соответствующие интервалы в список "result" public void search ( IntervalNode n , Point p , List < Interval > result ) { // Не искать несуществующие узлы if ( n == null ) return ;               // Если p находится справа от самой правой точки любого интервала // в этом узле и всех дочерних узлах, совпадений не будет. if ( p . compareTo ( n . getValue ()) > 0 ) return ;       // Поиск оставшихся дочерних элементов search ( n.getLeft ( ) , p , result );    // Проверяем этот узел if ( n . getKey (). contains ( p )) result . add ( n . getKey ());    // Если p находится слева от начала этого интервала, // то он не может быть ни в одном дочернем элементе справа. if ( p . compareTo ( n . getKey (). getStart ()) < 0 ) return ;       // В противном случае, поиск правых потомков search ( n.getRight ( ) , p , result ); }   

где

a.compareTo(b)возвращает отрицательное значение, если a < b

a.compareTo(b)возвращает ноль, если a = b

a.compareTo(b)возвращает положительное значение, если a > b

Код для поиска интервала аналогичен, за исключением проверки посередине:

// Проверяем этот узел if ( n . getKey (). acrosssWith ( i )) result . add ( n . getKey ());   

overlapsWith()определяется как:

public boolean acrosssWith ( Interval other ) { return start.compareTo ( other.getEnd ( ) ) < = 0 && end.compareTo ( other.getStart ( ) ) > = 0 ; }​​            

Более высокие измерения

Расширенные деревья могут быть расширены до более высоких измерений путем циклического обхода измерений на каждом уровне дерева. Например, для двух измерений нечетные уровни дерева могут содержать диапазоны для x -координаты, в то время как четные уровни содержат диапазоны для y -координаты. Такой подход эффективно преобразует структуру данных из расширенного бинарного дерева в расширенное kd-дерево , тем самым значительно усложняя алгоритмы балансировки для вставок и удалений.

Более простое решение — использовать вложенные интервальные деревья. Сначала создайте дерево, используя диапазоны для координаты y . Теперь для каждого узла в дереве добавьте еще одно интервальное дерево на x -диапазонах для всех элементов, чей y -диапазон совпадает с y -диапазоном этого узла.

Преимущество этого решения в том, что его можно расширить до произвольного числа измерений, используя ту же кодовую базу.

Сначала дополнительная стоимость вложенных деревьев может показаться непомерной, но обычно это не так. Как и в случае с невложенным решением ранее, на каждую x -координату требуется один узел, что дает одинаковое количество узлов для обоих решений. Единственные дополнительные накладные расходы — это вложенные структуры деревьев, по одному на вертикальный интервал. Эта структура обычно имеет незначительный размер, состоящий только из указателя на корневой узел и, возможно, из числа узлов и глубины дерева.

Медиально- или продольно-ориентированное дерево

Медиальное или ориентированное по длине дерево похоже на расширенное дерево, но симметрично, с бинарным деревом поиска, упорядоченным по срединным точкам интервалов. В каждом узле есть максимально ориентированная двоичная куча , упорядоченная по длине интервала (или половине длины). Также мы храним минимальное и максимальное возможное значение поддерева в каждом узле (отсюда симметрия).

Тест на перекрытие

Используя только начальные и конечные значения двух интервалов , для , тест на перекрытие можно выполнить следующим образом: ${\displaystyle \left(a_{i},b_{i}\right)}$ ${\displaystyle i=0,1}$

${\displaystyle a_{0}<b_{1}}$и ${\displaystyle a_{1}<b_{0}}$

Это можно упростить, используя сумму и разность:

${\displaystyle s_{i}=a_{i}+b_{i}}$

${\displaystyle d_{i}=b_{i}-a_{i}}$

Что сводит тест на перекрытие к следующему:

${\displaystyle \left|s_{1}-s_{0}\right|<d_{0}+d_{1}}$

Добавление интервала

Добавление новых интервалов в дерево происходит так же, как и для двоичного дерева поиска с использованием медиального значения в качестве ключа. Мы перемещаем в двоичную кучу, связанную с узлом, и обновляем минимальное и максимальное возможные значения, связанные со всеми более высокими узлами. ${\displaystyle d_{i}}$

Поиск всех перекрывающихся интервалов

Давайте используем для интервала запроса, а для ключа узла (по сравнению с интервалами) ${\displaystyle a_{q},b_{q},m_{q},d_{q}}$ ${\displaystyle M_{n}}$ ${\displaystyle m_{i}}$

Начиная с корневого узла, в каждом узле мы сначала проверяем, возможно ли, что наш интервал запроса перекрывается с поддеревом узла, используя минимальные и максимальные значения узла (если это не так, мы не продолжаем для этого узла).

Затем мы вычисляем интервалы внутри этого узла (не его дочерних узлов), которые будут перекрываться с интервалом запроса (зная ): ${\displaystyle \min \left\{d_{i}\right\}}$ ${\displaystyle m_{i}=M_{n}}$

${\displaystyle \min \left\{d_{i}\right\}=\left|m_{q}-M_{n}\right|-d_{q}}$

и выполнить запрос к его двоичной куче для ' больше, чем ${\displaystyle d_{i}}$ ${\displaystyle \min \left\{d_{i}\right\}}$

Затем мы проходим по левому и правому дочерним узлам узла, выполняя то же самое.

В худшем случае нам придется сканировать все узлы двоичного дерева поиска, но поскольку двоичный запрос кучи является оптимальным, это приемлемо (двумерная задача не может быть оптимальной в обоих измерениях).

Ожидается, что этот алгоритм будет быстрее традиционного интервального дерева (расширенного дерева) для операций поиска. Добавление элементов на практике немного медленнее, хотя порядок роста тот же.

Ссылки

1. https://personal.us.es/almar/cg/08windowing.pdf ^{[ пустой URL-адрес PDF ]}
2. Йенс М. Шмидт. Задачи интервального закалывания в малых целочисленных диапазонах . DOI. ISAAC'09, 2009
3. Запросы диапазона#Операторы полугруппы

• Марк де Берг , Марк ван Кревельд , Марк Овермарс и Отфрид Шварцкопф . Вычислительная геометрия , второе исправленное издание. Springer-Verlag 2000. Раздел 10.1: Интервальные деревья, стр. 212–217.
• Кормен, Томас Х .; Лейзерсон, Чарльз Э .; Ривест, Рональд Л .; Штейн, Клиффорд (2009), Введение в алгоритмы (3-е изд.), MIT Press и McGraw-Hill, ISBN 978-0-262-03384-8
• Франко П. Препарата и Майкл Ян Шамос . Вычислительная геометрия: Введение . Springer-Verlag, 1985

Внешние ссылки

• CGAL: Библиотека алгоритмов вычислительной геометрии на языке C++, содержащая надежную реализацию Range Trees.
• Boost.Icl предлагает реализации интервальных наборов и карт на языке C++.
• IntervalTree (Python) — центрированное интервальное дерево с балансировкой AVL, совместимое с тегированными интервалами
• Интервальное дерево (C#) — расширенное интервальное дерево с балансировкой AVL
• Дерево интервалов (Ruby) — центрированное дерево интервалов, неизменяемое, совместимое с тегированными интервалами.
• IntervalTree (Java) — расширенное интервальное дерево с балансировкой AVL, поддержкой перекрытия, поиска, интерфейса Collection, интервалов, связанных с идентификатором
• Tree::Interval::Fast (Perl/C) — эффективное создание и обработка интервальных деревьев.