В логике , в частности в дедуктивном рассуждении , аргумент является действительным, если и только если он принимает форму, которая делает невозможным, чтобы предпосылки были истинными , а заключение, тем не менее, ложным . [1] Для действительного аргумента не требуется, чтобы предпосылки были фактически истинными, [2] но чтобы предпосылки были такими, которые, если бы они были истинными, гарантировали бы истинность заключения аргумента. Действительные аргументы должны быть четко выражены с помощью предложений, называемых правильно сформированными формулами (также называемыми wffs или просто формулами ).
Обоснованность аргумента может быть проверена, доказана или опровергнута и зависит от его логической формы . [3]
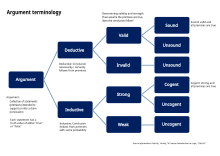
В логике аргумент — это набор взаимосвязанных утверждений, выражающих посылки (которые могут состоять из неэмпирических доказательств, эмпирических доказательств или содержать некоторые аксиоматические истины) и необходимый вывод, основанный на взаимосвязи посылок.
Аргумент является действительным , если и только если было бы противоречиво, чтобы заключение было ложным, если все посылки истинны. [3] Действительность не требует истинности посылок, вместо этого она просто требует , чтобы заключение следовало из посылок, не нарушая правильности логической формы . Если также доказано, что посылки действительного аргумента истинны, то он считается обоснованным . [3]
Соответствующее условие действительного аргумента является логической истиной , а отрицание его соответствующего условия является противоречием . Заключение является необходимым следствием своих посылок.
Аргумент, который не является действительным, называется «недействительным».
Примером обоснованного (и обоснованного ) аргумента является следующий известный силлогизм :
То, что делает этот аргумент действительным, не то, что он имеет истинные предпосылки и истинное заключение. Действительность касается связи между двумя предпосылками, необходимости заключения. Должна быть установлена связь между предпосылками, т. е. средний термин между предпосылками. Если у вас есть только две несвязанные предпосылки, то аргумента нет. Обратите внимание, что некоторые термины повторяются: men — это вариация man в посылках один и два, Socrates и термин mortal повторяются в заключении. Аргумент был бы таким же действительным, если бы и предпосылки, и заключение были ложными. Следующий аргумент имеет ту же логическую форму , но с ложными предпосылками и ложным заключением, и он в равной степени действителен:
Независимо от того, как может быть устроена вселенная, никогда не может быть так, чтобы эти аргументы оказались одновременно истинными посылками, но ложным выводом. Вышеуказанные аргументы можно противопоставить следующему недействительному:
В этом случае вывод противоречит дедуктивной логике предыдущих посылок, а не выводится из нее. Следовательно, аргумент логически «недействителен», даже если вывод можно считать «истинным» в общих чертах. Посылка «Все люди бессмертны» также считалась бы ложной вне рамок классической логики. Однако в этой системе «истинно» и «ложно» по сути функционируют скорее как математические состояния, такие как двоичные 1 и 0, чем как философские концепции, обычно связанные с этими терминами. Формальные аргументы, которые являются недействительными, часто связаны по крайней мере с одним заблуждением, которое должно быть проверяемым.
Стандартная точка зрения заключается в том, что обоснованность аргумента зависит от его логической формы. Логики используют множество методов для представления логической формы аргумента. Простой пример, примененный к двум из приведенных выше иллюстраций, выглядит следующим образом: пусть буквы «P», «Q» и «S» обозначают, соответственно, множество людей, множество смертных и Сократа. Используя эти символы, первый аргумент можно сократить следующим образом:
Аналогично третий аргумент становится следующим:
Аргумент называется формально допустимым, если он обладает структурной самосогласованностью, то есть если, когда все операнды между посылками истинны, выведенное заключение всегда также истинно. В третьем примере исходные посылки не могут логически привести к заключению и поэтому классифицируются как недопустимый аргумент.
Формула формального языка является допустимой формулой тогда и только тогда, когда она истинна при любой возможной интерпретации языка. В пропозициональной логике они являются тавтологиями .
Утверждение может быть названо действительным, т.е. логической истиной, в некоторых системах логики, например, в модальной логике, если утверждение истинно во всех интерпретациях. В аристотелевской логике утверждения не являются действительными сами по себе. Действительность относится ко всем аргументам. То же самое верно и в пропозициональной логике (утверждения могут быть истинными или ложными, но не могут называться действительными или недействительными).
На действительность дедукции не влияет истинность предпосылки или истинность заключения. Следующий вывод совершенно действителен:
Проблема с аргументом в том, что он не является обоснованным . Для того чтобы дедуктивный аргумент был обоснованным, аргумент должен быть действительным , а все посылки должны быть истинными. [3]
Теория моделей анализирует формулы относительно определенных классов интерпретации в подходящих математических структурах. В этом прочтении формула действительна, если все такие интерпретации делают ее истинной. Вывод действителен, если все интерпретации, которые подтверждают предпосылки, подтверждают заключение. Это известно как семантическая валидность . [4]
В действительности, сохраняющей истину, интерпретация, при которой всем переменным присваивается значение истинности «истина», создает значение истинности «истина».
В сохраняющей ложь валидности интерпретация, при которой всем переменным присваивается истинностное значение «ложь», создает истинностное значение «ложь». [5]