Капиллярное давление

Давление между двумя жидкостями от сил между жидкостями и стенками трубки

В статике жидкости капиллярное давление ( ) — это давление между двумя несмешивающимися жидкостями в тонкой трубке (см. капиллярное действие ), возникающее в результате взаимодействия сил между жидкостями и твердыми стенками трубки. Капиллярное давление может служить как противодействующей, так и движущей силой для транспортировки жидкости и является важным свойством для исследовательских и промышленных целей (а именно микрофлюидного проектирования и добычи нефти из пористой породы). Оно также наблюдается в природных явлениях. ${\displaystyle {p_{c}}}$

Определение

Примеры различных условий смачивания при соответствующих углах контакта

Капиллярное давление определяется как:

${\displaystyle p_{c}=p_{\text{non-wetting phase}}-p_{\text{wetting phase}}}$

где:

${\displaystyle p_{\text{c}}}$капиллярное давление

${\displaystyle p_{\text{non-wetting phase}}}$давление несмачивающей фазы

${\displaystyle p_{\text{wetting phase}}}$давление смачивающей фазы

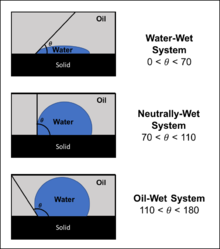
Фаза смачивания определяется по ее способности преимущественно диффундировать через стенки капилляров перед несмачивающей фазой. «Смачиваемость» жидкости зависит от ее поверхностного натяжения, сил, которые заставляют жидкость занимать минимально возможное пространство, и определяется углом контакта жидкости. ^[1] «Смачиваемость» жидкости можно контролировать, изменяя свойства капиллярной поверхности ( например, шероховатость, гидрофильность). Однако в системах масло-вода смачивающей фазой обычно является вода , тогда как в системах газ-нефть смачивающей фазой обычно является масло. ^[1] Независимо от системы, на результирующем изогнутом интерфейсе между двумя жидкостями возникает разность давлений. ^[2]

Уравнения

Формулы капиллярного давления выводятся из соотношения давления между двумя жидкими фазами в капиллярной трубке в состоянии равновесия, которое заключается в том, что сила вверх = сила вниз. Эти силы описываются как: ^[1]

${\displaystyle {\text{force up = interfacial tension of the fluid(s) acting along the perimeter of the capillary tube}}}$

${\displaystyle {\text{force down = (density gradient difference) x (cross-sectional area) x (height of the capillary rise in the tube)}}}$

Эти силы можно описать с помощью межфазного натяжения и угла контакта жидкостей, а также радиуса капиллярной трубки. Интересное явление, капиллярный подъем воды (как показано справа), дает хороший пример того, как эти свойства объединяются, чтобы управлять потоком через капиллярную трубку, и как эти свойства измеряются в системе. Существуют два общих уравнения, которые описывают соотношение силы вверх и силы вниз двух жидкостей в равновесии.

Схема капиллярного подъема воды для демонстрации измерений, используемых в уравнении Юнга-Лапласа

Уравнение Юнга–Лапласа описывает капиллярное давление с помощью силы и является наиболее часто используемой вариацией уравнения капиллярного давления: ^{[2] [1]}

${\displaystyle p_{c}={\frac {2\gamma \cos \theta }{r_{c}}}}$

где:

${\displaystyle \gamma }$это межфазное натяжение

${\displaystyle r}$эффективный радиус интерфейса

${\displaystyle \theta }$это краевой угол смачивания жидкости на поверхности капилляра

Формула силы прижатия для капиллярного давления выглядит следующим образом: ^[1]

${\displaystyle p_{c}={\frac {\pi r^{2}h(\Gamma _{w}-\Gamma _{nw})}{\pi r^{2}}}=h(\Gamma _{w}-\Gamma _{nw})}$

где:

${\displaystyle h}$это высота капиллярного подъема

${\displaystyle \Gamma _{w}}$градиент плотности смачивающей фазы

${\displaystyle \Gamma _{nw}}$градиент плотности несмачивающей фазы

Приложения

Микрофлюидика

Микрофлюидика — это изучение и проектирование управления или транспортировки небольших объемов потока жидкости через пористый материал или узкие каналы для различных применений ( например, смешивание, разделение). Капиллярное давление — одна из многих характеристик, связанных с геометрией, которые можно изменять в микрофлюидном устройстве для оптимизации определенного процесса. Например, при увеличении капиллярного давления смачиваемая поверхность в канале будет тянуть жидкость через трубопровод. Это устраняет необходимость в насосе в системе и может сделать желаемый процесс полностью автономным. Капиллярное давление также можно использовать для блокировки потока жидкости в микрофлюидном устройстве.

Схема протекания жидкости через микрофлюидное устройство под действием капилляров (см. изображение капиллярного подъема воды для левого и правого контактных углов в микрофлюидных каналах)

Капиллярное давление в микроканале можно описать как:

${\displaystyle p_{c}=-\gamma \left({\frac {cos\theta _{b}+cos\theta _{t}}{d}}+{\frac {cos\theta _{l}+cos\theta _{r}}{w}}\right)}$

где:

${\displaystyle {\gamma }}$поверхностное натяжение жидкости

${\displaystyle {\theta _{b}}}$это угол контакта в нижней части

${\displaystyle {\theta _{t}}}$это угол контакта в верхней части

${\displaystyle {\theta _{l}}}$угол контакта на левой стороне канала

${\displaystyle {\theta _{r}}}$это контактные углы на правой стороне канала

${\displaystyle {d}}$это глубина

${\displaystyle {w}}$это ширина

Таким образом, капиллярное давление может быть изменено путем изменения поверхностного натяжения жидкости, контактных углов жидкости или глубины и ширины каналов устройства. Чтобы изменить поверхностное натяжение, можно нанести поверхностно-активное вещество на стенки капилляров. Контактные углы изменяются при внезапном расширении или сжатии внутри каналов устройства. Положительное капиллярное давление представляет собой клапан на потоке жидкости, тогда как отрицательное давление представляет собой жидкость, втягиваемую в микроканал. ^[3]

Методы измерения

Методы проведения физических измерений капиллярного давления в микроканале не были тщательно изучены, несмотря на необходимость точных измерений давления в микрофлюидике. Основная проблема с измерением давления в микрофлюидных устройствах заключается в том, что объем жидкости слишком мал для использования в стандартных инструментах измерения давления. В некоторых исследованиях было представлено использование микробаллонов, которые являются датчиками давления, изменяющими размер. Сервообнуление, которое исторически использовалось для измерения артериального давления, также было продемонстрировано для предоставления информации о давлении в микрофлюидных каналах с помощью системы управления LabVIEW. По сути, микропипетка погружается в жидкость микроканала и программируется на реагирование на изменения в мениске жидкости. Смещение в мениске жидкости в микропипетке вызывает падение напряжения, которое запускает насос для восстановления исходного положения мениска. Давление, оказываемое насосом, интерпретируется как давление внутри микроканала. ^[4]

Примеры

Текущие исследования в области микрофлюидики сосредоточены на разработке диагностики в месте оказания помощи и методов сортировки клеток (см. lab-on-a-chip ), а также на понимании поведения клеток ( например, рост клеток, старение клеток). В области диагностики тест бокового потока является распространенной платформой микрофлюидных устройств, которая использует капиллярные силы для перемещения жидкости через пористую мембрану. Самым известным тестом бокового потока является домашний тест на беременность , в котором телесная жидкость сначала смачивает, а затем протекает через пористую мембрану, часто целлюлозу или стекловолокно, достигая линии захвата, чтобы указать на положительный или отрицательный сигнал. Преимуществом этой конструкции и нескольких других микрофлюидных устройств является ее простота (например, отсутствие вмешательства человека во время работы) и низкая стоимость. Однако недостатком этих тестов является то, что капиллярное действие невозможно контролировать после его начала, поэтому время теста нельзя ускорить или замедлить (что может создать проблему, если во время потока жидкости должны происходить определенные зависящие от времени процессы). ^[5]

Другим примером работы в месте оказания помощи, включающей компонент дизайна, связанный с капиллярным давлением, является отделение плазмы от цельной крови путем фильтрации через пористую мембрану. Эффективное и объемное отделение плазмы от цельной крови часто необходимо для диагностики инфекционных заболеваний, например, для теста на вирусную нагрузку ВИЧ. Однако эта задача часто выполняется с помощью центрифугирования, что ограничивается клиническими лабораторными условиями. Примером этого устройства фильтрации в месте оказания помощи является фильтр с насадочным слоем, который продемонстрировал способность отделять плазму от цельной крови, используя асимметричные капиллярные силы в порах мембраны. ^[6]

Нефтехимическая промышленность

Капиллярное давление играет жизненно важную роль в извлечении подземных углеводородов (таких как нефть или природный газ) из-под пористых пород-коллекторов. Его измерения используются для прогнозирования насыщенности пластовой жидкостью и емкости покрышки-порода, а также для оценки данных относительной проницаемости (способности жидкости транспортироваться в присутствии второй несмешивающейся жидкости). ^[7] Кроме того, было показано, что капиллярное давление в пористых породах влияет на фазовое поведение пластовых жидкостей, тем самым влияя на методы извлечения и восстановления. ^[8] Крайне важно понимать эти геологические свойства пласта для его разработки, добычи и управления ( например, насколько легко извлекать углеводороды).

Пожар на буровой установке Deepwater Horizon в 2010 году

^{[ сомнительно – обсудить ]} Разлив нефти Deepwater Horizon является примером того, почему капиллярное давление имеет важное значение для нефтехимической промышленности . Считается, что после взрыва нефтяной платформы Deepwater Horizon в Мексиканском заливе в 2010 году метановый газ прорвался через недавно установленную герметизацию и расширился вверх и из платформы. Хотя исследования капиллярного давления (или потенциальное отсутствие таковых) не обязательно лежат в основе этого конкретного разлива нефти, измерения капиллярного давления дают важную информацию для понимания свойств резервуара, которые могли повлиять на инженерные решения, принятые в случае с Deepwater Horizon. ^[9]

Капиллярное давление, как это видно в нефтяной инженерии, часто моделируется в лаборатории, где оно регистрируется как давление, необходимое для вытеснения некоторой смачивающей фазы несмачивающей фазой для установления равновесия. ^[10] Для справки, капиллярное давление между воздухом и рассолом (что является важной системой в нефтехимической промышленности), как было показано, находится в диапазоне от 0,67 до 9,5 МПа. ^[11] Существуют различные способы прогнозирования, измерения или расчета отношений капиллярного давления в нефтегазовой промышленности. К ним относятся следующие: ^[7]

J-функция Леверета

J-функция Леверетта служит для установления связи между капиллярным давлением и структурой пор (см. J-функция Леверетта ).

Инъекция ртути

Схема метода впрыскивания ртути для измерения капиллярного давления: 1. Высушенный образец откачивается, 2. Добавляется ртуть, 3. Система открывается до атмосферного давления, уровень ртути падает, 4. Давление резко увеличивается, так что ртуть попадает в поры образца.

Кривая капиллярного давления, полученная методом впрыскивания ртути.

Этот метод хорошо подходит для нерегулярных образцов горных пород ( например, тех, которые находятся в буровом шламе) и обычно используется для понимания связи между капиллярным давлением и пористой структурой образца. ^[12] В этом методе поры образца горной породы откачиваются, после чего поры заполняются ртутью с возрастающим давлением. Между тем, объем ртути при каждом заданном давлении регистрируется и представляется как распределение размеров пор или преобразуется в соответствующие данные по нефти/газу. Одним из недостатков этого метода является то, что он не учитывает взаимодействия жидкости с поверхностью. Однако весь процесс инъекции ртути и сбора данных происходит быстро по сравнению с другими методами. ^[7]

Метод пористой пластины

Метод пористой пластины — это точный способ понять соотношение капиллярного давления в системах жидкость-воздух. В этом процессе образец, насыщенный водой, помещается на плоскую пластину, также насыщенную водой, внутри газовой камеры. Газ впрыскивается при возрастающем давлении, таким образом вытесняя воду через пластину. Давление газа представляет собой капиллярное давление, а количество воды, выброшенной из пористой пластины, коррелирует с водонасыщенностью образца. ^[7]

Метод центрифуги

Метод центрифуги основан на следующем соотношении между капиллярным давлением и силой тяжести: ^[7]

Упрощенная схема центрифужной установки для измерения капиллярного давления системы рассол-нефть

${\displaystyle p_{c}=hg(\rho _{w}-\rho _{nw})}$

где:

${\displaystyle h}$это высота капиллярного подъема

${\displaystyle g}$это гравитация

${\displaystyle \rho _{w}}$плотность смачивающей фазы

${\displaystyle \rho _{nw}}$плотность несмачивающей фазы

Центробежная сила по сути служит в качестве приложенного капиллярного давления для небольших испытательных пробок, часто состоящих из рассола и нефти. В процессе центрифугирования заданное количество рассола вытесняется из пробки при определенных центробежных скоростях вращения. Стеклянная пробирка измеряет количество жидкости по мере ее вытеснения, и эти показания приводят к кривой, которая связывает скорости вращения с объемами дренажа. Скорость вращения коррелирует с капиллярным давлением с помощью следующего уравнения:

${\displaystyle p_{c}=7.9e^{-8}(\rho _{1}-\rho _{2})\omega ^{2}(r_{b}^{2}-r_{t}^{2})}$

где:

${\displaystyle r_{b}}$радиус вращения нижней части образца керна

${\displaystyle r_{t}}$радиус вращения верхней части образца керна

${\displaystyle \omega }$это скорость вращения

Основными преимуществами этого метода являются его быстрота (получение кривых за несколько часов) и отсутствие ограничений на выполнение при определенных температурах. ^[13]

Другие методы включают метод давления пара, метод гравитационного равновесия, динамический метод, полудинамический метод и переходный метод.

Корреляции

В дополнение к измерению капиллярного давления в лабораторных условиях для моделирования давления в нефтяном/газовом резервуаре, существует несколько соотношений для описания капиллярного давления с учетом конкретных условий породы и добычи. Например, RH Brooks и AT Corey разработали соотношение для капиллярного давления во время дренирования нефти из пористой среды, насыщенной нефтью, в которую проникает газ: ^[14]

${\displaystyle p_{cgo}=p_{t}({\frac {1-S_{or}}{S_{o}-S_{or}}})^{(1/\lambda )}}$

где:

${\displaystyle P_{cgo}}$капиллярное давление между нефтяной и газовой фазами

${\displaystyle S_{o}}$это насыщенность нефтью

${\displaystyle S_{or}}$это остаточная нефтенасыщенность, которая остается в порах при высоком капиллярном давлении

${\displaystyle P_{t}}$пороговое давление (давление, при котором допускается течение газовой фазы)

${\displaystyle \lambda }$это параметр, который связан с распределением размеров пор

${\displaystyle \lambda >2}$для узких распределений

${\displaystyle \lambda <2}$для широкого распространения

Кроме того, Р. Г. Бентсен и Дж. Анли разработали корреляцию для капиллярного давления во время дренажа из пористого образца породы, в котором нефтяная фаза вытесняет насыщенную воду: ^[15]

${\displaystyle p_{cow}=p_{t}-p_{cs}ln({\frac {S_{w}-S_{wi}}{1-S_{wi}}})}$

где:

${\displaystyle P_{cow}}$капиллярное давление между нефтяной и водной фазами

${\displaystyle P_{cs}}$параметр, который управляет формой функции капиллярного давления

${\displaystyle ({\frac {S_{w}-S_{wi}}{1-S_{wi}}})}$нормализованная насыщенность смачивающей фазы

${\displaystyle S_{w}}$насыщенность смачивающей фазы

${\displaystyle S_{wi}}$является неснижаемой насыщенностью смачивающей фазы

Усреднение кривых капиллярного давления и водонасыщенности

Было показано, что поскольку симуляторы резервуаров используют данные о капиллярном давлении первичного дренажа для расчетов моделирования высоты насыщения, данные о капиллярном давлении первичного дренажа должны быть усреднены таким же образом, как усредняются водонасыщенности. Кроме того, поскольку симуляторы резервуаров используют данные о капиллярном давлении впитывания и вторичного дренажа для расчетов вытеснения жидкостей, эти капиллярные давления не должны быть усреднены, как данные о капиллярном давлении первичного дренажа. Их можно усреднить с помощью J-функции Леверетта . Уравнения усреднения следующие ^[16]

усреднение первичного дренажного капиллярного давления в сравнении с нормализованными данными насыщения

${\displaystyle {\text{average Pc}}={\frac {\sum _{i=1}^{n}\left({\phi V_{\mathit {b}}P_{\mathit {c}}}\right)_{i}}{\sum _{i=1}^{n}\left({\phi V_{\mathit {b}}}\right)_{i}}}}$

где — количество образцов керна, — эффективная пористость, — общий объем образца, — данные о первичном дренажном капиллярном давлении в зависимости от нормализованной водонасыщенности. ${\displaystyle n}$ ${\displaystyle \phi }$ ${\displaystyle Vb}$ ${\displaystyle Pc}$

усреднение капиллярного давления впитывания и вторичного дренажа по сравнению с нормализованными данными насыщения

${\displaystyle {\text{average Pc}}={\frac {\sum _{i=1}^{n}\left({\frac {P_{\mathit {c}}{\sqrt {k/\phi }}}{\gamma }}\right)_{i}}{\sum _{i=1}^{n}\left({\frac {\sqrt {k/\phi }}{\gamma }}\right)_{i}}}}$

где - количество образцов керна, - эффективная пористость, - абсолютная проницаемость, - межфазное натяжение или IFT, и - данные капиллярного давления впитывания или вторичного дренажа в зависимости от нормализованной водонасыщенности. ${\displaystyle n}$ ${\displaystyle \phi }$ ${\displaystyle k}$ ${\displaystyle \gamma }$ ${\displaystyle Pc}$

В природе

Игольчатый лед

Изображение игольчатого льда

Помимо того, что капиллярное давление используется в медицинских и энергетических целях, оно также является причиной различных природных явлений. Например, игольчатый лед , наблюдаемый в холодной почве, возникает из-за капиллярного действия . Первые крупные вклады в изучение игольчатого льда или просто морозного пучения были сделаны Стивеном Табером (1929) и Гуннаром Бесковым (1935), которые независимо друг от друга стремились понять замерзание почвы. Первоначальная работа Табера была связана с пониманием того, как размер пор в почве влияет на величину морозного пучения. Он также обнаружил, что морозное пучение благоприятно для роста кристаллов и что градиент натяжения почвенной влаги направляет воду вверх к фронту промерзания вблизи верхней части земли. ^[17] В своих исследованиях Бесков определил это натяжение почвенной влаги как «капиллярное давление» (а почвенную воду как «капиллярную воду»). Бесков определил, что тип почвы и эффективное напряжение на частицах почвы влияют на морозное пучение, где эффективное напряжение представляет собой сумму давления сверху земли и капиллярного давления. ^[18]

В 1961 году Д. Х. Эверетт подробно остановился на исследованиях Табера и Бескова, чтобы понять, почему поры, заполненные льдом, продолжают расти. Он использовал принципы термодинамического равновесия, модель поршневого цилиндра для роста льда и следующее уравнение для понимания замерзания воды в пористой среде (непосредственно применимое к образованию игольчатого льда):

Модель поршневого цилиндра для нарастания льда

${\displaystyle P_{s}-P_{l}=\Psi _{sl}{\frac {dA_{r}}{dV}}=\Psi _{sl}{\tilde {K}}}$

где:

${\displaystyle {P_{s}}}$это давление твердого кристалла

${\displaystyle {P_{l}}}$это давление в окружающей жидкости

${\displaystyle {\Psi _{sl}}}$это межфазное натяжение между твердым телом и жидкостью

${\displaystyle {A_{r}}}$площадь поверхности границы раздела фаз

${\displaystyle {V}}$объем кристалла

${\displaystyle {\tilde {K}}}$это средняя кривизна границы раздела твердое тело/жидкость

С помощью этого уравнения и модели Эверетт отметил поведение воды и льда при различных условиях давления на границе раздела твердое тело-жидкость. Эверетт определил, что если давление льда равно давлению жидкости под поверхностью, рост льда не может продолжаться в капилляре. Таким образом, при дополнительной потере тепла для воды наиболее благоприятно перемещаться вверх по капилляру и замерзать в верхнем цилиндре (поскольку игольчатый лед продолжает расти поверх себя над поверхностью почвы). По мере увеличения давления льда возникает изогнутая граница раздела между твердым телом и жидкостью, и лед либо растает, либо равновесие будет восстановлено, так что дальнейшая потеря тепла снова приведет к образованию льда. В целом Эверетт определил, что вспучивание при замерзании (аналогично развитию игольчатого льда) происходит как функция размера пор в почве и энергии на границе раздела льда и воды. К сожалению, недостатком модели Эверетта является то, что он не учитывал влияние частиц почвы на поверхность. ^{[19] [20]}

Кровеносная система

Капилляры в кровеносной системе жизненно важны для обеспечения питательными веществами и выведения отходов по всему телу. В капиллярах существуют градиенты давления (из-за гидростатического и онкотического давления ), которые контролируют кровоток на уровне капилляров и в конечном итоге влияют на процессы капиллярного обмена ( например, поток жидкости). ^[21] Из-за ограничений в технологии и структуре тела большинство исследований капиллярной активности проводятся в сетчатке, губах и коже, исторически с помощью канюляции или системы сервообнуления. Капилляроскопия использовалась для визуализации капилляров в коже в 2D, и, как сообщается, наблюдался средний диапазон капиллярного давления от 10,5 до 22,5 мм рт. ст. у людей и повышение давления у людей с диабетом 1 типа и гипертонией . По сравнению с другими компонентами кровеносной системы капиллярное давление низкое, чтобы избежать разрыва, но достаточное для облегчения капиллярных функций. ^[22]

Смотрите также

• Капиллярное действие
• Капиллярное число
• Расклинивающее давление
• J-функция Леверета
• Уравнение Юнга-Лапласа
• Давление Лапласа
• Поверхностное натяжение
• Микрофлюидика
• Кривая_удержания_воды
• ТЕМ-функция
• Индекс смачиваемости USBM

Ссылки

1. Fanchi, John R.. (2006). Принципы прикладного моделирования пласта (3-е издание). Elsevier.
2. Tiab, Donaldson, Djebbar, Erle C. (2004). Петрофизика - Теория и практика измерения свойств пластовых пород и переноса флюидов (2-е изд.).{{cite book}}: CS1 maint: multiple names: authors list (link)
3. Юнкер, Д. (2002). Капиллярные микрофлюидные системы для био/химии .
4. Грундманн, Клавика, Ландольт, Барретт, Вебер, Обрист, А, Ф, А, М, Б, Д (25 октября 2015 г.). "ИЗМЕРЕНИЕ ДАВЛЕНИЯ ЖИДКОСТИ В МИКРОКАНАЛАХ". Международная конференция по миниатюрным системам для химии и наук о жизни .{{cite journal}}: CS1 maint: multiple names: authors list (link)
5. Саджида, Кавдеа, Даудк, Мухаммад, Абдель-Нассер, Мухаммад (2015). «Конструкции, форматы и применение анализа бокового потока: обзор литературы». Журнал Саудовского химического общества . 19 (6): 689–705. doi : 10.1016/j.jscs.2014.09.001 .{{cite journal}}: CS1 maint: multiple names: authors list (link)
6. Ли, Ан, КК, Ч. Х. (2013). «Новый сепаратор цельной крови/плазмы на чипе, управляемый асимметричными капиллярными силами». Lab on a Chip . 13 (16): 3261–7. doi :10.1039/c3lc50370d. PMID  23793507.{{cite journal}}: CS1 maint: multiple names: authors list (link)
7. Гловер, Пол. Заметки к курсу магистратуры «Формирование и оценка» . С. 84–94.
8. Nojabaei, Siripatrachai, Johns, Ertekin, B, N, RT, T (ноябрь 2016 г.). «Влияние большого капиллярного давления газа и нефти на добычу: состав черной нефти с расширенным составом». Journal of Petroleum Science and Engineering . 147 : 317–329. doi : 10.1016/j.petrol.2016.05.048 .{{cite journal}}: CS1 maint: multiple names: authors list (link)
9. Палларди, Ричард (9 мая 2016 г.). «Нефтяной разлив Deepwater Horizon 2010 года». Britannica . Получено 7 марта 2017 г. .
10. Тиаб, Джеббар Дональдсон, Эрл К.. (2004). Петрофизика - Теория и практика измерения свойств пластовых пород и переноса флюидов (2-е издание). Elsevier.
11. Melrose, JC (1990, 1 февраля). Valid Capillary Pressure Data at Low Wetting-Phase Saturations (включая связанные статьи 21480 и 21618). Society of Petroleum Engineers. doi:10.2118/18331-PA
12. Purcell, WR 1949. Капиллярные давления — их измерение с помощью ртути и расчет проницаемости на их основе. J Pet Technol 1 (2): 39-48. SPE-949039-G.
13. "Основы течения жидкости в пористых средах: Глава 2. Свойства многофазных насыщенных пород: Лабораторное измерение капиллярного давления: Центробежный метод". PERM Inc.
14. Брукс, Р. Х. и Кори, А. Т. 1964. Гидравлические свойства пористых сред. Статья по гидрологии № 3, Университет штата Колорадо, Форт-Коллинз, Колорадо, 22–27.
15. Бентсен, Р. Г. и Анли, Дж. (1 февраля 1977 г.). Использование методов оценки параметров для преобразования данных центрифуги в кривую капиллярного давления. Общество инженеров-нефтяников. doi:10.2118/5026-PA
16. Мирзаи-Пайаман, А.; Ганбарян, Б. (2021). «Новая методология группировки и усреднения кривых капиллярного давления для моделей резервуаров». Energy Geoscience . 2 (1): 52–62. doi : 10.1016/j.engeos.2020.09.001 . S2CID  225017100.
17. Табер, С. (1930) Механика пучения при замерзании. Журнал геологии, т. 38, стр. 303-317. В Исторических перспективах исследований пучения при замерзании, Лаборатория исследований и инжиниринга холодных регионов США, Специальный отчет 91-23, стр. 29-35.
18. Бесков, Г. (1935) Замерзание грунта и морозное пучение со специальными приложениями к дорогам и железным дорогам. Шведское геологическое общество, C, № 375, Ежегодник № 3 (перевод Дж. О. Остерберга). В Исторических перспективах исследований морозного пучения, Лаборатория исследований и инжиниринга холодных регионов США, Специальный отчет 91-23, стр. 41-157.
19. Эверетт, Д. Х. (1961). «Термодинамика повреждения пористых твердых тел от замерзания». Труды Фарадейского общества . 57 : 1541–1551. doi : 10.1039/tf9615701541.
20. Генри, Карен С. (сентябрь 2000 г.). «Обзор термодинамики вспучивания грунта при замерзании». {{cite journal}}: Цитировать журнал требует |journal=( помощь )
21. Клабунде, Ричард. «Гидростатическое и онкотическое давление». Концепции сердечно-сосудистой физиологии .
22. Шор, Анджела С. (2000). «Капилляроскопия и измерение капиллярного давления». British Journal of Clinical Pharmacology . 50 (6): 501–513. doi : 10.1046 /j.1365-2125.2000.00278.x. PMC 2015012. PMID  11136289.