
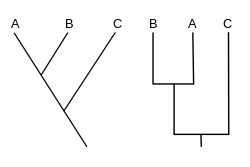
Кладограмма (от греч. clados «ветвь» и gramma «характер») — это диаграмма, используемая в кладистике для отображения отношений между организмами. Однако кладограмма не является эволюционным деревом , поскольку она не показывает, как предки связаны с потомками, и не показывает, насколько они изменились, поэтому многие различные эволюционные деревья могут соответствовать одной и той же кладограмме. [1] [2] [3] [4] [5] Кладограмма использует линии, которые ответвляются в разных направлениях, заканчиваясь на кладе , группе организмов с последним общим предком . Существует много форм кладограмм, но все они имеют линии, которые ответвляются от других линий. Линии можно проследить до того места, где они ответвляются. Эти точки ответвления представляют собой гипотетического предка (не фактическую сущность), который, как можно предположить, демонстрирует черты, общие для терминальных таксонов выше него. [4] [6] Этот гипотетический предок мог бы затем предоставить подсказки о порядке эволюции различных признаков, адаптации и других эволюционных повествованиях о предках. Хотя традиционно такие кладограммы создавались в основном на основе морфологических признаков, данные секвенирования ДНК и РНК и вычислительная филогенетика теперь очень часто используются при создании кладограмм, как сами по себе, так и в сочетании с морфологией.
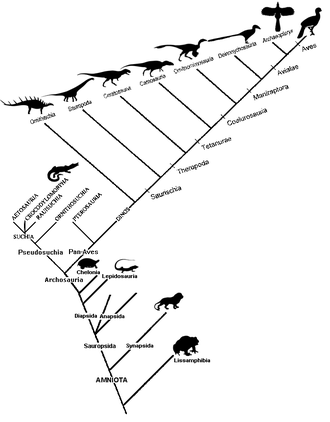
Характеристики, используемые для создания кладограммы, можно грубо разделить на морфологические (синапсидный череп, теплокровные, хорда , одноклеточные и т. д.) или молекулярные (ДНК, РНК или другая генетическая информация). [7] До появления секвенирования ДНК кладистический анализ в основном использовал морфологические данные. Поведенческие данные (для животных) также могут быть использованы. [8]
Поскольку секвенирование ДНК стало дешевле и проще, молекулярная систематика стала все более популярным способом выведения филогенетических гипотез. [9] Использование критерия экономии — лишь один из нескольких методов выведения филогении из молекулярных данных. Такие подходы, как максимальное правдоподобие , которые включают явные модели эволюции последовательностей, являются нехенниговскими способами оценки данных последовательностей. Другим мощным методом реконструкции филогений является использование геномных ретротранспозонных маркеров , которые, как считается, менее подвержены проблеме реверсии , которая преследует данные последовательностей. Также обычно предполагается, что у них низкая частота гомоплазий, поскольку когда-то считалось, что их интеграция в геном была полностью случайной; однако, по крайней мере иногда, это не так.

Исследователи должны решить, какие состояния характера являются «предковыми» ( плезиоморфии ), а какие — производными ( синапоморфии ), поскольку только синапоморфные состояния характера предоставляют доказательства группировки. [10] Это определение обычно делается путем сравнения с состояниями характера одной или нескольких внешних групп . Состояния, общие для внешней группы и некоторых членов внутренней группы, являются симплезиоморфиями; состояния, которые присутствуют только в подмножестве внутренней группы, являются синапоморфиями. Обратите внимание, что состояния характера, уникальные для одного терминала (аутапоморфии), не предоставляют доказательств группировки. Выбор внешней группы является решающим шагом в кладистическом анализе, поскольку различные внешние группы могут создавать деревья с совершенно разной топологией.
Гомоплазия — это состояние признака, которое разделяют два или более таксонов по какой-то причине, отличной от общего происхождения. [11] Двумя основными типами гомоплазии являются конвергенция (эволюция «одного и того же» признака по крайней мере в двух различных линиях) и реверсия (возврат к состоянию предкового признака). Признаки, которые явно гомопластичны, такие как белый мех в разных линиях арктических млекопитающих, не должны включаться в качестве признака в филогенетический анализ, поскольку они не вносят никакого вклада в наше понимание взаимоотношений. Однако гомоплазия часто не очевидна при осмотре самого признака (как, например, в последовательности ДНК), а затем обнаруживается по его несоответствию (неэкономному распределению) на наиболее экономной кладограмме. Обратите внимание, что признаки, которые являются гомопластичными, все еще могут содержать филогенетический сигнал . [12]
Известным примером гомоплазии, вызванной конвергентной эволюцией, является признак «наличие крыльев». Хотя крылья птиц, летучих мышей и насекомых выполняют одну и ту же функцию, каждое из них развивалось независимо, как можно увидеть по их анатомии . Если бы птица, летучая мышь и крылатое насекомое были оценены по признаку «наличие крыльев», гомоплазия была бы введена в набор данных, и это потенциально могло бы запутать анализ, возможно, приведя к ложной гипотезе о родственных связях. Конечно, единственная причина, по которой гомоплазия распознается в первую очередь, заключается в том, что существуют другие признаки, которые подразумевают модель родственных связей, раскрывающую ее гомопластическое распределение.
Кладограмма — это схематический результат анализа, который группирует таксоны на основе только синапоморфий. Существует много других филогенетических алгоритмов, которые обрабатывают данные несколько иначе и приводят к филогенетическим деревьям, которые выглядят как кладограммы, но не являются кладограммами. Например, фенетические алгоритмы, такие как UPGMA и Neighbor-Joining, группируют по общему сходству и рассматривают как синапоморфии, так и симплезиоморфии как доказательство группировки. Полученные диаграммы являются фенограммами, а не кладограммами. Аналогично, результаты методов, основанных на моделях (подходы максимального правдоподобия или байесовский подход), которые учитывают как порядок ветвления, так и «длину ветви», учитывают как синапоморфии, так и аутапоморфии как доказательство за или против группировки. Диаграммы, полученные в результате такого анализа, также не являются кладограммами. [13]
Существует несколько алгоритмов для определения «лучшей» кладограммы. [14] Большинство алгоритмов используют метрику для измерения того, насколько кладограмма-кандидат соответствует данным. Большинство алгоритмов кладограмм используют математические методы оптимизации и минимизации.
В общем случае алгоритмы генерации кладограмм должны быть реализованы в виде компьютерных программ, хотя некоторые алгоритмы можно выполнять вручную, если наборы данных невелики (например, всего несколько видов и несколько характеристик).
Некоторые алгоритмы полезны только тогда, когда характерные данные являются молекулярными (ДНК, РНК); другие алгоритмы полезны только тогда, когда характерные данные являются морфологическими. Другие алгоритмы могут использоваться, когда характерные данные включают как молекулярные, так и морфологические данные.
Алгоритмы для кладограмм или других типов филогенетических деревьев включают в себя метод наименьших квадратов , метод объединения соседей , метод экономии , метод максимального правдоподобия и байесовский вывод .
Биологи иногда используют термин «экономия» для определенного вида алгоритма генерации кладограммы, а иногда как общий термин для всех филогенетических алгоритмов. [15]
Алгоритмы, которые выполняют задачи оптимизации (например, построение кладограмм), могут быть чувствительны к порядку, в котором представлены входные данные (список видов и их характеристики). Ввод данных в разных порядках может привести к тому, что один и тот же алгоритм будет выдавать разные «лучшие» кладограммы. В таких ситуациях пользователь должен вводить данные в разных порядках и сравнивать результаты.
Использование разных алгоритмов на одном наборе данных иногда может приводить к получению разных «лучших» кладограмм, поскольку каждый алгоритм может иметь уникальное определение того, что является «лучшим».
Из-за астрономического числа возможных кладограмм алгоритмы не могут гарантировать, что решение является наилучшим решением в целом. Неоптимальная кладограмма будет выбрана, если программа остановится на локальном минимуме, а не на желаемом глобальном минимуме. [16] Чтобы помочь решить эту проблему, многие алгоритмы кладограмм используют подход имитации отжига, чтобы увеличить вероятность того, что выбранная кладограмма является оптимальной. [17]
Базальное положение — это направление основания (или корня) укорененного филогенетического дерева или кладограммы. Базальная клада — это самая ранняя клада (данного таксономического ранга[a]), ответвляющаяся в пределах более крупной клады.
Тест на разницу в длине несоответствия (ILD) — это измерение того, как сочетание различных наборов данных (например, морфологических и молекулярных, пластидных и ядерных генов) способствует более длинному дереву. Он измеряется путем первого расчета общей длины дерева каждого раздела и их суммирования. Затем производятся репликации путем создания случайно собранных разделов, состоящих из исходных разделов. Длины суммируются. Значение p 0,01 получается для 100 репликаций, если 99 репликаций имеют более длинные объединенные длины деревьев.
Некоторые меры пытаются измерить количество гомоплазии в наборе данных относительно дерева, [18] хотя не всегда ясно, какое именно свойство эти меры стремятся количественно оценить [19]
Индекс согласованности (CI) измеряет согласованность дерева с набором данных — меру минимального количества гомоплазии, подразумеваемого деревом. [20] Он рассчитывается путем подсчета минимального количества изменений в наборе данных и деления его на фактическое количество изменений, необходимых для кладограммы. [20] Индекс согласованности также может быть рассчитан для отдельного символа i , обозначаемого c i .
Помимо отражения количества гомоплазии, метрика также отражает количество таксонов в наборе данных [21], (в меньшей степени) количество символов в наборе данных [22], степень, в которой каждый символ несет филогенетическую информацию [23] , и способ, которым кодируются аддитивные символы, что делает его непригодным для использования по назначению. [24]
c i занимает диапазон от 1 до 1/[ n.taxa /2] в двоичных символах с равномерным распределением состояний; его минимальное значение больше, когда состояния распределены неравномерно. [23] [18] В общем случае для двоичного или недвоичного символа с , c i занимает диапазон от 1 до . [23]
Индекс сохранения (RI) был предложен как улучшение CI "для определенных приложений" [25]. Эта метрика также подразумевает измерение количества гомоплазии, но также измеряет, насколько хорошо синапоморфии объясняют дерево. Он рассчитывается путем взятия (максимального количества изменений на дереве за вычетом количества изменений на дереве) и деления на (максимальное количество изменений на дереве за вычетом минимального количества изменений в наборе данных).
Перемасштабированный индекс согласованности (RC) получается путем умножения CI на RI; по сути, это расширяет диапазон CI таким образом, что его минимальное теоретически достижимое значение перемасштабируется до 0, а его максимальное значение остается на уровне 1. [18] [25] Индекс гомоплазии (HI) просто равен 1 − CI.
Это измеряет количество гомоплазии, наблюдаемое на дереве, относительно максимального количества гомоплазии, которое теоретически может присутствовать – 1 − (наблюдаемый избыток гомоплазии) / (максимальный избыток гомоплазии). [22] Значение 1 указывает на отсутствие гомоплазии; 0 представляет столько гомоплазии, сколько было бы в полностью случайном наборе данных, а отрицательные значения указывают на еще большее количество гомоплазии (и, как правило, встречаются только в надуманных примерах). [22] HER представлен как наилучшая доступная в настоящее время мера гомоплазии. [18] [26]