Код с низкой плотностью проверки на четность

Линейный код исправления ошибок

В теории информации код с низкой плотностью проверок на четность ( LDPC ) — это линейный код исправления ошибок , метод передачи сообщения по зашумленному каналу передачи. ^{[1] [2]} Код LDPC строится с использованием разреженного графа Таннера (подкласс двудольного графа ). ^[3] Коды LDPC являются кодами, приближающимися к емкости , что означает, что существуют практические конструкции, которые позволяют устанавливать порог шума очень близко к теоретическому максимуму ( пределу Шеннона ) для симметричного канала без памяти. Порог шума определяет верхнюю границу для шума канала, до которой вероятность потери информации может быть сделана сколь угодно малой. Используя итеративные методы распространения убеждений , коды LDPC могут быть декодированы за время, линейное по длине их блока.

Коды LDPC также известны как коды Галлагера , в честь Роберта Г. Галлагера , который разработал концепцию LDPC в своей докторской диссертации в Массачусетском технологическом институте в 1960 году. ^{[4] [5]} Однако коды LDPC требуют вычислительно затратного итеративного декодирования, поэтому они оставались неиспользованными в течение десятилетий. В 1993 году недавно изобретенные турбокоды продемонстрировали, что коды с итеративным декодированием могут значительно превзойти другие коды, используемые в то время, но турбокоды были запатентованы и требовали платы за использование. Это вызвало новый интерес к кодам LDPC, которые, как было показано, имели схожую производительность, но были намного старше и не имели патентов. ^[6] Теперь, когда основополагающий патент на турбокоды истек (29 августа 2013 года), ^{[7] [8]} коды LDPC по-прежнему используются из-за их технических достоинств.

Было показано, что коды LDPC обладают идеальными комбинаторными свойствами. В своей диссертации Галлагер показал, что коды LDPC достигают границы Гилберта–Варшамова для линейных кодов над двоичными полями с высокой вероятностью. В 2020 году было показано, что коды LDPC Галлагера достигают емкости декодирования списков , а также достигают границы Гилберта–Варшамова для линейных кодов над общими полями. ^[9]

История

Непрактичные для реализации, когда впервые были разработаны Галлагером в 1963 году, ^[10] коды LDPC были забыты, пока его работа не была заново открыта в 1996 году. ^[11] Турбокоды , другой класс кодов, приближающихся к емкости, открытый в 1993 году, стали предпочтительной схемой кодирования в конце 1990-х годов, используемой для таких приложений, как Deep Space Network и спутниковая связь . Затем коды LDPC получили возобновленный интерес как непатентованная альтернатива с аналогичной производительностью. ^[6] С тех пор достижения в кодах с низкой плотностью проверок на четность показали, что они превзошли турбокоды с точки зрения минимального уровня ошибок и производительности в диапазоне более высоких скоростей кодирования , оставив турбокоды более подходящими только для более низких скоростей кодирования. ^[12]

Приложения

В 2003 году LDPC-код с нерегулярным повторным накоплением (IRA) победил шесть турбокодов и стал кодом с исправлением ошибок в новом стандарте DVB-S2 для цифрового телевидения . ^[13] Комитет по отбору DVB-S2 сделал оценки сложности декодера для предложений турбокода, используя гораздо менее эффективную архитектуру последовательного декодера вместо архитектуры параллельного декодера. Это заставило предложения турбокода использовать размеры кадров порядка половины размера кадров предложений LDPC. ^{[ необходима цитата ]}

В 2008 году LDPC превзошли сверточные турбокоды в качестве системы прямой коррекции ошибок (FEC) для стандарта ITU-T G.hn. ^[14] G.hn выбрал коды LDPC вместо турбокодов из-за их меньшей сложности декодирования (особенно при работе со скоростями передачи данных, близкими к 1,0 Гбит/с) и потому, что предложенные турбокоды показали значительный минимальный уровень ошибок в желаемом диапазоне работы. ^[15]

Коды LDPC также используются для 10GBASE-T Ethernet, который отправляет данные со скоростью 10 гигабит в секунду по витой паре. С 2009 года коды LDPC также являются частью стандарта Wi-Fi 802.11 как необязательная часть 802.11n и 802.11ac в спецификации High Throughput (HT) PHY. ^[16] LDPC является обязательной частью 802.11ax (Wi-Fi 6). ^[17]

Некоторые системы OFDM добавляют дополнительную внешнюю коррекцию ошибок, которая исправляет случайные ошибки («минимальный уровень ошибок»), которые преодолевают внутренний код коррекции LDPC даже при низких коэффициентах битовых ошибок .

Например: Код Рида-Соломона с LDPC-кодированной модуляцией (RS-LCM) использует внешний код Рида-Соломона. ^[18] Стандарты DVB-S2, DVB-T2 и DVB-C2 используют внешний код BCH для устранения остаточных ошибок после декодирования LDPC. ^[19]

5G NR использует полярный код для каналов управления и LDPC для каналов данных. ^{[20] [21]}

Хотя код LDPC имел успех в коммерческих жестких дисках, для полного использования его возможности исправления ошибок в SSD требуется нетрадиционное мелкозернистое зондирование флэш-памяти, что приводит к увеличению задержки чтения памяти. LDPC-in-SSD ^[22] — это эффективный подход к развертыванию LDPC в SSD с очень небольшим увеличением задержки, что превращает LDPC в SSD в реальность. С тех пор LDPC широко применяется в коммерческих SSD как в потребительских, так и в корпоративных классах основными поставщиками хранилищ. Многие SSD TLC (и более поздние) используют коды LDPC. Сначала предпринимается попытка быстрого жесткого декодирования (двоичного стирания), которая может привести к более медленному, но более мощному мягкому декодированию. ^[23]

Эксплуатационное использование

Коды LDPC функционально определяются разреженной матрицей проверки четности . Эта разреженная матрица часто генерируется случайным образом, в зависимости от ограничений разреженности — построение кода LDPC обсуждается позже. Эти коды были впервые разработаны Робертом Галлагером в 1960 году. ^[5]

Ниже представлен фрагмент графа примера кода LDPC с использованием нотации факторного графа Форни . В этом графе n переменных узлов в верхней части графа соединены с ( n − k ) узлами ограничений в нижней части графа.

Это популярный способ графического представления кода LDPC ( n ,  k ). Биты допустимого сообщения, помещенные в T в верхней части графика, удовлетворяют графическим ограничениям. В частности, все линии, соединяющиеся с переменным узлом (ящик со знаком '='), имеют одинаковое значение, а все значения, соединяющиеся с узлом-фактором (ящик со знаком '+'), должны давать в сумме по модулю два ноль (другими словами, их сумма должна быть четным числом; или должно быть четное число нечетных значений).

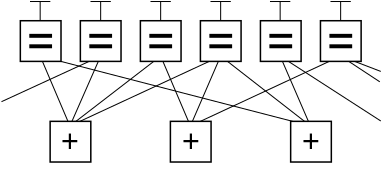
Игнорируя любые линии, выходящие за рамки изображения, существует восемь возможных шестибитных строк, соответствующих допустимым кодовым словам: (т. е. 000000, 011001, 110010, 101011, 111100, 100101, 001110, 010111). Этот фрагмент кода LDPC представляет собой трехбитное сообщение, закодированное как шесть бит. Избыточность используется здесь для увеличения вероятности восстановления после ошибок канала. Это линейный код (6, 3) с n  = 6 и k  = 3.

Опять же, игнорируя линии, выходящие за пределы рисунка, матрица проверки четности, представляющая этот фрагмент графа, имеет вид

${\displaystyle \mathbf {H} ={\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\1&0&0&1&1&0\\\end{pmatrix}}.}$

В этой матрице каждая строка представляет одно из трех ограничений проверки четности, а каждый столбец представляет один из шести битов в полученном кодовом слове.

В этом примере восемь кодовых слов можно получить, приведя матрицу проверки четности H к следующей форме с помощью основных операций над строками в GF(2) : ${\displaystyle {\begin{bmatrix}-P^{T}|I_{n-k}\end{bmatrix}}}$

${\displaystyle \mathbf {H} ={\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\1&0&0&1&1&0\\\end{pmatrix}}_{1}\sim {\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\0&1&1&0&1&0\\\end{pmatrix}}_{2}\sim {\begin{pmatrix}1&1&1&1&0&0\\0&1&1&0&1&0\\0&0&1&1&0&1\\\end{pmatrix}}_{3}\sim {\begin{pmatrix}1&1&1&1&0&0\\0&1&1&0&1&0\\1&1&0&0&0&1\\\end{pmatrix}}_{4}.}$

Шаг 1: Х.

Шаг 2: Строка 1 добавляется к строке 3.

Шаг 3: Строки 2 и 3 меняются местами.

Шаг 4: Строка 1 добавляется к строке 3.

Отсюда матрицу-генератор G можно получить как (отметим, что в частном случае это двоичный код ), или, в частности: ${\displaystyle {\begin{bmatrix}I_{k}|P\end{bmatrix}}}$ ${\displaystyle P=-P}$

${\displaystyle \mathbf {G} ={\begin{pmatrix}1&0&0&1&0&1\\0&1&0&1&1&1\\0&0&1&1&1&0\\\end{pmatrix}}.}$

Наконец, умножая все восемь возможных 3-битных строк на G , получаем все восемь допустимых кодовых слов. Например, кодовое слово для битовой строки '101' получается следующим образом:

${\displaystyle {\begin{pmatrix}1&0&1\\\end{pmatrix}}\odot {\begin{pmatrix}1&0&0&1&0&1\\0&1&0&1&1&1\\0&0&1&1&1&0\\\end{pmatrix}}={\begin{pmatrix}1&0&1&0&1&1\\\end{pmatrix}}}$,

где — символ умножения по модулю 2. ${\displaystyle \odot }$

Для проверки пространство строк G ортогонально H , так что ${\displaystyle G\odot H^{T}=0}$

Битовая строка «101» находится в первых трех битах кодового слова «101011».

Пример кодировщика

LDPC-кодер

Во время кодирования кадра входные биты данных (D) повторяются и распределяются по набору составных кодеров. Составные кодеры обычно являются аккумуляторами, и каждый аккумулятор используется для генерации символа четности. Одна копия исходных данных (S _0,K-1 ) передается с битами четности (P) для составления кодовых символов. Биты S из каждого составного кодера отбрасываются.

Бит четности может использоваться в другом составном коде.

В примере с использованием кода DVB-S2 rate 2/3 размер закодированного блока составляет 64800 символов (N=64800) с 43200 битами данных (K=43200) и 21600 битами четности (M=21600). Каждый составной код (контрольный узел) кодирует 16 бит данных, за исключением первого бита четности, который кодирует 8 бит данных. Первые 4680 бит данных повторяются 13 раз (используются в 13 кодах четности), а оставшиеся биты данных используются в 3 кодах четности (нерегулярный код LDPC).

Для сравнения, классические турбокоды обычно используют два составных кода, сконфигурированных параллельно, каждый из которых кодирует весь входной блок (K) битов данных. Эти составные кодеры представляют собой рекурсивные сверточные коды (RSC) умеренной глубины (8 или 16 состояний), которые разделены перемежателем кодов, который перемежает одну копию кадра.

Код LDPC, напротив, использует много низкоглубинных составных кодов (аккумуляторов) параллельно, каждый из которых кодирует только небольшую часть входного кадра. Многочисленные составные коды можно рассматривать как много низкоглубинных (2 состояния) « сверточных кодов », которые связаны посредством операций повтора и распределения. Операции повтора и распределения выполняют функцию перемежителя в турбокоде.

Возможность более точного управления соединениями различных составных кодов и уровнем избыточности для каждого входного бита обеспечивает большую гибкость в разработке кодов LDPC, что может привести к лучшей производительности, чем турбокоды в некоторых случаях. Турбокоды, по-видимому, все еще работают лучше, чем LDPC на низких скоростях кодирования, или, по крайней мере, разработка хорошо работающих низкоскоростных кодов проще для турбокодов.

На практике аппаратное обеспечение, формирующее аккумуляторы, повторно используется в процессе кодирования. То есть, как только первый набор битов четности сгенерирован и сохранен, то же самое аппаратное обеспечение аккумулятора используется для генерации следующего набора битов четности.

Расшифровка

Как и в случае с другими кодами, декодирование максимального правдоподобия кода LDPC на двоичном симметричном канале является NP-полной задачей, ^[24] показанной путем сокращения из 3-мерного сопоставления . Поэтому, предполагая, что P != NP , что широко распространено, то выполнение оптимального декодирования для произвольного кода любого полезного размера нецелесообразно.

Однако неоптимальные методы, основанные на итеративном декодировании распространения убеждения , дают превосходные результаты и могут быть реализованы на практике. Неоптимальные методы декодирования рассматривают каждую проверку четности, которая составляет LDPC, как независимый одиночный код проверки четности (SPC). Каждый код SPC декодируется отдельно с использованием методов soft-in-soft-out (SISO), таких как SOVA , BCJR , MAP и других их производных. Информация о мягком решении от каждого декодирования SISO перепроверяется и обновляется с другими избыточными декодированиями SPC того же информационного бита. Затем каждый код SPC снова декодируется с использованием обновленной информации о мягком решении. Этот процесс повторяется до тех пор, пока не будет получено допустимое кодовое слово или декодирование не будет исчерпано. Этот тип декодирования часто называют декодированием суммы-произведения.

Декодирование кодов SPC часто называют обработкой «проверочного узла», а перекрестную проверку переменных часто называют обработкой «переменного узла».

В практической реализации декодера LDPC наборы кодов SPC декодируются параллельно для увеличения пропускной способности.

Напротив, распространение убеждений по двоичному каналу стирания особенно просто, когда оно состоит из итеративного удовлетворения ограничений.

Например, предположим, что допустимое кодовое слово 101011 из примера выше передается по двоичному каналу стирания и принимается со стертыми первым и четвертым битами, что дает ?01?11. Поскольку переданное сообщение должно удовлетворять ограничениям кода, сообщение можно представить, записав полученное сообщение в верхней части факторного графика.

В этом примере первый бит пока не может быть восстановлен, поскольку все ограничения, связанные с ним, имеют более одного неизвестного бита. Чтобы продолжить декодирование сообщения, необходимо идентифицировать ограничения, связанные только с одним из стертых битов. В этом примере достаточно только второго ограничения. При рассмотрении второго ограничения четвертый бит должен был быть равен нулю, поскольку только ноль в этой позиции будет удовлетворять ограничению.

Затем эта процедура повторяется. Новое значение для четвертого бита теперь может использоваться в сочетании с первым ограничением для восстановления первого бита, как показано ниже. Это означает, что первый бит должен быть единицей, чтобы удовлетворить самому левому ограничению.

Таким образом, сообщение может быть декодировано итеративно. Для других моделей каналов сообщения, передаваемые между узлами переменных и узлами проверки, являются действительными числами , которые выражают вероятности и правдоподобия веры.

Этот результат можно проверить, умножив исправленное кодовое слово r на матрицу проверки четности H :

${\displaystyle \mathbf {z} =\mathbf {H\odot r} ={\begin{pmatrix}1&1&1&1&0&0\\0&0&1&1&0&1\\1&0&0&1&1&0\\\end{pmatrix}}\odot {\begin{pmatrix}1\\0\\1\\0\\1\\1\\\end{pmatrix}}={\begin{pmatrix}0\\0\\0\\\end{pmatrix}}.}$

Поскольку результатом z ( синдромом ) этой операции является вектор три × один ноль, результирующее кодовое слово r успешно проверяется.

После завершения декодирования исходные биты сообщения «101» можно извлечь, посмотрев на первые 3 бита кодового слова.

Хотя этот пример стирания является иллюстративным, он не демонстрирует использование декодирования с мягким решением или передачи сообщений с мягким решением, которые используются практически во всех коммерческих декодерах LDPC.

Обновление информации об узле

В последние годы ^{[ когда? ]} также было проведено много работы по изучению эффектов альтернативных графиков для обновления узлов переменной и узла ограничения. Первоначальный метод, который использовался для декодирования кодов LDPC, был известен как затопление . Этот тип обновления требовал, чтобы перед обновлением узла переменной все узлы ограничений должны были быть обновлены и наоборот. В более поздней работе Вила Касадо и др. [ ^25] были изучены альтернативные методы обновления, в которых узлы переменной обновляются с использованием новейшей доступной информации о узле проверки. ^{[ требуется цитата ]}

Интуиция, лежащая в основе этих алгоритмов, заключается в том, что переменные узлы, значения которых изменяются больше всего, — это те, которые необходимо обновить в первую очередь. Высоконадежные узлы, величина отношения логарифмического правдоподобия (LLR) которых велика и не меняется существенно от одного обновления к другому, не требуют обновлений с той же частотой, что и другие узлы, знак и величина которых колеблются в более широких пределах. ^{[ необходима цитата ]} Эти алгоритмы планирования показывают большую скорость сходимости и более низкие уровни ошибок, чем те, которые используют лавинную рассылку. Эти более низкие уровни ошибок достигаются благодаря способности алгоритма информированного динамического планирования (IDS) ^[25] преодолевать захваты наборов близких кодовых слов. ^[26]

При использовании алгоритмов планирования без затопления используется альтернативное определение итерации. Для кода LDPC ( n ,  k ) со скоростью k / n полная итерация происходит, когда обновляются n переменных и n  −  k узлов ограничений, независимо от порядка, в котором они обновлялись. ^{[ необходима цитата ]}

Построение кода

Для больших размеров блоков коды LDPC обычно строятся путем предварительного изучения поведения декодеров. Поскольку размер блока стремится к бесконечности, можно показать, что декодеры LDPC имеют порог шума, ниже которого декодирование надежно достигается, и выше которого декодирование не достигается, ^[27] в разговорной речи называемый эффектом обрыва . Этот порог можно оптимизировать, найдя наилучшую пропорцию дуг из контрольных узлов и дуг из переменных узлов. Приблизительный графический подход к визуализации этого порога — это диаграмма EXIT . ^{[ необходима цитата ]}

Построение конкретного кода LDPC после этой оптимизации можно разделить на два основных типа методов: ^{[ необходимая ссылка ]}

• Псевдослучайные подходы
• Комбинаторные подходы

Построение с помощью псевдослучайного подхода основывается на теоретических результатах, согласно которым для большого размера блока случайное построение обеспечивает хорошую производительность декодирования. ^[11] В общем случае псевдослучайные коды имеют сложные кодировщики, но псевдослучайные коды с лучшими декодерами могут иметь простые кодировщики. ^[28] Часто применяются различные ограничения, чтобы гарантировать, что желаемые свойства, ожидаемые при теоретическом пределе бесконечного размера блока, реализуются при конечном размере блока. ^{[ необходима цитата ]}

Комбинаторные подходы могут быть использованы для оптимизации свойств кодов LDPC с малым размером блока или для создания кодов с простыми кодерами. ^{[ необходима цитата ]}

Некоторые коды LDPC основаны на кодах Рида-Соломона , например, код RS-LDPC, используемый в стандарте 10 Gigabit Ethernet . ^[29] По сравнению со случайно сгенерированными кодами LDPC, структурированные коды LDPC, например, код LDPC, используемый в стандарте DVB-S2 , могут иметь более простое и, следовательно, менее затратное оборудование, в частности, коды, построенные таким образом, что матрица H является циркулянтной матрицей . ^[30]

Еще один способ построения кодов LDPC — это использование конечных геометрий . Этот метод был предложен Y. Kou и др. в 2001 году. ^[31]

По сравнению с турбокодами

Коды LDPC можно сравнить с другими мощными схемами кодирования, например, турбокодами . ^[32] С одной стороны, на производительность BER турбокодов влияют ограничения низких кодов. ^[33] Коды LDPC не имеют ограничений минимального расстояния, ^[34] что косвенно означает, что коды LDPC могут быть более эффективными на относительно больших скоростях кодирования (например, 3/4, 5/6, 7/8), чем турбокоды. Однако коды LDPC не являются полной заменой: турбокоды являются лучшим решением на более низких скоростях кодирования (например, 1/6, 1/3, 1/2). ^{[35] [36]}

Смотрите также

Люди

• Ричард Хэмминг
• Клод Шеннон
• Дэвид Дж. К. Маккей
• Ирвинг С. Рид
• Майкл Луби

Теория

• Теория графов
• Код Хэмминга
• Код разреженного графа
• Расширительный код

Приложения

• G.hn/G.9960 (стандарт ITU-T для сетей по линиям электропередач, телефонным линиям и коаксиальному кабелю)
• 802.3an или 10GBASE-T (10 Гбит/с Ethernet по витой паре)
• CMMB (Китайское мультимедийное мобильное вещание)
• DVB-S2 / DVB-T2 / DVB-C2 (цифровое видеовещание, 2-е поколение)
• DMB-T/H (цифровое видеовещание) ^[37]
• WiMAX (стандарт IEEE 802.16e для микроволновой связи)
• IEEE 802.11n-2009 ( стандарт Wi-Fi )
• DOCSIS 3.1
• ATSC 3.0 (цифровое наземное вещание следующего поколения в Северной Америке)
• 3GPP (канал передачи данных 5G-NR)

Другие коды приближения к емкости

• Фонтанные коды
• LT-коды
• Онлайн-коды
• Коды Raptor
• Повторно-накопительные коды (класс простых турбокодов)
• Последовательные каскадные сверточные коды
• Коды Торнадо (коды LDPC, предназначенные для декодирования стирания )
• Турбо-коды

Коды достижения производительности

На данный момент существует только одна возможность достижения кода путем проектирования и доказательства.

• Полярные коды

Ссылки

1. MacKay, David J. (2003). Теория информации, алгоритмы вывода и обучения. Cambridge University Press. ISBN 0-521-64298-1.
2. Мун, Тодд К. (2005). Кодирование с исправлением ошибок, математические методы и алгоритмы . Wiley. ISBN 0-471-64800-0.(Включает код)
3. Амин Шокроллахи, Коды LDPC: Введение (PDF) , заархивировано из оригинала (PDF) 17 мая 2017 г.
4. Hardesty, L. (21 января 2010 г.). "Объяснение: коды Галлагера". MIT News . Получено 7 августа 2013 г. .
5. Gallager, RG (январь 1962). "Коды с низкой плотностью проверки четности". IRE Trans. Inf. Theory . 8 (1): 21–28. doi :10.1109/TIT.1962.1057683. hdl :1721.1/11804/32786367-MIT. S2CID  260490814.
6. Эрико Гиццо (1 марта 2004 г.). "CLOSING IN ON THE PERFECT CODE". IEEE Spectrum . Архивировано из оригинала 2 сентября 2021 г.«Еще одним преимуществом, возможно, самым большим из всех, является то, что срок действия патентов LDPC истек, поэтому компании могут использовать их, не платя за права интеллектуальной собственности».
7. США 5446747 
8. Маккензи, Д. (9 июля 2005 г.). «Скорость связи приближается к предельной скорости». New Scientist .
9. Mosheiff, J.; Resch, N.; Ron-Zewi, N.; Silas, S.; Wootters, M. (2020). «Коды с низкой плотностью проверки на четность достигают емкости декодирования списков». SIAM Journal on Computing (FOCS 2020): 38–73. arXiv : 1909.06430 . doi :10.1137/20M1365934. S2CID  244549036.
10. Галлагер, Роберт Г. (1963). Коды с низкой плотностью проверки четности (PDF) . MIT Press . Получено 7 августа 2013 г. .
11. Дэвид Дж. К. Маккей и Рэдфорд М. Нил, «Производительность кодов с низкой плотностью проверок на четность, близкая к пределу Шеннона», Electronics Letters, июль 1996 г.
12. Декодирование телеметрических данных, Справочник по проектированию
13. Презентация Hughes Systems, архив 2006-10-08 на Wayback Machine
14. HomePNA Блог: G.hn, PHY на все времена
15. Статья журнала IEEE Communications Magazine о G.hn. Архивировано 13 декабря 2009 г. на Wayback Machine.
16. Стандарт IEEE, раздел 20.3.11.6 «802.11n-2009», IEEE, 29 октября 2009 г., дата обращения 21 марта 2011 г.
17. "IEEE SA - IEEE 802.11ax-2021". Ассоциация стандартов IEEE . Получено 22 мая 2022 г.
18. Чи-Юань Ян, Монг-Кай Ку. http://123seminarsonly.com/Seminar-Reports/029/26540350-Ldpc-Coded-Ofdm-Modulation.pdf «Модуляция OFDM с кодированием LDPC для передачи с высокой спектральной эффективностью»
19. Ник Уэллс. «DVB-T2 в отношении к семейству стандартов DVB-x2» Архивировано 26.05.2013 на Wayback Machine
20. "5G Channel Coding" (PDF) . Архивировано из оригинала (PDF) 6 декабря 2018 г. . Получено 6 января 2019 г. .
21. Maunder, Robert (сентябрь 2016 г.). "Видение кодирования каналов 5G" (PDF) . Архивировано из оригинала (PDF) 6 декабря 2018 г. . Получено 6 января 2019 г. .
22. Кай Чжао; Вэньчжэ Чжао; Хунбинь Сан; Тун Чжан; Сяодун Чжан; Наньнин Чжэн (2013). LDPC-in-SSD: обеспечение эффективной работы расширенных кодов исправления ошибок в твердотельных накопителях (PDF) . FAST' 13. стр. 243–256.
23. «Мягкое декодирование в контроллерах SSD на базе LDPC». EE Times . 2015.
24. Роберт Мак-Элис, Э. Р. Берлекамп и Х. Ван Тилборг (1978). «О внутренней неразрешимости некоторых проблем кодирования». IEEE Trans. Inf. Theory . IEEE: 384–386. doi :10.1109/TIT.1978.1055873.
25. Casado, AIV; Griot, M.; Wesel, RD (2007). Информированное динамическое планирование для декодирования кодов LDPC с распространением убеждения . Международная конференция IEEE по коммуникациям, Глазго, Великобритания, 2007 г., стр. 932–7. arXiv : cs/0702111 . doi :10.1109/ICC.2007.158.
26. Ричардсон, Т. (октябрь 2003 г.). "Уровни ошибок кодов LDPC" (PDF) . Труды Ежегодной конференции Аллертона по управлению связью и вычислениям . 41 (3): 1426–35. ISSN  0732-6181.
27. Ричардсон, Т. Дж.; Шокроллахи, МА; Урбанке, Р. Л. (февраль 2001 г.). «Разработка нерегулярных кодов с низкой плотностью проверок на четность, приближающихся к емкости». Труды IEEE по теории информации . 47 (2): 619–637. doi :10.1109/18.910578.
28. Ричардсон, Т. Дж.; Урбанке, Р. Л. (февраль 2001 г.). «Эффективное кодирование кодов с низкой плотностью проверки четности». Труды IEEE по теории информации . 47 (2): 638–656. doi :10.1109/18.910579.
29. Ахмад Дарабиха, Энтони Чан Карусон, Фрэнк Р. Кшишанг. «Методы снижения мощности для декодеров LDPC»
30. Чжан, З.; Анантхарам, В.; Уэйнрайт, М. Дж.; Николич, Б. (апрель 2010 г.). «Эффективная конструкция декодера Ethernet LDPC 10GBASE-T с низким уровнем ошибок» (PDF) . IEEE Journal of Solid-State Circuits . 45 (4): 843–855. Bibcode : 2010IJSSC..45..843Z. doi : 10.1109/JSSC.2010.2042255. S2CID  10431486.
31. Kou, Y.; Lin, S.; Fossorier, MPC (ноябрь 2001 г.). «Коды с низкой плотностью проверки на четность, основанные на конечных геометриях: повторное открытие и новые результаты». IEEE Transactions on Information Theory . 47 (7): 2711–36. CiteSeerX 10.1.1.100.3023 . doi :10.1109/18.959255. 
32. Тахир, Б.; Шварц, С.; Рапп, М. (2017). Сравнение BER между сверточным, турбо, LDPC и полярным кодами . 2017 24-я Международная конференция по телекоммуникациям (ИКТ), Лимасол, Кипр. стр. 1–7. doi :10.1109/ICT.2017.7998249.
33. Мун Тодд, К. (2005). Кодирование с исправлением ошибок: математические методы и алгоритмы . Wiley. стр. 614. ISBN 0-471-64800-0.
34. Мун Тодд 2005, стр. 653
35. Эндрюс, Кеннет С. и др. «Разработка турбо- и LDPC-кодов для приложений дальнего космоса». Труды IEEE 95.11 (2007): 2142-2156.
36. Хассан, АЕС, Дессоуки, М., Абу Элазм, А. и Шокайр, М., 2012. Оценка сложности в зависимости от производительности для турбокода и LDPC при различных скоростях кодирования. Proc. SPACOMM, стр. 93-98.
37. "IEEE Spectrum: Имеет ли Китай лучший стандарт цифрового телевидения на планете?". IEEE . Архивировано из оригинала 12 декабря 2009 г.

Внешние ссылки

• Знакомство с кодами с низкой плотностью проверок на четность (Сара Дж. Джонсон, 2010)
• Коды LDPC – краткое руководство (Бернхард Лейнер, 2005 г.)
• Коды LDPC (TU Wien) Архивировано 28 февраля 2019 г. на Wayback Machine
• MacKay, David JC (25 сентября 2003 г.). "47. Коды с низкой плотностью проверки на четность". Теория информации, вывод и алгоритмы обучения. Cambridge University Press. стр. 557–573. ISBN 9780521642989.
• Гурусвами, Венкатесан (2006). «Итеративное декодирование кодов с низкой плотностью проверки четности». arXiv : cs/0610022 .
• Коды LDPC: Введение (Амин Шокроллахи, 2003)
• Декодирование кодов LDPC с помощью распространения убеждений (Амир Беннатан, Принстонский университет)
• Турбо- и LDPC-коды: реализация, моделирование и стандартизация (Университет Западной Вирджинии)
• Теория информации и кодирование (Марко Хеннхёфер, 2011, Технический университет Ильменау) — обсуждает коды LDPC на страницах 74–78.
• Коды LDPC и результаты производительности
• Канал DVB-S.2, включая кодирование LDPC (MatLab)
• Исходный код для кодирования, декодирования и моделирования кодов LDPC доступен в различных местах:
  • Двоичные коды LDPC на языке C
  • Двоичные коды LDPC для Python (основной алгоритм на языке C)
  • Кодер LDPC и декодер LDPC в MATLAB
  • Fast Forward Error Correction Toolbox (AFF3CT) на языке C++11 для быстрого моделирования LDPC