Напряжение цилиндра

Распределение напряжений с вращательной симметрией

В механике цилиндрическое напряжение представляет собой распределение напряжений с вращательной симметрией, то есть, которое остается неизменным, если напряженный объект вращается вокруг некоторой фиксированной оси.

Модели напряжений цилиндра включают в себя:

• окружное напряжение , или кольцевое напряжение , нормальное напряжение в тангенциальном ( азимутальном ) направлении.
• осевое напряжение , нормальное напряжение, параллельное оси цилиндрической симметрии.
• радиальное напряжение , нормальное напряжение в направлениях, копланарных, но перпендикулярных оси симметрии.

Эти три главных напряжения — кольцевое, продольное и радиальное — можно рассчитать аналитически, используя взаимно перпендикулярную трехосную систему напряжений. ^[1]

Классический пример (и тезка) кольцевого напряжения — это натяжение, приложенное к железным полосам или обручам деревянной бочки . В прямой закрытой трубе любая сила, приложенная к цилиндрической стенке трубы разницей давлений, в конечном итоге приведет к кольцевым напряжениям. Аналогично, если эта труба имеет плоские торцевые крышки, любая сила, приложенная к ним статическим давлением, вызовет перпендикулярное осевое напряжение на той же стенке трубы. Тонкие секции часто имеют пренебрежимо малое радиальное напряжение , но точные модели более толстостенных цилиндрических оболочек требуют учета таких напряжений.

В толстостенных сосудах высокого давления могут использоваться методы строительства, позволяющие получить благоприятные начальные схемы напряжений. Эти сжимающие напряжения на внутренней поверхности снижают общее окружное напряжение в цилиндрах высокого давления. Цилиндрические сосуды такого типа обычно изготавливаются из концентрических цилиндров, усаженных друг на друга (или расширенных друг в друга), т. е. сборных цилиндров с горячей посадкой, но также могут быть выполнены для отдельных цилиндров посредством автофреттажа толстых цилиндров. ^[2]

Определения

Обруч стресса

Компоненты кольцевого напряжения

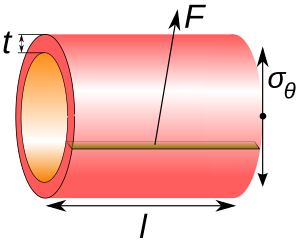
Кольцевое напряжение — это сила, действующая по окружности (перпендикулярно оси и радиусу объекта) в обоих направлениях на каждую частицу в стенке цилиндра. Ее можно описать как:

${\displaystyle \sigma _{\theta }={\dfrac {F}{tl}}\ }$

где:

• F — сила , действующая по окружности на область стенки цилиндра, имеющую следующие две длины сторон:
• t — радиальная толщина цилиндра
• l — осевая длина цилиндра.

Альтернативой кольцевому напряжению при описании окружного напряжения является напряжение стенки или растяжение стенки ( T ), которое обычно определяется как общая окружная сила, действующая по всей радиальной толщине: ^[3]

${\displaystyle T={\dfrac {F}{l}}\ }$

Цилиндрические координаты

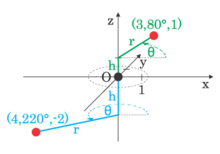
Наряду с осевым и радиальным напряжениями окружное напряжение является компонентом тензора напряжений в цилиндрических координатах .

Обычно бывает полезно разложить любую силу, приложенную к объекту с вращательной симметрией , на компоненты, параллельные цилиндрическим координатам r , z и θ . Эти компоненты силы вызывают соответствующие напряжения: радиальное напряжение, осевое напряжение и кольцевое напряжение соответственно.

Отношение к внутреннему давлению

Тонкостенное предположение

Для того чтобы предположение о тонкостенности было верным, толщина стенки сосуда должна составлять не более одной десятой (часто упоминается как Диаметр / t > 20) его радиуса. ^[4] Это позволяет рассматривать стенку как поверхность и впоследствии использовать уравнение Юнга-Лапласа для оценки окружного напряжения, создаваемого внутренним давлением на тонкостенном цилиндрическом сосуде высокого давления:

${\displaystyle \sigma _{\theta }={\dfrac {Pr}{t}}\ }$ (для цилиндра)

${\displaystyle \sigma _{\theta }={\dfrac {Pr}{2t}}\ }$ (для сферы)

где

• P — внутреннее давление
• t — толщина стенки
• r — средний радиус цилиндра
• ${\displaystyle \sigma _{\theta }\!}$это обручальное напряжение.

Уравнение кольцевого напряжения для тонких оболочек также приблизительно справедливо для сферических сосудов, включая растительные клетки и бактерии, в которых внутреннее тургорное давление может достигать нескольких атмосфер. В практических инженерных приложениях для цилиндров (труб и трубок) кольцевое напряжение часто перестраивается для давления и называется формулой Барлоу .

Единицами измерения P в системе дюйм-фунт-секунда (IPS) являются фунты-силы на квадратный дюйм (psi). Единицами измерения t и d являются дюймы (in). Единицами измерения P в системе СИ являются паскали (Па), а t и d =2 r измеряются в метрах (м).

Когда сосуд имеет закрытые концы, внутреннее давление действует на них, создавая силу вдоль оси цилиндра. Это известно как осевое напряжение и обычно меньше окружного напряжения.

${\displaystyle \sigma _{z}={\dfrac {F}{A}}={\dfrac {Pd^{2}}{(d+2t)^{2}-d^{2}}}\ }$

Хотя это может быть приближено к

${\displaystyle \sigma _{z}={\dfrac {Pr}{2t}}\ }$

Существует также радиальное напряжение , которое развивается перпендикулярно поверхности и может быть оценено в тонкостенных цилиндрах как: ${\displaystyle \sigma _{r}\ }$

${\displaystyle \sigma _{r}={-P}\ }$

В предположении тонкостенности отношение велико, поэтому в большинстве случаев этот компонент считается незначительным по сравнению с окружными и осевыми напряжениями. ^[5] ${\displaystyle {\dfrac {r}{t}}\ }$

Толстостенные сосуды

Если изучаемый цилиндр имеет отношение менее 10 (часто упоминается как ), уравнения для тонкостенного цилиндра больше не выполняются, поскольку напряжения значительно различаются между внутренней и внешней поверхностями, а напряжением сдвига через поперечное сечение больше нельзя пренебрегать. ${\displaystyle {\text{radius}}/{\text{thickness}}}$ ${\displaystyle {\text{diameter}}/{\text{thickness}}<20}$

Эти напряжения и деформации можно рассчитать с помощью уравнений Ламе ^[6] , набора уравнений, разработанных французским математиком Габриэлем Ламе .

${\displaystyle \sigma _{r}=A-{\dfrac {B}{r^{2}}}\ }$

${\displaystyle \sigma _{\theta }=A+{\dfrac {B}{r^{2}}}\ }$

где:

${\displaystyle A}$и являются константами интегрирования, которые можно найти из граничных условий, ${\displaystyle B}$

${\displaystyle r}$— радиус в интересующей точке (например, у внутренней или внешней стены).

Для цилиндра с граничными условиями:

${\displaystyle p(r=a)=P_{a}}$(т.е. внутреннее давление на внутренней поверхности), ${\displaystyle P_{a}}$

${\displaystyle p(r=b)=P_{b}}$(т.е. внешнее давление на наружную поверхность), ${\displaystyle P_{b}}$

получены следующие константы:

${\displaystyle A={\dfrac {P_{a}a^{2}-P_{b}b^{2}}{b^{2}-a^{2}}}\ }$,

${\displaystyle B={\dfrac {a^{2}b^{2}(P_{a}-P_{b})}{b^{2}-a^{2}}}\ }$.

Используя эти константы, получаем следующее уравнение для кольцевого напряжения:

${\displaystyle \sigma _{\theta }={\dfrac {P_{a}a^{2}-P_{b}b^{2}}{b^{2}-a^{2}}}+{\dfrac {a^{2}b^{2}(P_{a}-P_{b})}{(b^{2}-a^{2})r^{2}}}\ }$

Для сплошного цилиндра: тогда и сплошной цилиндр не может иметь внутреннего давления, поэтому . ${\displaystyle R_{i}=0}$ ${\displaystyle B=0}$ ${\displaystyle A=P_{o}}$

Поскольку для толстостенных цилиндров это отношение меньше 10, радиальное напряжение по отношению к другим напряжениям становится непренебрежимо малым (т.е. P уже не намного, намного меньше Pr/t и Pr/2t), и поэтому толщина стенки становится основным фактором при проектировании (Харви, 1974, стр. 57). ${\displaystyle {\dfrac {r}{t}}\ }$

В теории сосудов высокого давления любой заданный элемент стенки оценивается в трехосной системе напряжений, где три главных напряжения — кольцевое, продольное и радиальное. Поэтому, по определению, не существует касательных напряжений на поперечной, тангенциальной или радиальной плоскостях. ^[1]

В толстостенных цилиндрах максимальное касательное напряжение в любой точке определяется половиной алгебраической разности между максимальным и минимальным напряжениями, которая, следовательно, равна половине разности между кольцевым и радиальным напряжениями. Касательное напряжение достигает максимума на внутренней поверхности, что имеет значение, поскольку служит критерием разрушения, поскольку хорошо коррелирует с фактическими испытаниями на разрыв толстых цилиндров (Harvey, 1974, стр. 57).

Практические эффекты

Инженерное дело

Разрушение регулируется кольцевым напряжением при отсутствии других внешних нагрузок, поскольку это наибольшее главное напряжение. Обратите внимание, что кольцо испытывает наибольшее напряжение внутри (снаружи и внутри испытывают одинаковую общую деформацию, которая распределена по разным окружностям); следовательно, трещины в трубах теоретически должны начинаться изнутри трубы . Вот почему осмотры труб после землетрясений обычно включают отправку камеры внутрь трубы для осмотра на наличие трещин. Текучесть регулируется эквивалентным напряжением, которое включает кольцевое напряжение и продольное или радиальное напряжение при его отсутствии.

Лекарство

При патологии стенок сосудов или желудочно -кишечного тракта напряжение стенки представляет собой мышечное напряжение на стенке сосуда. В результате закона Лапласа , если аневризма образуется в стенке кровеносного сосуда, радиус сосуда увеличивается. Это означает, что внутренняя сила на сосуде уменьшается, и поэтому аневризма будет продолжать расширяться, пока не разорвется. Подобная логика применима к образованию дивертикулов в кишечнике . ^[7]

Развитие теории

Чугунная опора железнодорожного моста Чепстоу , 1852 г. Шарнирно-сочлененные обручи из кованого железа (более прочные на растяжение, чем чугунные) выдерживают кольцевые напряжения. ^[8]

Первый теоретический анализ напряжения в цилиндрах был разработан инженером середины 19 века Уильямом Фейрберном , которому помогал его математический аналитик Итон Ходжкинсон . Их первым интересом было изучение конструкции и отказов паровых котлов . ^[9] Фейрберн понял, что кольцевое напряжение было вдвое больше продольного напряжения, что является важным фактором при сборке корпусов котлов из прокатанных листов, соединенных клепкой . Позднее работа была применена в строительстве мостов и изобретении коробчатой ​​балки . В железнодорожном мосту Чепстоу чугунные столбы усилены внешними полосами кованого железа . Вертикальная продольная сила является сжимающей силой, которой чугун хорошо способен противостоять. Окружное напряжение является растягивающим, и поэтому добавляется кованое железо, материал с лучшей прочностью на растяжение, чем чугун.

Смотрите также

• Может быть вызвано напряжением цилиндра:
  • Бостонская катастрофа с патокой
  • Взрыв котла
  • Взрыв расширяющегося пара при кипении жидкости
• Смежные инженерные темы:
  • Концентрация напряжения
  • Гидростатическое испытание
  • Выпучивание
  • Кровяное давление#Отношение_к_напряжению_стены
  • Трубопровод#Анализ_напряжения
• Конструкции, сильно подверженные этому стрессу:
  • Сосуд под давлением
    • Ракетный двигатель
  • Маховик
  • Купол Флорентийского собора

Ссылки

1. "Advanced Structural Analysis" (PDF) . Университет Суонси. 2020. стр. 8. Архивировано из оригинала (PDF) 19 августа 2019 г.
2. Харви, Джон Ф. (1974). «Теория и проектирование современных сосудов высокого давления». Ван Ностранд Рейнхольд. С. 60–61.
3. Напряжение в стенках артерий Автор: Р. Нав. Кафедра физики и астрономии, Университет штата Джорджия. Получено в июне 2011 г.
4. «Сосуд под давлением, тонкостенное кольцевое и продольное напряжение. Уравнение и калькулятор — Engineers Edge».
5. "Сосуды высокого давления" (PDF) . web.mit.edu . Получено 2020-06-12 .
6. "Механика материалов - Часть 35 (Толстый цилиндр - уравнение Ламе)". youtube.com . Получено 23 октября 2022 г. .
7. Э. Гольян, Патология, 2-е изд. Mosby Elsevier, Rapid Review Series.
8. Джонс, Стивен К. (2009). Брунель в Южном Уэльсе . Том II: Коммуникации и уголь. Страуд: The History Press. стр. 247. ISBN 9780752449128.
9. Фэрберн, Уильям (1851). «Строительство котлов». Две лекции: «Строительство котлов» и «О взрывах котлов и средствах их предотвращения». стр. 6.

• Тонкостенные сосуды высокого давления. 19 июня 2008 г. {{cite book}}: |work=проигнорировано ( помощь )