В термодинамике жидкости конвекция Рэлея-Бенара — это тип естественной конвекции , происходящей в плоском горизонтальном слое жидкости , нагретой снизу, в котором жидкость образует регулярный рисунок конвективных ячеек, известных как ячейки Бенара . Такие системы были впервые исследованы Жозефом Валентином Буссинеском [1] и Антоном Обербеком [2] в 19 веке. Это явление может также проявляться, когда вещество, более плотное, чем электролит, потребляется снизу и генерируется наверху. [3] Конвекция Бенара-Рэлея является одним из наиболее часто изучаемых явлений конвекции из-за ее аналитической и экспериментальной доступности. [4] Модели конвекции являются наиболее тщательно изученным примером самоорганизующихся нелинейных систем . [4] [5] Известны зависящие от времени самоподобные аналитические решения для полей скорости, а также для распределения температуры. [6] [7]
Плавучесть , а следовательно, и гравитация , ответственны за появление конвективных ячеек. Начальное движение — это подъем менее плотной жидкости из более теплого нижнего слоя. [8] Этот подъем спонтанно организуется в регулярную структуру ячеек.

Характеристики конвекции Бенара можно получить с помощью простого эксперимента, впервые проведенного французским физиком Анри Бенаром в 1900 году.
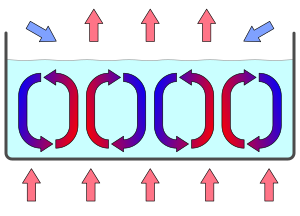
Экспериментальная установка использует слой жидкости, например, воды, между двумя параллельными плоскостями. Высота слоя мала по сравнению с горизонтальным измерением. Сначала температура нижней плоскости такая же, как и верхней плоскости. Затем жидкость будет стремиться к равновесию , где ее температура такая же, как и ее окружение. (Оказавшись там, жидкость становится совершенно однородной: для наблюдателя она будет казаться одинаковой из любого положения. Это равновесие также асимптотически устойчиво : после локального временного возмущения внешней температуры она вернется в свое однородное состояние в соответствии со вторым законом термодинамики ).
Затем температура нижней плоскости немного повышается, что приводит к потоку тепловой энергии, проходящему через жидкость. Система начнет иметь структуру теплопроводности : температура, а вместе с ней и плотность и давление, будут линейно изменяться между нижней и верхней плоскостью. Установится равномерный линейный градиент температуры. (Эта система может быть смоделирована статистической механикой ).
После установления проводимости микроскопическое случайное движение спонтанно становится упорядоченным на макроскопическом уровне, образуя ячейки конвекции Бенара с характерной длиной корреляции.

Вращение ячеек стабильно и будет чередоваться с вращения по часовой стрелке на вращение против часовой стрелки по горизонтали; это пример спонтанного нарушения симметрии . Ячейки Бенара метастабильны . Это означает, что небольшое возмущение не сможет изменить вращение ячеек, но более сильное может повлиять на вращение; они демонстрируют форму гистерезиса .
Более того, детерминированный закон на микроскопическом уровне производит недетерминированное расположение ячеек: если эксперимент повторяется, то определенная позиция в эксперименте будет в ячейке по часовой стрелке в некоторых случаях и против часовой стрелки в других. Микроскопических возмущений начальных условий достаточно, чтобы произвести недетерминированный макроскопический эффект. То есть, в принципе, нет способа вычислить макроскопический эффект микроскопического возмущения. Эта неспособность предсказать условия на дальнем расстоянии и чувствительность к начальным условиям являются характеристиками хаотических или сложных систем (т. е. эффект бабочки ).
Если бы температура нижней плоскости увеличилась еще больше, структура стала бы более сложной в пространстве и времени; турбулентный поток стал бы хаотичным .
Конвективные ячейки Бенара имеют тенденцию приближаться к правильным шестиугольным призмам, особенно при отсутствии турбулентности, [10] [11] [12], хотя определенные экспериментальные условия могут привести к образованию правильных квадратных призм [13] или спиралей. [14]
Конвективные ячейки Бенара не являются уникальными и обычно появляются только в конвекции, вызванной поверхностным натяжением. В общем случае решения анализа Рэлея и Пирсона [15] (линейная теория), предполагающие бесконечный горизонтальный слой, приводят к вырождению, что означает, что система может получить множество шаблонов. Предполагая равномерную температуру на верхней и нижней пластинах, когда используется реалистичная система (слой с горизонтальными границами), форма границ будет определять шаблон. Чаще всего конвекция будет выглядеть как рулоны или их суперпозиция.
Поскольку между верхней и нижней пластиной существует градиент плотности, гравитация пытается перетянуть более холодную, более плотную жидкость сверху вниз. Эта гравитационная сила противостоит силе вязкого затухания в жидкости. Баланс этих двух сил выражается безразмерным параметром, называемым числом Рэлея . Число Рэлея определяется как:
где
С ростом числа Рэлея гравитационные силы становятся более доминирующими. При критическом числе Рэлея 1708 [5] наступает неустойчивость и появляются конвективные ячейки.
Критическое число Рэлея может быть получено аналитически для ряда различных граничных условий путем проведения анализа возмущений линеаризованных уравнений в устойчивом состоянии. [16] Простейшим случаем является случай двух свободных границ, который лорд Рэлей решил в 1916 году, получив Ra = 27 ⁄ 4 π 4 ≈ 657,51. [17] В случае жесткой границы внизу и свободной границы вверху (как в случае чайника без крышки) критическое число Рэлея получается как Ra = 1100,65. [18]
В случае свободной поверхности жидкости, контактирующей с воздухом, эффекты плавучести и поверхностного натяжения также будут играть роль в том, как развиваются модели конвекции. Жидкости текут из мест с более низким поверхностным натяжением в места с более высоким поверхностным натяжением. Это называется эффектом Марангони . При подаче тепла снизу температура в верхнем слое будет показывать температурные колебания. С повышением температуры поверхностное натяжение уменьшается. Таким образом, будет иметь место боковой поток жидкости на поверхности [19] из более теплых областей в более холодные области. Чтобы сохранить горизонтальную (или почти горизонтальную) поверхность жидкости, более холодная поверхностная жидкость будет опускаться. Это нисходящее движение более холодной жидкости способствует движущей силе конвективных ячеек. Конкретный случай изменений поверхностного натяжения, вызванных градиентом температуры, известен как термокапиллярная конвекция или конвекция Бенара–Марангони.
В 1870 году ирландско-шотландский физик и инженер Джеймс Томсон (1822–1892), старший брат лорда Кельвина , наблюдал за охлаждением воды в ванне; он заметил, что мыльная пленка на поверхности воды была разделена, как если бы поверхность была выложена плиткой (мозаикой). В 1882 году он показал, что мозаичность была вызвана наличием конвективных ячеек. [20] В 1900 году французский физик Анри Бенар независимо пришел к такому же выводу. [21] Эта модель конвекции, эффекты которой обусловлены исключительно градиентом температуры, была впервые успешно проанализирована в 1916 году лордом Рэлеем . [22] Рэлей предположил граничные условия, при которых вертикальная составляющая скорости и возмущение температуры исчезают на верхней и нижней границах (идеальная теплопроводность). Эти предположения привели к тому, что анализ потерял всякую связь с экспериментом Анри Бенара. Это привело к расхождениям между теоретическими и экспериментальными результатами до 1958 года, когда Джон Пирсон (1930– ) переработал проблему на основе поверхностного натяжения. [15] Это то, что первоначально наблюдал Бенар. Тем не менее, в современном использовании «конвекция Рэлея–Бенара» относится к эффектам, вызванным температурой, тогда как «конвекция Бенара–Марангони» относится конкретно к эффектам поверхностного натяжения. [4] Дэвис и Кошмидер предположили, что конвекцию следует по праву называть «конвекцией Пирсона–Бенара». [5]
Конвекцию Рэлея–Бенара также иногда называют «конвекцией Бенара–Рэлея», «конвекцией Бенара» или «конвекцией Рэлея».