машина Мура

Конечный автомат, выходные значения которого определяются только его текущим состоянием

В теории вычислений автомат Мура — это конечный автомат , текущие выходные значения которого определяются только его текущим состоянием . Это контрастирует с автоматом Мили , выходные значения которого определяются как его текущим состоянием, так и значениями его входов. Как и в других конечных автоматах, в автоматах Мура вход обычно влияет на следующее состояние. Таким образом, вход может косвенно влиять на последующие выходы, но не на текущий или немедленный выход. Машина Мура названа в честь Эдварда Ф. Мура , который представил эту концепцию в статье 1956 года « Мысленные эксперименты на последовательных машинах». ^[1]

Формальное определение

Машину Мура можно определить как 6-кортеж, состоящий из следующих элементов: ${\displaystyle (S,s_{0},\Sigma ,O,\delta ,G)}$

• Конечный набор состояний ${\displaystyle S}$
• Начальное состояние (также называемое начальным состоянием), которое является элементом ${\displaystyle s_{0}}$ ${\displaystyle S}$
• Конечный набор, называемый входным алфавитом ${\displaystyle \Sigma }$
• Конечный набор, называемый выходным алфавитом ${\displaystyle O}$
• Функция перехода , отображающая состояние и входной алфавит в следующее состояние ${\displaystyle \delta :S\times \Sigma \rightarrow S}$
• Выходная функция, отображающая каждое состояние в выходной алфавит ${\displaystyle G:S\rightarrow O}$

«Эволюция во времени» реализуется в этой абстракции посредством того, что конечный автомат обращается к изменяющемуся во времени входному символу в дискретные «такты таймера» и реагирует в соответствии со своей внутренней конфигурацией в эти идеализированные моменты, или же посредством того, что конечный автомат ждет следующего входного символа (как в FIFO) и реагирует всякий раз, когда он поступает. ${\displaystyle t_{0},t_{1},t_{2},...}$

Машину Мура можно рассматривать как ограниченный тип конечного преобразователя .

Визуальное представление

Стол

Таблица переходов состояний — это таблица, в которой перечислены все триплеты в отношении перехода . ${\displaystyle \delta :S\times \Sigma \rightarrow S}$

Диаграмма

Диаграмма состояний машины Мура, или диаграмма Мура, представляет собой диаграмму состояний, которая связывает выходное значение с каждым состоянием.

Связь с машинами Мили

Поскольку автоматы Мура и Мили являются типами конечных автоматов, они одинаково выразительны: любой из них может использоваться для синтаксического анализа обычного языка .

Разница между автоматами Мура и автоматами Мили заключается в том, что в последнем выход перехода определяется комбинацией текущего состояния и текущего входа ( как области ), а не только текущим состоянием ( как области ). При представлении в виде диаграммы состояний , ${\displaystyle S\times \Sigma }$ ${\displaystyle G}$ ${\displaystyle S}$ ${\displaystyle G}$

• для машины Мура каждый узел (состояние) помечен выходным значением;
• для автомата Мили каждая дуга (переход) помечена выходным значением.

Каждый автомат Мура эквивалентен автомату Мили с теми же состояниями и переходами, а также выходной функцией , которая берет каждую пару состояние-вход и выдает , где — выходная функция, а — функция перехода. ${\displaystyle M}$ ${\displaystyle G(s,\sigma )=G_{M}(\delta _{M}(s,\sigma ))}$ ${\displaystyle (s,\sigma )}$ ${\displaystyle G_{M}(\delta _{M}(s,\sigma ))}$ ${\displaystyle G_{M}}$ ${\displaystyle M}$ ${\displaystyle \delta _{M}}$ ${\displaystyle M}$

Однако не каждый автомат Мили можно преобразовать в эквивалентный автомат Мура. Некоторые можно преобразовать только в почти эквивалентный автомат Мура, со смещенными во времени выходами. Это связано со способом, которым метки состояний спариваются с метками переходов для формирования пар вход/выход. Рассмотрим переход из состояния в состояние . Вход, вызывающий переход, помечает ребро . Выход, соответствующий этому входу, является меткой состояния . ^[2] Обратите внимание, что это исходное состояние перехода. Таким образом, для каждого входа выход уже зафиксирован до получения входа и зависит исключительно от текущего состояния. Это оригинальное определение Э. Мура. Распространенной ошибкой является использование метки состояния в качестве выхода для перехода . ${\displaystyle s_{i}\rightarrow s_{j}}$ ${\displaystyle s_{i}}$ ${\displaystyle s_{j}}$ ${\displaystyle s_{i}\rightarrow s_{j}}$ ${\displaystyle (s_{i},s_{j})}$ ${\displaystyle s_{i}}$ ${\displaystyle s_{j}}$ ${\displaystyle s_{i}\rightarrow s_{j}}$

Примеры

Типы по количеству входов/выходов.

Простой

Простые машины Мура имеют один вход и один выход:

• детектор краев с использованием XOR
• двоичная счетная машина
• тактовые последовательные системы (ограниченная форма машины Мура, в которой состояние изменяется только при изменении глобального тактового сигнала)

Большинство цифровых электронных систем спроектированы как тактируемые последовательные системы . Тактируемые последовательные системы являются ограниченной формой машины Мура, где состояние изменяется только при изменении глобального тактового сигнала. Обычно текущее состояние хранится в триггерах , а глобальный тактовый сигнал подключен к «тактовому» входу триггеров. Тактируемые последовательные системы являются одним из способов решения проблем метастабильности . Типичная электронная машина Мура включает в себя комбинационную логическую цепь для декодирования текущего состояния в выходы (лямбда). В тот момент, когда текущее состояние изменяется, эти изменения распространяются по этой цепи, и почти мгновенно выход обновляется. Существуют методы проектирования, гарантирующие, что на выходах не возникнет никаких сбоев в течение этого короткого периода, пока эти изменения распространяются по цепи, но большинство систем спроектированы так, что сбои в течение этого короткого переходного времени игнорируются или не имеют значения. Затем выходы остаются неизменными неопределенно долго ( светодиоды остаются яркими, питание остается подключенным к двигателям, соленоиды остаются включенными и т. д.), пока машина Мура снова не изменит состояние.

Машина Мура в комбинационной логике

Рабочий пример

Последовательная сеть имеет один вход и один выход. Выход становится 1 и остается 1 после того, как в качестве входов появились по крайней мере два 0 и две 1.

Пример машины Мура

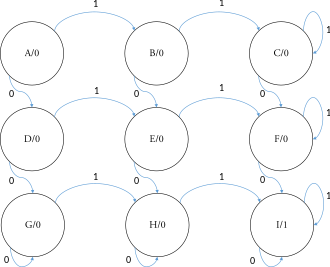
Справа показана машина Мура с девятью состояниями для приведенного выше описания. Начальное состояние — состояние A, а конечное состояние — состояние I. Таблица состояний для этого примера выглядит следующим образом:

Сложный

Более сложные машины Мура могут иметь как несколько входов, так и несколько выходов.

Gedanken-эксперименты

В статье Мура 1956 года " Gedanken-experiments on Sequential Machines", ^[1] автоматы (или машины) определяются как имеющие состояния, входные символы и выходные символы. Доказано девять теорем о структуре и экспериментах с . Позже " машины" стали называться "машинами Мура". ${\displaystyle (n;m;p)}$ ${\displaystyle S}$ ${\displaystyle n}$ ${\displaystyle m}$ ${\displaystyle p}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle S}$

В конце статьи, в разделе «Дополнительные задачи», ставится следующая задача:

Другая непосредственно следующая проблема — улучшение оценок, данных в теоремах 8 и 9.

Теорема Мура 8 формулируется следующим образом:

Если задана произвольная машина , такая, что любые два ее состояния различимы друг от друга, то существует эксперимент длины , который определяет состояние в конце эксперимента. ${\displaystyle (n;m;p)}$ ${\displaystyle S}$ ${\displaystyle {\tfrac {n(n-1)}{2}}}$ ${\displaystyle S}$

В 1957 году А.А. Карацуба доказал следующие две теоремы, которые полностью решили проблему Мура об улучшении границ длины эксперимента его «Теоремы 8».

Теорема А. Если — машина, в которой любые два ее состояния различимы друг от друга, то существует разветвленный эксперимент длиной не более , с помощью которого можно определить состояние в конце эксперимента. ${\displaystyle S}$ ${\displaystyle (n;m;p)}$ ${\displaystyle {\tfrac {(n-1)(n-2)}{2}}+1}$ ${\displaystyle S}$

Теорема B. Существует машина, любые два состояния которой различимы друг от друга, такая, что длина самого короткого эксперимента, устанавливающего состояние машины в конце эксперимента, равна . ${\displaystyle (n;m;p)}$ ${\displaystyle {\tfrac {(n-1)(n-2)}{2}}+1}$

Теоремы А и В легли в основу курсовой работы студента четвертого курса А.А. Карацубы «Об одной задаче из теории автоматов», которая была отмечена благодарственным отзывом на конкурсе студенческих работ механико-математического факультета МГУ в 1958 году. Работа Карацубы была передана в журнал «Успехи математических наук» 17 декабря 1958 года и опубликована там в июне 1960 года. ^[3]

До настоящего времени (2011 г.) результат Карацубы о длительности экспериментов является единственным точным нелинейным результатом как в теории автоматов, так и в схожих задачах теории сложности вычислений .

Смотрите также

• Синхронная цепь
• Машина для помола муки
• Алгоритмическая машина состояний
• Автономная система (математика)

Ссылки

1. Мур, Эдвард Ф. (1956). «Мысленные эксперименты на последовательных машинах». Исследования автоматов, Анналы математических исследований (34). Принстон, Нью-Джерси: Princeton University Press: 129–153.
2. Ли, Эдвард Эшфорд; Сешиа, Санджит Арункумар (2013). Введение во встроенные системы (изд. 1.08). Калифорнийский университет в Беркли: Lulu.com. ISBN 9780557708574. Получено 1 июля 2014 г.
3. Карацуба, А.А. (1960). «Решение одной задачи из теории конечных автоматов». Успехи математических наук (15:3): 157–159.

Дальнейшее чтение

• Conway, JH (1971). Регулярная алгебра и конечные машины . Лондон: Chapman and Hall. ISBN 0-412-10620-5. Збл  0231.94041.
• Мур Э. Ф. Мысленные эксперименты на последовательных машинах. Исследования автоматов, Анналы математических исследований, 34, 129–153. Princeton University Press, Принстон, Нью-Джерси (1956).
• Карацуба А. А. Решение одной задачи из теории конечных автоматов // УМН, 15:3, 157–159 (1960).
• Карацуба А.А. Experimente mit Automaten (нем.) Elektron. Информацияверарб. Кибернетик, 11, 611–612 (1975).
• Карацуба А.А. Список научных трудов .

Машина Мура и Мили

Внешние ссылки

• Медиа, связанные с машиной Мура на Wikimedia Commons