Кооперативное связывание

Молекулярный механизм

Кооперативное связывание происходит в молекулярных системах связывания , содержащих более одного типа или вида молекулы, и в которых один из партнеров не является моновалентным и может связывать более одной молекулы другого вида. В общем, молекулярное связывание представляет собой взаимодействие между молекулами, которое приводит к стабильной физической ассоциации между этими молекулами.

Кооперативное связывание происходит в молекулярной системе связывания, где две или более молекул лиганда могут связываться с молекулой рецептора . Связывание можно считать «кооперативным», если фактическое связывание первой молекулы лиганда с рецептором изменяет сродство связывания второй молекулы лиганда. Связывание молекул лиганда с различными участками на молекуле рецептора не является взаимно независимыми событиями. Кооперативность может быть положительной или отрицательной, что означает, что становится более или менее вероятным, что последующие молекулы лиганда будут связываться с молекулой рецептора.

Кооперативное связывание наблюдается во многих биополимерах, включая белки и нуклеиновые кислоты . Было показано, что кооперативное связывание является механизмом, лежащим в основе большого спектра биохимических и физиологических процессов.

История и математические формализмы

Христиан Бор и концепция кооперативного связывания

В 1904 году Кристиан Бор изучал связывание гемоглобина с кислородом при различных условиях. ^{[1] [2]} При построении графика насыщения гемоглобина кислородом в зависимости от парциального давления кислорода он получил сигмоидальную (или «S-образную») кривую. Это указывает на то, что чем больше кислорода связано с гемоглобином, тем легче большему количеству кислорода связываться — до тех пор, пока все места связывания не будут насыщены. Кроме того, Бор заметил, что увеличение _{давления} CO2 смещает эту кривую вправо — т. е. более высокие концентрации CO2 _{затрудняют} связывание гемоглобина с кислородом. ^[2] Это последнее явление, вместе с наблюдением, что сродство гемоглобина к кислороду увеличивается с ростом pH, известно как эффект Бора .

Оригинальный рисунок Кристиана Бора , показывающий сигмоидальное увеличение оксигемоглобина в зависимости от парциального давления кислорода.

Говорят, что молекула рецептора проявляет кооперативное связывание, если ее связывание с лигандом масштабируется нелинейно с концентрацией лиганда. Кооперативность может быть положительной (если связывание молекулы лиганда увеличивает кажущееся сродство рецептора и, следовательно, увеличивает вероятность связывания другой молекулы лиганда) или отрицательной (если связывание молекулы лиганда уменьшает сродство и, следовательно, делает связывание других молекул лиганда менее вероятным). «Фракционная занятость» рецептора данным лигандом определяется как количество связанных с лигандом участков связывания, деленное на общее количество участков связывания лиганда: ${\displaystyle {\bar {Y}}}$

${\displaystyle {\bar {Y}}={\frac {[{\text{bound sites}}]}{[{\text{bound sites}}]+[{\text{unbound sites}}]}}={\frac {[{\text{bound sites}}]}{[{\text{total sites}}]}}}$

Если , то белок полностью не связан, а если , то он полностью насыщен. Если график при равновесии как функция концентрации лиганда имеет сигмоидальную форму, как это наблюдал Бор для гемоглобина, это указывает на положительную кооперативность. Если это не так, то нельзя сделать никаких утверждений о кооперативности, глядя только на этот график. ${\displaystyle {\bar {Y}}=0}$ ${\displaystyle {\bar {Y}}=1}$ ${\displaystyle {\bar {Y}}}$

Концепция кооперативного связывания применима только к молекулам или комплексам с более чем одним сайтом связывания лиганда. Если существует несколько сайтов связывания лиганда, но связывание лиганда с любым сайтом не влияет на другие, рецептор называется некооперативным. Кооперативность может быть гомотропной , если лиганд влияет на связывание лигандов того же вида, или гетеротропной , если он влияет на связывание других видов лигандов. В случае гемоглобина Бор наблюдал гомотропную положительную кооперативность (связывание кислорода способствует связыванию большего количества кислорода) и гетеротропную отрицательную кооперативность (связывание CO2 _{снижает} способность гемоглобина связывать кислород).

На протяжении 20-го века были разработаны различные структуры для описания связывания лиганда с белком с более чем одним сайтом связывания и кооперативных эффектов, наблюдаемых в этом контексте. ^[3]

Уравнение Хилла

Первое описание кооперативного связывания с многосайтовым белком было разработано А. В. Хиллом . ^[4] Опираясь на наблюдения за связыванием кислорода с гемоглобином и идею о том, что кооперативность возникает из-за агрегации молекул гемоглобина, каждая из которых связывает одну молекулу кислорода, Хилл предложил феноменологическое уравнение, которое с тех пор было названо в его честь :

График Хилла уравнения Хилла показан красным цветом, показывающий наклон кривой, являющейся коэффициентом Хилла, и пересечение с осью x, дающее кажущуюся константу диссоциации. Зеленая линия показывает некооперативную кривую.

${\displaystyle {\bar {Y}}={\frac {K\cdot {}[X]^{n}}{1+K\cdot {}[X]^{n}}}={\frac {[X]^{n}}{K^{*}+[X]^{n}}}={\frac {[X]^{n}}{K_{d}^{n}+[X]^{n}}}}$

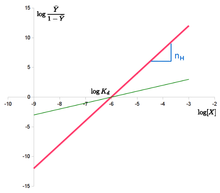
где — «коэффициент Хилла», обозначает концентрацию лиганда, обозначает кажущуюся константу ассоциации (используется в исходной форме уравнения), — эмпирическая константа диссоциации, а — микроскопическая константа диссоциации (используется в современных формах уравнения и эквивалентна ). Если , система проявляет отрицательную кооперативность, тогда как кооперативность положительна, если . Общее число мест связывания лиганда является верхней границей для . Уравнение Хилла можно линеаризировать следующим образом: ${\displaystyle n}$ ${\displaystyle [X]}$ ${\displaystyle K}$ ${\displaystyle K^{*}}$ ${\displaystyle K_{d}}$ ${\displaystyle \mathrm {EC} _{50}}$ ${\displaystyle n<1}$ ${\displaystyle n>1}$ ${\displaystyle n}$

${\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}=n\cdot {}\log[X]-n\cdot {}\log K_{d}}$

«График Хилла» получается путем построения графика зависимости от . В случае уравнения Хилла это линия с наклоном и отсекаемым отрезком . Это означает, что кооперативность предполагается фиксированной, т. е. она не меняется с насыщением. Это также означает, что сайты связывания всегда демонстрируют одинаковое сродство, и кооперативность не возникает из-за сродства, увеличивающегося с концентрацией лиганда. ${\displaystyle \log {\frac {\bar {Y}}{1-{\bar {Y}}}}}$ ${\displaystyle \log[X]}$ ${\displaystyle n_{H}}$ ${\displaystyle n\cdot \log(K_{d})}$

Уравнение Адэра

GS Adair обнаружил, что график Хилла для гемоглобина не является прямой линией, и выдвинул гипотезу, что связывающее сродство не является фиксированным термином, а зависит от насыщения лиганда. ^[5] Продемонстрировав, что гемоглобин содержит четыре гема (и, следовательно, места связывания для кислорода), он исходил из предположения, что полностью насыщенный гемоглобин образуется поэтапно, с промежуточными формами с одной, двумя или тремя связанными молекулами кислорода. Образование каждой промежуточной стадии из несвязанного гемоглобина можно описать с помощью кажущейся макроскопической константы ассоциации . Результирующее дробное заполнение можно выразить как: ${\displaystyle K_{i}}$

${\displaystyle {\bar {Y}}={\frac {1}{4}}\cdot {}{\frac {K_{I}[X]+2K_{II}[X]^{2}+3K_{III}[X]^{3}+4K_{IV}[X]^{4}}{1+K_{I}[X]+K_{II}[X]^{2}+K_{III}[X]^{3}+K_{IV}[X]^{4}}}}$

Или для любого белка с n сайтами связывания лиганда:

${\displaystyle {\bar {Y}}={\frac {1}{n}}{\frac {K_{I}[X]+2K_{II}[X]^{2}+\ldots +nK_{n}[X]^{n}}{1+K_{I}[X]+K_{II}[X]^{2}+\ldots +K_{n}[X]^{n}}}}$

где n обозначает число сайтов связывания, а каждый из них является комбинированной константой ассоциации, описывающей связывание i молекул лиганда. Объединяя обработку Адэра с графиком Хилла, можно прийти к современному экспериментальному определению кооперативности (Хилл, 1985, Абелиович, 2005). Результирующий коэффициент Хилла или, точнее, наклон графика Хилла, рассчитанный по уравнению Адэра, может быть показан как отношение дисперсии числа связывания к дисперсии числа связывания в эквивалентной системе невзаимодействующих сайтов связывания. ^[6] Таким образом, коэффициент Хилла определяет кооперативность как статистическую зависимость одного сайта связывания от состояния другого сайта(ов). ${\displaystyle K_{i}}$

Уравнение Клотца

Работая над кальцийсвязывающими белками, Ирвинг Клотц деконволюционировал константы ассоциации Адайра, рассмотрев поэтапное образование промежуточных стадий, и попытался выразить кооперативное связывание в терминах элементарных процессов, управляемых законом действующих масс. ^{[7] [8]} В его рамках — это константа ассоциации, управляющая связыванием первой молекулы лиганда, константа ассоциации, управляющая связыванием второй молекулы лиганда (когда первая уже связана) и т. д. Для это дает: ${\displaystyle K_{1}}$ ${\displaystyle K_{2}}$ ${\displaystyle {\bar {Y}}}$

${\displaystyle {\bar {Y}}={\frac {1}{n}}{\frac {K_{1}[X]+2K_{1}K_{2}[X]^{2}+\ldots +n\left(K_{1}K_{2}\ldots K_{n}\right)[X]^{n}}{1+K_{1}[X]+K_{1}K_{2}[X]^{2}+\ldots +\left(K_{1}K_{2}\ldots K_{n}\right)[X]^{n}}}}$

Стоит отметить, что константы , и т. д. не относятся к отдельным сайтам связывания. Они описывают, сколько сайтов связывания занято, а не какие именно . Эта форма имеет то преимущество, что кооперативность легко распознается при рассмотрении констант ассоциации. Если все сайты связывания лиганда идентичны с микроскопической константой ассоциации , можно было бы ожидать (то есть ) при отсутствии кооперативности. Мы имеем положительную кооперативность, если лежит выше этих ожидаемых значений для . ${\displaystyle K_{1}}$ ${\displaystyle K_{2}}$ ${\displaystyle K}$ ${\displaystyle K_{1}=nK,K_{2}={\frac {n-1}{2}}K,\ldots K_{n}={\frac {1}{n}}K}$ ${\displaystyle K_{i}={\frac {n-i+1}{i}}K}$ ${\displaystyle K_{i}}$ ${\displaystyle i>1}$

Уравнение Клотца (которое иногда также называют уравнением Адайра-Клотца) до сих пор часто используется в экспериментальной литературе для описания измерений связывания лиганда в терминах последовательных кажущихся констант связывания. ^[9]

Уравнение Полинга

К середине 20-го века возрос интерес к моделям, которые не только описывали бы кривые связывания феноменологически, но и предлагали бы лежащий в их основе биохимический механизм. Лайнус Полинг переосмыслил уравнение, предоставленное Адэром, предположив, что его константы были комбинацией константы связывания для лиганда ( в уравнении ниже) и энергии, поступающей от взаимодействия между субъединицами кооперативного белка ( ниже). ^[10] Полинг фактически вывел несколько уравнений, в зависимости от степени взаимодействия между субъединицами. Основываясь на неверных предположениях о локализации гемов, он выбрал неправильное уравнение для описания связывания кислорода гемоглобином, предположив, что субъединицы расположены в квадрате. Уравнение ниже представляет собой уравнение для тетраэдрической структуры, которое было бы более точным в случае гемоглобина: ${\displaystyle K}$ ${\displaystyle \alpha }$

${\displaystyle {\bar {Y}}={\frac {K[X]+3\alpha {}K^{2}[X]^{2}+3\alpha {}^{3}K^{3}[X]^{3}+\alpha {}^{6}K^{4}[X]^{4}}{1+4K[X]+6\alpha {}K^{2}[X]^{2}+4\alpha {}^{3}K^{3}[X]^{3}+\alpha {}^{6}K^{4}[X]^{4}}}}$

Модель КНФ

Основываясь на результатах, показывающих, что структура кооперативных белков изменяется при связывании с их лигандом, Дэниел Кошланд и коллеги ^[11] уточнили биохимическое объяснение механизма, описанного Полингом. ^[10] Модель Кошланда-Немети-Филмера (KNF) предполагает, что каждая субъединица может существовать в одной из двух конформаций: активной или неактивной. Связывание лиганда с одной субъединицей вызовет немедленное конформационное изменение этой субъединицы из неактивной в активную конформацию, механизм, описанный как «индуцированное соответствие». ^[12] Кооперативность, согласно модели KNF, возникает из-за взаимодействий между субъединицами, сила которых варьируется в зависимости от относительных конформаций вовлеченных субъединиц. Для тетраэдрической структуры (они также рассматривали линейные и квадратные структуры) они предложили следующую формулу:

${\displaystyle {\bar {Y}}={\frac {K_{AB}^{3}(K_{X}K_{t}[X])+3K_{AB}^{4}K_{BB}(K_{X}K_{t}[X])^{2}+3K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t}[X])^{3}+K_{BB}^{6}(K_{X}K_{t}[X])^{4}}{1+4K_{AB}^{3}(K_{X}K_{t}[X])+6K_{AB}^{4}K_{BB}(K_{X}K_{t}[X])^{2}+4K_{AB}^{3}K_{BB}^{3}(K_{X}K_{t}[X])^{3}+K_{BB}^{6}(K_{X}K_{t}[X])^{4}}}}$

Где — константа ассоциации для X, — отношение состояний B и A в отсутствие лиганда («переход»), а — относительные стабильности пар соседних субъединиц по сравнению с парой, в которой обе субъединицы находятся в состоянии A (обратите внимание, что в статье KNF фактически представлено число занятых участков, которое здесь умножено на 4 ). ${\displaystyle K_{X}}$ ${\displaystyle K_{t}}$ ${\displaystyle K_{AB}}$ ${\displaystyle K_{BB}}$ ${\displaystyle N_{s}}$ ${\displaystyle {\bar {Y}}}$

Модель MWC

Схема реакции модели Моно-Ваймана-Шанжо белка, состоящего из двух протомеров. Протомер может существовать в двух состояниях, каждое из которых имеет различное сродство к лиганду. L — отношение состояний в отсутствие лиганда, c — отношение сродств.

Энергетическая диаграмма модели Моно-Ваймана-Шанжо белка, состоящего из двух протомеров. Большее сродство лиганда к состоянию R означает, что последнее преимущественно стабилизируется связыванием.

Модель Моно-Ваймана-Шанжо (MWC) для согласованных аллостерических переходов ^[13] пошла на шаг дальше, исследуя кооперативность на основе термодинамики и трехмерных конформаций. Первоначально она была сформулирована для олигомерных белков с симметрично расположенными идентичными субъединицами, каждая из которых имеет один сайт связывания лиганда. Согласно этой структуре, два (или более) взаимопревращаемых конформационных состояния аллостерического белка сосуществуют в тепловом равновесии. Состояния, часто называемые напряженными (T) и расслабленными (R), различаются по сродству к молекуле лиганда. Соотношение между двумя состояниями регулируется связыванием молекул лиганда, которое стабилизирует состояние с более высоким сродством. Важно, что все субъединицы молекулы изменяют состояния одновременно, явление, известное как «согласованный переход».

Константа аллостерической изомеризации L описывает равновесие между обоими состояниями, когда не связана ни одна молекула лиганда: . Если L очень велико, большая часть белка находится в состоянии T в отсутствие лиганда. Если L мало (близко к единице), состояние R почти так же заселено, как и состояние T. Отношение констант диссоциации лиганда из состояний T и R описывается константой c : . Если , то оба состояния R и T имеют одинаковое сродство к лиганду, и лиганд не влияет на изомеризацию. Значение c также указывает, насколько сильно изменяется равновесие между состояниями T и R при связывании лиганда: чем меньше c , тем больше равновесие смещается в сторону состояния R после одного связывания. При дробная заселенность описывается как: ${\displaystyle L={\frac {\left[T_{0}\right]}{\left[R_{0}\right]}}}$ ${\displaystyle c={\frac {K_{d}^{R}}{K_{d}^{T}}}}$ ${\displaystyle c=1}$ ${\displaystyle \alpha ={\frac {[X]}{K_{d}^{R}}}}$

${\displaystyle {\bar {Y}}={\frac {\alpha (1+\alpha )^{n-1}+Lc\alpha (1+c\alpha )^{n-1}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}$

Сигмоидальный график Хилла аллостерических белков затем может быть проанализирован как прогрессивный переход от состояния T (низкое сродство) к состоянию R (высокое сродство) по мере увеличения насыщения. Наклон графика Хилла также зависит от насыщения, с максимальным значением в точке перегиба. Пересечения между двумя асимптотами и осью Y позволяют определить сродство обоих состояний к лиганду.

График Хилла функции связывания MWC красным цветом, чистого состояния T и R зеленым цветом. По мере смещения конформации от T к R изменяется и функция связывания. Пересечения с осью x дают кажущуюся константу диссоциации, а также микроскопические константы диссоциации состояний R и T.

В белках конформационные изменения часто связаны с активностью или активностью по отношению к определенным целям. Такая активность часто является физиологически значимой или экспериментально измеряемой. Степень конформационных изменений описывается функцией состояния , которая обозначает долю белка, присутствующего в состоянии. Как показывает энергетическая диаграмма, увеличивается по мере связывания большего количества молекул лиганда. Выражение для имеет вид: ${\displaystyle {\bar {R}}}$ ${\displaystyle R}$ ${\displaystyle {\bar {R}}}$ ${\displaystyle {\bar {R}}}$

${\displaystyle {\bar {R}}={\frac {(1+\alpha )^{n}}{(1+\alpha )^{n}+L(1+c\alpha )^{n}}}}$

Важнейшим аспектом модели MWC является то, что кривые для и не совпадают, ^[14] т.е. фракционное насыщение не является прямым индикатором конформационного состояния (и, следовательно, активности). Более того, степени кооперативности связывания и кооперативности активации могут быть очень разными: экстремальный случай обеспечивается жгутиковым двигателем бактерий с коэффициентом Хилла 1,7 для связывания и 10,3 для активации. ^{[15] [16]} Сверхлинейность ответа иногда называют сверхчувствительностью . ${\displaystyle {\bar {Y}}}$ ${\displaystyle {\bar {R}}}$

Если аллостерический белок связывается с мишенью, которая также имеет более высокое сродство к состоянию R, то связывание с мишенью дополнительно стабилизирует состояние R, тем самым увеличивая сродство лиганда. Если, с другой стороны, мишень преимущественно связывается с состоянием T, то связывание с мишенью будет иметь отрицательный эффект на сродство лиганда. Такие мишени называются аллостерическими модуляторами .

С момента своего создания структура MWC была расширена и обобщена. Были предложены вариации, например, для обслуживания белков с более чем двумя состояниями, ^[17] белков, которые связываются с несколькими типами лигандов ^{[18] [19]} или несколькими типами аллостерических модуляторов ^[19] и белков с неидентичными субъединицами или сайтами связывания лигандов. ^[20]

Примеры

Список молекулярных ансамблей, демонстрирующих кооперативное связывание лигандов, очень велик, но некоторые примеры особенно примечательны своим историческим интересом, необычными свойствами или физиологической значимостью.

Мультяшное изображение белка гемоглобина в двух его конформациях: «напряженная (T)» слева, соответствующая дезокси-форме (получена из PDB id:11LFL), и «расслабленная (R)» справа, соответствующая окси-форме (получена из PDB id:1LFT).

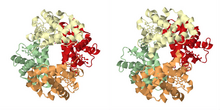
Как описано в историческом разделе, наиболее известным примером кооперативного связывания является гемоглобин . Его четвертичная структура, решенная Максом Перуцем с помощью рентгеновской дифракции, ^[21] демонстрирует псевдосимметричный тетраэдр, несущий четыре центра связывания (гема) для кислорода. Многие другие молекулярные ансамбли, демонстрирующие кооперативное связывание, были изучены очень подробно.

Мультимерные ферменты

Активность многих ферментов регулируется аллостерическими эффекторами. Некоторые из этих ферментов являются мультимерными и несут несколько участков связывания для регуляторов.

Треониндезаминаза была одним из первых ферментов, предположительно ведущих себя подобно гемоглобину ^[22] и связывающих лиганды кооперативно. ^[23] Позднее было показано, что она является тетрамерным белком. ^[24]

Другим ферментом, который, как было ранее предложено, кооперативно связывает лиганды, является аспартат-транс-карбамилаза . ^[25] Хотя первоначальные модели соответствовали четырем сайтам связывания, ^{[26] позднее} Уильям Липскомб и его коллеги показали, что его структура является гексамерной . ^[27]

Ионные каналы

Большинство ионных каналов образованы несколькими идентичными или псевдоидентичными мономерами или доменами, расположенными симметрично в биологических мембранах. Несколько классов таких каналов, открытие которых регулируется лигандами, демонстрируют кооперативное связывание этих лигандов.

Еще в 1967 году ^[28] (когда точная природа этих каналов была еще неизвестна) было высказано предположение, что никотиновые ацетилхолиновые рецепторы связывают ацетилхолин кооперативным образом из-за существования нескольких участков связывания. Очистка рецептора ^[29] и его характеристика продемонстрировали пентамерную структуру с участками связывания, расположенными на интерфейсах между субъединицами, что подтверждается структурой домена связывания рецептора. ^[30]

Рецепторы инозитолтрифосфата (IP3) образуют другой класс лиганд-управляемых ионных каналов, демонстрирующих кооперативное связывание. ^[31] Структура этих рецепторов показывает четыре симметрично расположенных участка связывания IP3. ^[32]

Многосайтовые молекулы

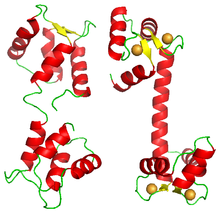
Хотя большинство белков, демонстрирующих кооперативное связывание, представляют собой мультимерные комплексы гомологичных субъединиц, некоторые белки несут несколько участков связывания для одного и того же лиганда на одном и том же полипептиде. Одним из таких примеров является кальмодулин . Одна молекула кальмодулина кооперативно связывает четыре иона кальция. ^[33] Его структура представляет четыре домена EF-hand , ^[34] каждый из которых связывает один ион кальция. Молекула не демонстрирует квадратную или тетраэдрическую структуру, а образована двумя долями, каждая из которых несет два домена EF-hand.

Карикатурное изображение белка кальмодулина в двух его конформациях: «закрытая» слева (получено из PDB id: 1CFD) и «открытая» справа (получено из PDB id: 3CLN). Открытая конформация представлена ​​связанной с 4 ионами кальция (оранжевые сферы).

Факторы транскрипции

Также было показано кооперативное связывание белков с нуклеиновыми кислотами. Классическим примером является связывание репрессора фага лямбда с его операторами, которое происходит кооперативно. ^{[35] [36]} Другие примеры факторов транскрипции демонстрируют положительную кооперативность при связывании со своей целью, например, репрессор насосов TtgABC ^[37] (n=1,6), а также условную кооперативность, проявляемую факторами транскрипции HOXA11 и FOXO1 . ^[38]

Напротив, были также зарегистрированы примеры отрицательной кооперативности для связывания факторов транскрипции, как для гомодимерного репрессора оперона гидроксилазы цитохрома P450cam Pseudomonas putida ^[39] (n=0,56).

Конформационное распространение и кооперативность связывания

Ранее утверждалось, что некоторые белки, особенно те, которые состоят из многих субъединиц, могут регулироваться обобщенным механизмом MWC, в котором переход между состояниями R и T не обязательно синхронизирован по всему белку. ^[40] В 1969 году Уайман ^[41] предложил такую ​​модель со «смешанными конформациями» (т. е. некоторые протомеры в состоянии R, некоторые в состоянии T) для дыхательных белков беспозвоночных.

Следуя схожей идее, модель конформационного распространения Дьюка и коллег ^[42] включает как модель KNF, так и модель MWC как особые случаи. В этой модели субъединица не меняет конформацию автоматически при связывании лиганда (как в модели KNF), и все субъединицы в комплексе не меняют конформации вместе (как в модели MWC). Конформационные изменения являются стохастическими с вероятностью переключения состояний субъединицы в зависимости от того, связана ли она с лигандом или нет, и от конформационного состояния соседних субъединиц. Таким образом, конформационные состояния могут «распространяться» по всему комплексу.

Влияние компонентов, расположенных выше и ниже по потоку, на сверхчувствительность модуля

В живой клетке сверхчувствительные модули встроены в большую сеть с восходящими и нисходящими компонентами. Эти компоненты могут ограничивать диапазон входов, которые модуль будет получать, а также диапазон выходов модуля, которые сеть сможет обнаружить. ^[43] Чувствительность модульной системы зависит от этих ограничений. Ограничения динамического диапазона, накладываемые нисходящими компонентами, могут производить эффективную чувствительность, намного большую, чем у исходного модуля, если рассматривать его изолированно.

Ссылки

Эта статья была адаптирована из следующего источника по лицензии CC BY 4.0 (2013) (отчеты рецензента): Melanie I Stefan; Nicolas Le Novère (2013). "Cooperative binding". PLOS Computational Biology . 9 (6): e1003106. doi : 10.1371/JOURNAL.PCBI.1003106 . ISSN  1553-734X. PMC 3699289.  PMID 23843752.  Wikidata Q21045427  .

1. Бор C (1904). «Die Sauerstoffaufnahme des originalen Blutfarbstoffes und des aus dem Blute dargestellten Hämoglobins». Централблатт Физиол. (на немецком языке). 23 : 688–690.
2. Бор C, Хассельбальх К , Крог А (1904). «Ueber einen in biologischer Beziehung wichtigen Einfluss, den die Kohlensäurespannung des Blutes auf dessen Sauerstoffbindung übt». Скандинавский архив физиологии . 16 (2): 402–412. дои : 10.1111/j.1748-1716.1904.tb01382.x .
3. Wyman J, Gill SJ (1990). Связывание и сцепление. Функциональная химия биологических молекул . Mill Valley: University Science Books.
4. Хилл AV (1910). «Возможные эффекты агрегации молекул гемоглобина на кривые его диссоциации». J Physiol . 40 : iv–vii.
5. Adair GS (1925). «Система гемоглобина. IV. Кривая диссоциации кислорода гемоглобина». J Biol Chem . 63 (2): 529–545. doi : 10.1016/S0021-9258(18)85018-9 .
6. Абелиович Х (июль 2005 г.). «Эмпирический экстремальный принцип для коэффициента Хилла во взаимодействиях лиганд-белок, показывающий отрицательную кооперативность». Biophysical Journal . 89 (1): 76–9. Bibcode :2005BpJ....89...76A. doi :10.1529/biophysj.105.060194. PMC 1366580 . PMID  15834004. 
7. Klotz IM (январь 1946). «Применение закона действия масс к связыванию белками; взаимодействие с кальцием». Архивы биохимии . 9 : 109–117. PMID  21009581.
8. Klotz IM (январь 2004). «Комплексы лиганд-рецептор: происхождение и развитие концепции». Журнал биологической химии . 279 (1): 1–12. doi : 10.1074/jbc.X300006200 . PMID  14604979.
9. Dagher R, Peng S, Gioria S, Fève M, Zeniou M, Zimmermann M, Pigault C, Haiech J, Kilhoffer MC (май 2011 г.). «Общая стратегия для характеристики комплексов кальмодулин-кальций, участвующих в распознавании мишени CaM: домены связывания кальмодулина DAPK и EGFR взаимодействуют с различными комплексами кальмодулин-кальций». Biochimica et Biophysica Acta (BBA) - Molecular Cell Research . 1813 (5): 1059–67. doi : 10.1016/j.bbamcr.2010.11.004 . PMID  21115073.
10. Pauling L (апрель 1935 г.). «Кислородное равновесие гемоглобина и его структурная интерпретация». Труды Национальной академии наук Соединенных Штатов Америки . 21 (4): 186–91. Bibcode :1935PNAS...21..186P. doi : 10.1073/pnas.21.4.186 . PMC 1076562 . PMID  16587956. 
11. Koshland DE, Némethy G, Filmer D (январь 1966). «Сравнение экспериментальных данных по связыванию и теоретических моделей в белках, содержащих субъединицы». Биохимия . 5 (1): 365–85. doi :10.1021/bi00865a047. PMID  5938952.
12. Koshland DE (февраль 1958). «Применение теории специфичности ферментов к синтезу белков». Труды Национальной академии наук Соединенных Штатов Америки . 44 (2): 98–104. Bibcode : 1958PNAS... 44 ...98K. doi : 10.1073/pnas.44.2.98 . PMC 335371. PMID  16590179. 
13. Monod J, Wyman J, Changeux JP (май 1965). «О природе аллостерических переходов: правдоподобная модель». Журнал молекулярной биологии . 12 : 88–118. doi :10.1016/S0022-2836(65)80285-6. PMID  14343300.
14. Rubin MM, Changeux JP (ноябрь 1966 г.). «О природе аллостерических переходов: последствия неисключительного связывания лигандов». Журнал молекулярной биологии . 21 (2): 265–74. doi :10.1016/0022-2836(66)90097-0. PMID  5972463.
15. Cluzel P, Surette M, Leibler S (март 2000 г.). «Сверхчувствительный бактериальный двигатель, обнаруженный путем мониторинга сигнальных белков в отдельных клетках». Science . 287 (5458): 1652–5. Bibcode :2000Sci...287.1652C. doi :10.1126/science.287.5458.1652. PMID  10698740.
16. Sourjik V, Berg HC (октябрь 2002 г.). «Связывание регулятора реакции Escherichia coli CheY с его мишенью, измеренное in vivo с помощью переноса энергии резонанса флуоресценции». Труды Национальной академии наук Соединенных Штатов Америки . 99 (20): 12669–74. Bibcode : 2002PNAS...9912669S. doi : 10.1073 /pnas.192463199 . PMC 130518. PMID  12232047. 
17. Edelstein SJ, Schaad O, Henry E, Bertrand D, Changeux JP (ноябрь 1996 г.). «Кинетический механизм для никотиновых ацетилхолиновых рецепторов на основе множественных аллостерических переходов». Biological Cybernetics . 75 (5): 361–79. CiteSeerX 10.1.1.17.3066 . doi :10.1007/s004220050302. PMID  8983160. S2CID  6240168. 
18. Mello BA, Tu Y (ноябрь 2005 г.). «Аллостерическая модель для гетерогенных рецепторных комплексов: понимание бактериальных хемотаксических ответов на множественные стимулы». Труды Национальной академии наук Соединенных Штатов Америки . 102 (48): 17354–9. Bibcode : 2005PNAS..10217354M. doi : 10.1073/pnas.0506961102 . PMC 1297673. PMID  16293695. 
19. Najdi TS, Yang CR, Shapiro BE, Hatfield GW, Mjolsness ED (апрель 2006 г.). «Применение обобщенной модели MWC для математического моделирования метаболических путей, регулируемых аллостерическими ферментами». Журнал биоинформатики и вычислительной биологии . 4 (2): 335–55. CiteSeerX 10.1.1.121.9382 . doi :10.1142/S0219720006001862. PMID  16819787. 
20. Стефан MI, Эдельштейн SJ, Ле Новер N (июль 2009 г.). «Вычисление феноменологических констант Адэра-Клотца из микроскопических параметров MWC». BMC Systems Biology . 3 : 68. doi : 10.1186/1752-0509-3-68 . PMC 2732593 . PMID  19602261. 
21. Perutz MF, Rossmann MG, Cullis AF, Muirhead H, Will G, North AC (февраль 1960). "Структура гемоглобина: трехмерный синтез Фурье с разрешением 5,5 А., полученный с помощью рентгеновского анализа". Nature . 185 (4711): 416–22. Bibcode :1960Natur.185..416P. doi :10.1038/185416a0. PMID  18990801. S2CID  4208282.
22. Changeux JP (1961). «Механизмы управления обратной связью биосинтетической L-треониндезаминазы L-изолейцином». Симпозиумы по количественной биологии в Колд-Спринг-Харбор . 26 : 313–8. doi :10.1101/SQB.1961.026.01.037. PMID  13878122.
23. Шанже, Ж.-П. (1963).«Аллостерические взаимодействия в биосинтетической L-треониндезаминазе из E. coli K12». Cold Spring Harb Symp Quant Biol . 28 : 497–504. doi :10.1101/sqb.1963.028.01.066.
24. Gallagher DT, Gilliland GL, Xiao G, Zondlo J, Fisher KE, Chinchilla D, Eisenstein E (апрель 1998 г.). «Структура и контроль пиридоксальфосфатзависимой аллостерической треониндезаминазы». Структура . 6 (4): 465–75. doi : 10.1016/s0969-2126(98)00048-3 . PMID  9562556.
25. Gerhart JC, Pardee AB (март 1962). «Энзимология контроля с помощью ингибирования по принципу обратной связи». Журнал биологической химии . 237 (3): 891–6. doi : 10.1016/S0021-9258(18)60389-8 . PMID  13897943.
26. Changeux JP, Rubin MM (февраль 1968). «Аллостерические взаимодействия в аспартаттранскарбамилазе. 3. Интерпретация экспериментальных данных в терминах модели Моно, Ваймана и Changeux». Биохимия . 7 (2): 553–61. doi :10.1021/bi00842a601. PMID  4868541.
27. Honzatko RB, Crawford JL, Monaco HL, Ladner JE, Ewards BF, Evans DR, Warren SG, Wiley DC, Ladner RC, Lipscomb WN (сентябрь 1982 г.). «Кристаллические и молекулярные структуры нативной и связанной с CTP аспартаткарбамоилтрансферазы из Escherichia coli». Журнал молекулярной биологии . 160 (2): 219–63. doi :10.1016/0022-2836(82)90175-9. PMID  6757446.
28. Карлин А. (август 1967 г.). «О применении «правдоподобной модели» аллостерических белков к рецептору ацетилхолина». Журнал теоретической биологии . 16 (2): 306–20. Bibcode : 1967JThBi..16..306K. doi : 10.1016/0022-5193(67)90011-2. PMID  6048545.
29. Changeux JP, Kasai M, Lee CY (ноябрь 1970 г.). «Использование токсина змеиного яда для характеристики белка холинергического рецептора». Труды Национальной академии наук Соединенных Штатов Америки . 67 (3): 1241–7. Bibcode : 1970PNAS...67.1241C. doi : 10.1073/pnas.67.3.1241 . PMC 283343. PMID  5274453 . 
30. Брейк К., ван Дейк В.Дж., Клаассен Р.В., Шуурманс М., ван дер Ост Дж., Смит AB, Sixma TK (май 2001 г.). «Кристаллическая структура ACh-связывающего белка обнаруживает лиганд-связывающий домен никотиновых рецепторов». Природа . 411 (6835): 269–76. Бибкод : 2001Natur.411..269B. дои : 10.1038/35077011. PMID  11357122. S2CID  4415937.
31. Meyer T, Holowka D, Stryer L (апрель 1988). «Высоко кооперативное открытие кальциевых каналов инозитол-1,4,5-трифосфатом». Science . 240 (4852): 653–6. Bibcode :1988Sci...240..653M. doi :10.1126/science.2452482. PMID  2452482.
32. Seo MD, Velamakanni S, Ishiyama N, Stathopulos PB, Rossi AM, Khan SA, Dale P, Li C, Ames JB, Ikura M, Taylor CW (январь 2012 г.). «Структурная и функциональная консервация ключевых доменов в рецепторах InsP3 и рианодина». Nature . 483 (7387): 108–12. Bibcode :2012Natur.483..108S. doi :10.1038/nature10751. PMC 3378505 . PMID  22286060. 
33. Teo TS, Wang JH (сентябрь 1973 г.). «Механизм активации циклической аденозиновой 3':5'-монофосфатной фосфодиэстеразы из бычьего сердца ионами кальция. Идентификация активатора белка как белка, связывающего Ca2+». Журнал биологической химии . 248 (17): 5950–5. doi : 10.1016/S0021-9258(19)43493-5 . PMID  4353626.
34. Babu YS, Sack JS, Greenhough TJ, Bugg CE, Means AR, Cook WJ (1985). «Трехмерная структура кальмодулина». Nature . 315 (6014): 37–40. Bibcode :1985Natur.315...37B. doi :10.1038/315037a0. PMID  3990807. S2CID  4316112.
35. Ptashne M, Jeffrey A, Johnson AD, Maurer R, Meyer BJ, Pabo CO, Roberts TM, Sauer RT (январь 1980 г.). «Как работают лямбда-репрессор и cro». Cell . 19 (1): 1–11. doi :10.1016/0092-8674(80)90383-9. PMID  6444544. S2CID  54281357.
36. Ackers GK, Johnson AD, Shea MA (февраль 1982 г.). «Количественная модель регуляции генов репрессором фага лямбда». Труды Национальной академии наук Соединенных Штатов Америки . 79 (4): 1129–33. Bibcode : 1982PNAS...79.1129A. doi : 10.1073/pnas.79.4.1129 . PMC 345914. PMID  6461856 . 
37. Крелл Т., Теран В., Майорга О.Л., Ривас Г., Хименес М., Дэниелс С., Молина-Энарес А.Дж., Мартинес-Буэно М., Гальегос М.Т., Рамос Х.Л. (июнь 2007 г.). «Оптимизация палиндромного порядка оператора TtgR повышает кооперативность связывания». Журнал молекулярной биологии . 369 (5): 1188–99. дои : 10.1016/j.jmb.2007.04.025. ПМИД  17498746.
38. Nnamani, Mauris C.; et al. (2016). «Производный аллостерический переключатель лежит в основе эволюции условной кооперативности между HOXA11 и FOXO1». Cell Reports . 15 (10): 2097–2108. doi : 10.1016/j.celrep.2016.04.088 . hdl : 2437/230273 . PMID  27239043.
39. Aramaki H, Kabata H, Takeda S, Itou H, Nakayama H, Shimamoto N (декабрь 2011 г.). «Формирование тройного комплекса репрессор-индуктор-оператор: отрицательная кооперативность связывания d-камфоры с CamR». Genes to Cells . 16 (12): 1200–7. doi : 10.1111/j.1365-2443.2011.01563.x . PMID  22093184. S2CID  29006987.
40. Changeux JP, Thiéry J, Tung Y, Kittel C (февраль 1967 г.). «О кооперативности биологических мембран». Труды Национальной академии наук Соединенных Штатов Америки . 57 (2): 335–41. Bibcode :1967PNAS...57..335C. doi : 10.1073/pnas.57.2.335 . PMC 335510 . PMID  16591474. 
41. Wyman J (февраль 1969). «Возможные аллостерические эффекты в расширенных биологических системах». Журнал молекулярной биологии . 39 (3): 523–38. doi :10.1016/0022-2836(69)90142-9. PMID  5357210.
42. Duke TA, Le Novère N, Bray D (май 2001). «Конформационное распространение в кольце белков: стохастический подход к аллостерии». Журнал молекулярной биологии . 308 (3): 541–53. doi :10.1006/jmbi.2001.4610. PMID  11327786. S2CID  14914075.
43. Altszyler E, Ventura A, Colman-Lerner A, Chernomoretz A (октябрь 2014 г.). «Влияние ограничений восходящего и нисходящего потоков на сверхчувствительность сигнального модуля». Physical Biology . 11 (6): 066003. Bibcode :2014PhBio..11f6003A. doi :10.1088/1478-3975/11/6/066003. PMC 4233326 . PMID  25313165.